Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T13:20:58.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Fundamentals of laminar free convection in internally heated fluids at values of the Rayleigh–Roberts number up to 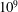$10^{9}$

Published online by Cambridge University Press:  11 May 2018

Kenny Vilella Open the ORCID record for Kenny Vilella [Opens in a new window] ,
Angela Limare ,
Claude Jaupart ,
Cinzia G. Farnetani ,
Loic Fourel  and
Edouard Kaminski
Kenny Vilella*
Affiliation:
Institut de Physique du Globe, Univ. Paris Diderot, Sorbonne Paris Cité, CNRS, F-75005 Paris, France Institute of Earth Sciences, Academia Sinica, Taipei 11529, Taiwan
Angela Limare
Affiliation:
Institut de Physique du Globe, Univ. Paris Diderot, Sorbonne Paris Cité, CNRS, F-75005 Paris, France
Claude Jaupart
Affiliation:
Institut de Physique du Globe, Univ. Paris Diderot, Sorbonne Paris Cité, CNRS, F-75005 Paris, France
Cinzia G. Farnetani
Affiliation:
Institut de Physique du Globe, Univ. Paris Diderot, Sorbonne Paris Cité, CNRS, F-75005 Paris, France
Loic Fourel
Affiliation:
Institut de Physique du Globe, Univ. Paris Diderot, Sorbonne Paris Cité, CNRS, F-75005 Paris, France Geological Survey of Norway, 7040 Trondheim, Norway
Edouard Kaminski
Affiliation:
Institut de Physique du Globe, Univ. Paris Diderot, Sorbonne Paris Cité, CNRS, F-75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Motions in the solid mantle of silicate planets are predominantly driven by internal heat sources and occur in laminar regimes that have not been systematically investigated. Using high-resolution numerical simulations conducted in three dimensions for a large range of Rayleigh–Roberts numbers ( 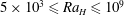$5\times 10^{3}\leqslant Ra_{H}\leqslant 10^{9}$ ), we have determined the characteristics of flow in internally heated fluid layers with both rigid and free slip boundaries. Superficial planforms evolve with increasing $Ra_{H}$ from a steady-state tessellation of hexagonal cells with axial downwellings to time-dependent clusters of thin linear downwellings within large areas of nearly isothermal fluid. The transition between the two types of planforms occurs as a remarkable flow polarity reversal over a small 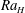$Ra_{H}$ range, such that downwellings go from isolated cylindrical structures encircled by upwellings to thin interconnected linear segments outlining polygonal cells. In time-dependent regimes at large values of 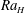$Ra_{H}$ , linear downwellings dominate the flow field at shallow depth but split and merge at intermediate depths into nearly cylindrical plume-like structures that go through the whole layer. With increasing 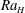$Ra_{H}$ , the number of plumes per unit area and their velocities increase whilst the amplitude of thermal anomalies decreases. Scaling laws for the main flow characteristics are derived for 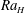$Ra_{H}$ values in a 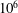$10^{6}$ – $10^{9}$ range. For given 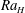$Ra_{H}$ , plumes are significantly colder, narrower and wider apart beneath free boundaries than beneath rigid ones. From the perspective of planetary studies, these results alert to the dramatic changes of convective planform that can occur along secular cooling.

JFM classification

Convection: Convection Nonlinear Dynamical Systems: Pattern formation Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 966 - 998
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Ferreira, R. T. D. S. & Boberg, T. 1986 Turbulent thermal convection in wide horizontal fluid layers. Exp. Fluids 4 (3), 121–141.CrossRefGoogle Scholar
Batchelor, G. K. 1954 Heat convection and buoyancy effects in fluids. Q. J. R. Meteorol. Soc. 80, 339–358.Google Scholar
Bello, L., Coltice, N., Rolf, T. & Tackley, P. J. 2014 On the predictability limit of convection models of the Earth’s mantle. Geochem. Geophys. Geosyst. 15, 2319–2328.Google Scholar
Boussinesq, J. 1903 Théorie analytique de la chaleur mise en harmonie avec la thermodynamique et avec la théorie mécanique de la lumière, Tome II. Gauthier-Villars.Google Scholar
Carrigan, C. R. 1982 Multiple-scale convection in the Earth’s mantle: a three-dimensional study. Science 215, 965–967.CrossRefGoogle Scholar
Carrigan, C. R. 1985 Convection in an internally heated, high Prandtl number fluid: a laboratory study. Geophys. Astrophys. Fluid Dyn. 32, 1–21.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X. Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Cheung, F. B. 1977 Natural convection in a volumetrically heated fluid layer at high Rayleigh numbers. Intl J. Heat Mass Transfer 20, 499–506.Google Scholar
Ching, E. S. C., Guo, H., Shang, X. D., Tong, P. & Xia, K. Q. 2004 Extraction of plumes in turbulent thermal convection. Phys. Rev. Lett. 93 (12), 124501.Google Scholar
Christensen, U. R. & Hofmann, A. W. 1994 Segregation of subducted oceanic crust in the convecting mantle. J. Geophys. Res. 99, 19867–19884.Google Scholar
Cottaar, S. & Buffett, B. 2012 Convection in the Earth’s inner core. Phys. Earth Planet. Inter. 198, 67–78.Google Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851–1112.Google Scholar
Davaille, A. & Limare, A. 2015 Laboratory studies of mantle convection. In Treatise on Geophysics, vol. 7, pp. 73–144. Elsevier.CrossRefGoogle Scholar
Deschamps, F., Rogister, Y. & Tackley, P. J. 2018 Constraints on core-mantle boundary topography from models of thermal and thermo-chemical convection. Geophys. J. Intl 212, 164–188.CrossRefGoogle Scholar
Deschamps, F. & Tackley, P. J. 2008 Searching for models of thermo-chemical convection that explain probabilistic tomography. Part I. Principles and influence of rheological parameters. Phys. Earth Planet. Inter. 171, 357–373.Google Scholar
Deschamps, F. & Tackley, P. J. 2009 Searching for models of thermo-chemical convection that explain probabilistic tomography. Part II. Influence of physical and compositional parameters. Phys. Earth Planet. Inter. 176, 1–18.Google Scholar
Galsa, A. & Lenkey, L. 2007 Quantitative investigation of physical properties of mantle plumes in three-dimensional numerical models. Phys. Fluids 19, 116601.Google Scholar
Glover, G. M. C. & Generalis, S. C. 2009 Pattern competition in homogeneously heated fluid layers. Engng Appl. Comput. Fluid Mech. 3, 164–174.Google Scholar
Goluskin, D. 2015 Internally Heated Convection and Rayleigh–Bénard Convection. Springer International Publishing.Google Scholar
Goluskin, D. & Spiegel, E. A. 2012 Convection driven by internal heating. Phys. Lett. A 377, 83–92.Google Scholar
Gomi, H., Ohta, K., Hirose, K., Labrosse, S., Caracas, R., Verstraete, M. J. & Hernlund, J. W. 2013 The high conductivity of iron and thermal evolution of the Earth’s core. Phys. Earth Planet. Inter. 224, 88–103.Google Scholar
Guillou, L. & Jaupart, C. 1995 On the effect of continents on mantle convection. J. Geophys. Res. 100 (B12), 24217–24238.CrossRefGoogle Scholar
Gurnis, M. 1988 Large-scale mantle convection and the aggregation and dispersal of supercontinents. Nature 332 (6166), 695–699.Google Scholar
Houseman, G. 1988 The dependence of convection planform on mode of heating. Nature 332, 346–349.Google Scholar
Hussmann, H., Choblet, G., Lainey, V., Matson, D. L., Sotin, C., Tobie, G. & Van Hoolst, T. 2010 Implications of rotation, orbital states, energy sources, and heat transport for internal processes in icy satellites. Space Sci. Rev. 153, 314–348.Google Scholar
Ichikawa, H., Kurita, K., Yamagishi, Y. & Yanagisawa, T. 2006 Cell pattern of thermal convection induced by internal heating. Phys. Fluids 18, 038101.CrossRefGoogle Scholar
Jaupart, C., Labrosse, S., Lucazeau, F. & Mareschal, J. C. 2015 Temperatures, heat and energy in the mantle of the Earth. In Treatise on Geophysics, vol. 7, pp. 223–270. Elsevier.Google Scholar
Jellinek, A. M. & Jackson, M. G. 2015 Connections between the bulk composition, geodynamics and habitability of Earth. Nat. Geosci. 8, 587–593.Google Scholar
Kaminski, E. & Jaupart, C. 2003 Laminar starting plumes in high-Prandtl-number fluids. J. Fluid Mech. 478, 287–298.Google Scholar
Kulacki, F. A. & Emara, A. A. 1977 Steady and transient thermal convection in a fluid layer with uniform volumetric energy sources. J. Fluid Mech. 83, 375–395.Google Scholar
Kulacki, F. A. & Goldstein, R. J. 1975 Hydrodynamic instability in fluid layers with uniform volumetric energy sources. Appl. Sci. Res. 31, 81–109.Google Scholar
Kulacki, F. A. & Nagle, M. E. 1975 Natural convection in a horizontal fluid layer with volumetric energy sources. Trans. ASME J. Heat Transfer 97, 204–211.Google Scholar
Labrosse, S. 2002 Hotspots, mantle plumes and core heat loss. Earth Planet. Sci. Lett. 199, 147–156.Google Scholar
Labrosse, S., Poirier, J. P. & Le Mouël, J. L. 2001 The age of the inner core. Earth Planet. Sci. Lett. 190, 111–123.Google Scholar
Lay, T., Hernlund, J., Garnero, E. J. & Thorne, M. S. 2006 A post-Perovskite lens and D ′′ heat flux beneath the central Pacific. Science 314 (5803), 1272–1276.Google Scholar
Limare, A., Vilella, K., Di Giuseppe, E., Farnetani, C., Kaminski, E., Surducan, E., Surducan, V., Neamtu, C., Fourel, L. & Jaupart, C. 2015 Microwave-heating laboratory experiments for planetary mantle convection. J. Fluid Mech. 1565, 14–18.Google Scholar
McKenzie, D. P., Roberts, J. M. & Weiss, N. O. 1973 Numerical models of convection in the Earth’s mantle. Tectonophysics 19, 89–103.Google Scholar
Mitrovica, J. X. & Forte, A. M. 2004 A new inference of mantle viscosity based upon joint inversion of convection and glacial isostatic adjustment data. Earth Planet. Sci. Lett. 225, 177–189.Google Scholar
Moore, W. B. 2008 Heat transport in a convecting layer heated from within and below. J. Geophys. Res. 113, B11407.Google Scholar
Mora, G., Seton, M., Quevedo, L. & Müller, R. D. 2013 Organization of the tectonic plates in the last 200 Myr. Earth Planet. Sci. Lett. 373, 93–101.CrossRefGoogle Scholar
Nakagawa, T. & Tackley, P. J. 2014 Influence of combined primordial layering and recycled MORB on the coupled thermal evolution of Earth’s mantle and core. Geochem. Geophys. Geosyst. 15, 619–633.Google Scholar
Parmentier, E. M. & Sotin, C. 2000 Three-dimensional numerical experiments on thermal convection in a very viscous fluid: implications for the dynamics of a thermal boundary layer at high Rayleigh number. Phys. Fluids 12, 609–617.Google Scholar
Ritsema, J., Deuss, A., Van Heijst, H. J. & Woodhouse, J. H. 2011 S40rts: a degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys. J. Intl 184 (3), 1223–1236.CrossRefGoogle Scholar
Roberts, P. H. 1967 Convection in horizontal layers with internal heat generation: theory. J. Fluid Mech. 30, 33–49.Google Scholar
Rolf, T., Coltice, N. & Tackley, P. J. 2012 Linking continental drift, plate tectonics and the thermal state of the Earth’s mantle. Earth Planet. Sci. Lett. 351, 134–146.Google Scholar
Samuel, H. & Farnetani, C. G. 2003 Thermochemical convection and helium concentrations in mantle plumes. Earth Planet. Sci. Lett. 207, 39–56.Google Scholar
Schubert, G., Hussmann, H., Lainey, V., Matson, D. L., McKinnon, W. B., Sohl, F., Sotin, C., Tobie, G., Turrini, D. & Van Hoolst, T. 2010 Evolution of icy satellites. Space Sci. Rev. 153, 447–484.Google Scholar
Schubert, G., Turcotte, D. L. & Olson, P. 2001 Mantle Convection in the Earth and Planets. Cambridge University Press.Google Scholar
Seis, C. 2013 Laminar boundary layers in convective heat transport. Commun. Math. Phys. 324, 995–1031.Google Scholar
Shirey, S. B. & Richardson, S. H. 2011 Start of the Wilson cycle at 3 Ga shown by diamonds from the subcontinental mantle. Science 333, 434–436.Google Scholar
Shishkina, O. & Wagner, C. 2008 Analysis of sheet-like thermal plumes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 599, 383–404.Google Scholar
Smrekar, S. E. & Sotin, C. 2012 Constraints on mantle plumes on Venus: implications for volatile history. Icarus 217, 510–523.Google Scholar
Stixrude, L. & Lithgow-Bertelloni, C. 2011 Thermodynamics of mantle minerals? Part II. Phase equilibria. Geophys. J. Intl 184, 1180–1213.Google Scholar
Tackley, P. J. 1998a Self-consistent generation of tectonic plates in three-dimensional mantle convection. Earth Planet. Sci. Lett. 157, 9–22.Google Scholar
Tackley, P. J. 1998b Three-dimensional simulations of mantle convection with a thermochemical CMB boundary layer: D ′′ ? In The Core–Mantle Boundary Region (ed. Gurnis, M., Wysession, M. E., Knittle, E. & Buffett, B. A.), pp. 231–253. AGU.Google Scholar
Tackley, P. J. 2008 Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the yin-yang grid. Phys. Earth Planet. Inter. 171, 7–18.Google Scholar
Takahashi, J., Tasaka, Y., Murai, Y., Takeda, Y. & Yanagisawa, T. 2010 Experimental study of cell pattern formation induced by internal heat sources in a horizontal fluid layer. Intl J. Heat Mass Transfer 53, 1483–1490.Google Scholar
Theerthan, S. A. & Arakeri, J. H. 1994 Planform structure of turbulent Rayleigh–Bénard convection. Intl Commun. Heat Mass Transfer 21 (4), 561–572.Google Scholar
Tritton, D. J. & Zarraga, M. N. 1967 Convection in horizontal layers with internal heat generation. Experiments. J. Fluid Mech. 30, 21–31.Google Scholar
Turcotte, D. L. & Oxburgh, E. R. 1967 Finite amplitude convective cells and continental drift. J. Fluid Mech. 28 (1), 29–42.Google Scholar
Vilella, K. & Kaminski, E. 2017 Fully determined scaling laws for volumetrically heated convective systems, a tool for assessing habitability of exoplanets. Phys. Earth Planet. Inter. 266, 18–28.Google Scholar
Yujiro, O., Tetsuzo, S., Hinako, A., Hidekazu, T., Kantaro, F. & Hidetsugu, T. 1989 Structure and development of the Sagami trough and the Boso triple junction. Tectonophysics 160, 135–150.Google Scholar
Zhong, S. 2005 Dynamics of thermal plumes in three-dimensional isoviscous thermal convection. Geophys. J. Intl 162, 289–300.Google Scholar
Zhou, Q. & Xia, K. Q. 2010 Physical and geometrical properties of thermal plumes in turbulent Rayleigh–Bénard convection. New J. Phys. 12 (7), 075006.Google Scholar
Supplementary material: File

Vilella et al. supplementary material 1

Vilella et al. supplementary material

Download Vilella et al. supplementary material 1(File)
File 57.3 KB