Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T17:53:07.225Z Has data issue: false hasContentIssue false
  • English
  • Français

Fully nonlinear long-wave models in the presence of vorticity

Published online by Cambridge University Press:  27 October 2014

Angel Castro  and
David Lannes
Angel Castro
Affiliation:
Departamento de Matemáticas UAM, Instituto de Ciencias Matemáticas CSIC, Campus de Cantoblanco, 28049 Madrid, Spain
David Lannes*
Affiliation:
IMB, Institut Mathématique de Bordeaux et CNRS UMR 5251, 351 Cours de Libération, 33405 Talence CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

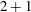We study here Green–Naghdi type equations (also called fully nonlinear Boussinesq, or Serre equations) modelling the propagation of large-amplitude waves in shallow water without a smallness assumption on the amplitude of the waves. The novelty here is that we allow for a general vorticity, thereby allowing complex interactions between surface waves and currents. We show that the a priori ($2+1$)-dimensional dynamics of the vorticity can be reduced to a finite cascade of two-dimensional equations. With a mechanism reminiscent of turbulence theory, vorticity effects contribute to the averaged momentum equation through a Reynolds-like tensor that can be determined by a cascade of equations. Closure is obtained at the precision of the model at the second order of this cascade. We also show how to reconstruct the velocity field in the (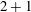$2+1$)-dimensional fluid domain from this set of two-dimensional equations and exhibit transfer mechanisms between the horizontal and vertical components of the vorticity, thus opening perspectives for the study of rip currents, for instance.

JFM classification

Geophysical and Geological Flows: Shallow water flows Waves/Free-surface Flows: Shear waves Waves/Free-surface Flows: Surface gravity waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 642 - 675
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvarez-Samaniego, B. & Lannes, D. 2008 Large time existence for 3D water-waves and asymptotics. Invent. Math. 171, 485–541.CrossRefGoogle Scholar
Bonneton, P., Barthelemy, E., Chazel, F., Cienfuegos, R., Lannes, D., Marche, F. & Tissier, M. 2011a Recent advances in Serre–Green–Naghdi modelling for wave transformation, breaking and runup processes. Eur. J. Mech. (B/Fluids) 30, 589–597.CrossRefGoogle Scholar
Bonneton, P., Chazel, F., Lannes, D., Marche, F. & Tissier, M. 2011b A splitting approach for the fully nonlinear and weakly dispersive Green–Naghdi model. J. Comput. Phys. 230, 1479–1498.CrossRefGoogle Scholar
Bowen, A. J. 1969 The generation of longshore currents on a plane beach. J. Mar. Res. 27, 206–215.Google Scholar
Castro, A. & Lannes, D.Well-posedness and shallow-water stability for a new Hamiltonian formulation of the water waves equations with vorticity (submitted).Google Scholar
Chen, Q., Dalrymple, R. A. & Kirby, J. T. 1999 Boussinesq modeling of a rip current system. J. Geophys. Res. 104, 617–637.Google Scholar
Chen, Q., Kirby, J. T., Dalrymple, R. A., Kennedy, A. B. & Chawla, A. 2000 Boussinesq modeling of wave transformation, breaking, and runup. II: 2D. J. Waterways Port Coast. Ocean Engng 126, 48–56.CrossRefGoogle Scholar
Chen, Q., Kirby, J. T., Dalrymple, R. A., Shi, F. & Thornton, E. B. 2003 Boussinesq modeling of longshore currents. J. Geophys. Res. 108 (C11), 3362.Google Scholar
Cienfuegos, R., Bartélemy, E. & Bonneton, P. 2006 A fourth-order compact finite volume scheme for fully nonlinear and weakly dispersive Boussinesq-type equations. Part I: model development and analysis. Intl J. Numer. Meth. Fluids 56, 1217–1253.CrossRefGoogle Scholar
Constantin, A. 2001 Nonlinear Water Waves with Applications to Wave–Current Interactions and Tsunamis, CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 81. SIAM.Google Scholar
Constantin, A. & Varvaruca, E. 2011 Steady periodic water waves with constant vorticity: regularity and local bifurcation. Arch. Rat. Mech. Anal. 199, 33–67.CrossRefGoogle Scholar
Dutykh, D., Clamond, D., Milewski, P. & Mitsotakis, D. 2013 Finite volume and pseudo-spectral schemes for the fully nonlinear 1D Serre equations. Eur. J. Appl. Maths 24 (5), 761–787.CrossRefGoogle Scholar
Gavrilyuk, S. & Gouin, H. 2012 Geometric evolution of the Reynolds stress tensor. Intl J. Engng Sci. 59, 65–73.CrossRefGoogle Scholar
Hammack, J., Scheffner, N. & Segur, H. 1991 A note on the generation and narrowness of periodic rip currents. J. Geophys. Res. Oceans 96, 4909–4914.CrossRefGoogle Scholar
Iguchi, T. 2009 A shallow water approximation for water waves. J. Math. Kyoto Univ. 49, 13–55.Google Scholar
Kano, T. & Nishida, T. 1979 Sur les ondes de surface de l’eau avec une justification mathématique des équations des ondes en eau peu profonde. J. Math. Kyoto Univ. 19, 335–370.Google Scholar
Kazolea, M., Delis, A. I., Nikolos, I. K. & Synolakis, C. E. 2012 An unstructured finite volume numerical scheme for extended 2D Boussinesq-type equations. Coast. Engng 69, 42–66.CrossRefGoogle Scholar
Kim, J. W., Bai, K. J., Ertekin, R. C. & Webster, W. C. 2001 A derivation of the Green–Naghdi equations for irrotational flows. J. Engng Math. 40, 17–42.CrossRefGoogle Scholar
Kim, D.-H., Lynett, P. J. & Socolofsky, S. A. 2009 A depth-integrated model for weakly dispersive, turbulent, and rotational fluid flows. Ocean Model. 27, 198–214.CrossRefGoogle Scholar
Lannes, D. 2013 The Water Waves Problem: Mathematical Analysis and Asymptotics, Mathematical Surveys and Monographs, vol. 188. American Mathematical Society.Google Scholar
Lannes, D. & Bonneton, P. 2009 Derivation of asymptotic two-dimensional time-dependent equations for surface water wave propagation. Phys. Fluids 21, 016601.CrossRefGoogle Scholar
Lannes, D. & Marche, F.A new class of fully nonlinear and weakly dispersive Green–Naghdi models for efficient 2D simulations (submitted).Google Scholar
Le Métayer, O., Gavrilyuk, S. & Hank, S. 2010 A numerical scheme for the Green–Naghdi model. J. Comput. Phys. 229, 2034–2045.CrossRefGoogle Scholar
Li, Y. A. 2006 A shallow-water approximation to the full water wave problem. Commun. Pure Appl. Maths 59, 1225–1285.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1970 Longshore currents generated by obliquely incident sea waves. J. Geophys. Res. 75, 6778–6789.CrossRefGoogle Scholar
Makarenko, N. 1986 A second long-wave approximation in the Cauchy–Poisson problem. Dyn. Contin. Media 77, 56–72.Google Scholar
Mohammadi, B. & Pironneau, O. 1994 Analysis of the K-Epsilon Turbulence Model, Research in Applied Mathematics. John Wiley & Sons.Google Scholar
Musumeci, R. E., Svendsen, I. A. & Veeramony, J. 2005 The flow in the surf zone: a fully nonlinear Boussinesq-type of approach. Coast. Engng 52, 565–598.CrossRefGoogle Scholar
Ovsjannikov, L. V. 1976 Cauchy problem in a scale of Banach spaces and its application to the shallow water theory justification. In Appl. Meth. Funct. Anal. Probl. Mech. (IUTAM/IMU-Symp., Marseille, 1975), Lecture Notes in Mathematics, vol. 503, pp. 426–437.Google Scholar
Pope, S. B. 2005 Turbulent Flows. Cambridge University Press.Google Scholar
Ricchiuto, M. & Filippini, A. G. 2014 Upwind residual discretization of enhanced Boussinesq equations for wave propagation over complex bathymetries. J. Comput. Phys. 271, 306–341.CrossRefGoogle Scholar
Richard, G. L. & Gavrilyuk, S. L. 2012 A new model of roll waves: comparison with Brock’s experiments. J. Fluid Mech. 698, 374–405.CrossRefGoogle Scholar
Richard, G. L. & Gavrilyuk, S. L. 2013 The classical hydraulic jump in a model of shear shallow-water flows. J. Fluid Mech. 725, 492–521.CrossRefGoogle Scholar
Shields, J. J. & Webster, W. C. 1988 On direct methods in water-wave theory. J. Fluid Mech. 197, 171–199.CrossRefGoogle Scholar
Svendsen, I. A. & Putrevu, U. 1995 Surf-zone hydrodynamics. Adv. Coast. Ocean Engng 2, 1–78.Google Scholar
Teshukov, V. M. 2007 Gas-dynamic analogy in the theory of stratified liquid flows with a free boundary. Izv. Ross. Akad. Nauk Mekh. Zhidk. Gaza 5, 143–153.Google Scholar
Veeramony, J. & Svendsen, I. A. 2000 The flow in surf-zone waves. Coast. Engng 39, 93–122.CrossRefGoogle Scholar
Wahlen, E. 2009 Steady water waves with a critical layer. J. Differ. Equ. 246, 2468–2483.CrossRefGoogle Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194.CrossRefGoogle Scholar
Zhang, Y., Kennedy, A. B., Panda, N., Dawson, C. & Westerink, J. J. 2013 Boussinesq–Green–Naghdi rotational water wave theory. Coast. Engng 73, 13–27.CrossRefGoogle Scholar