Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dauhajre, Daniel P.
and
McWilliams, James C.
2018.
Diurnal Evolution of Submesoscale Front and Filament Circulations.
Journal of Physical Oceanography,
Vol. 48,
Issue. 10,
p.
2343.
Crowe, Matthew N.
and
Taylor, John R.
2018.
The evolution of a front in turbulent thermal wind balance. Part 1. Theory.
Journal of Fluid Mechanics,
Vol. 850,
Issue. ,
p.
179.
Wenegrat, Jacob O.
Thomas, Leif N.
Gula, Jonathan
and
McWilliams, James C.
2018.
Effects of the Submesoscale on the Potential Vorticity Budget of Ocean Mode Waters.
Journal of Physical Oceanography,
Vol. 48,
Issue. 9,
p.
2141.
Pham, Hieu T.
and
Sarkar, Sutanu
2018.
Ageostrophic Secondary Circulation at a Submesoscale Front and the Formation of Gravity Currents.
Journal of Physical Oceanography,
Vol. 48,
Issue. 10,
p.
2507.
Liang, Jun-Hong
Wan, Xiaoliang
Rose, Kenneth A.
Sullivan, Peter P.
and
McWilliams, James C.
2018.
Horizontal Dispersion of Buoyant Materials in the Ocean Surface Boundary Layer.
Journal of Physical Oceanography,
Vol. 48,
Issue. 9,
p.
2103.
Large, William G.
Patton, Edward G.
DuVivier, Alice K.
Sullivan, Peter P.
and
Romero, Leonel
2019.
Similarity Theory in the Surface Layer of Large-Eddy Simulations of the Wind-, Wave-, and Buoyancy-Forced Southern Ocean.
Journal of Physical Oceanography,
Vol. 49,
Issue. 8,
p.
2165.
Crowe, Matthew N.
and
Taylor, John R.
2019.
The evolution of a front in turbulent thermal wind balance. Part 2. Numerical simulations.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
326.
Verma, Vicky
Pham, Hieu T.
and
Sarkar, Sutanu
2019.
The submesoscale, the finescale and their interaction at a mixed layer front.
Ocean Modelling,
Vol. 140,
Issue. ,
p.
101400.
Chamecki, Marcelo
Chor, Tomas
Yang, Di
and
Meneveau, Charles
2019.
Material Transport in the Ocean Mixed Layer: Recent Developments Enabled by Large Eddy Simulations.
Reviews of Geophysics,
Vol. 57,
Issue. 4,
p.
1338.
Pearson, Brodie C.
Grant, Alan L. M.
and
Polton, Jeff A.
2019.
Pressure–strain terms in Langmuir turbulence.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
5.
Shao, Mingming
Ortiz‐Suslow, David G.
Haus, Brian K.
Lund, Björn
Williams, Neil J.
Özgökmen, Tamay M.
Laxague, Nathan J. M.
Horstmann, Jochen
and
Klymak, Jody M.
2019.
The Variability of Winds and Fluxes Observed Near Submesoscale Fronts.
Journal of Geophysical Research: Oceans,
Vol. 124,
Issue. 11,
p.
7756.
Bodner, Abigail S.
Fox-Kemper, Baylor
Van Roekel, Luke P.
McWilliams, James C.
and
Sullivan, Peter P.
2019.
A perturbation approach to understanding the effects of turbulence on frontogenesis.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Sullivan, Peter P.
and
McWilliams, James C.
2019.
Langmuir turbulence and filament frontogenesis in the oceanic surface boundary layer.
Journal of Fluid Mechanics,
Vol. 879,
Issue. ,
p.
512.
McWilliams, James C.
2019.
A survey of submesoscale currents.
Geoscience Letters,
Vol. 6,
Issue. 1,
Pham, Hieu T.
and
Sarkar, Sutanu
2019.
The role of turbulence in strong submesoscale fronts of the Bay of Bengal.
Deep Sea Research Part II: Topical Studies in Oceanography,
Vol. 168,
Issue. ,
p.
104644.
Smith, Travis A.
Jolliff, Jason K.
Walker, Nan D.
and
Anderson, Stephanie
2019.
Biophysical Submesoscale Processes in the Wake of Hurricane Ivan: Simulations and Satellite Observations.
Journal of Marine Science and Engineering,
Vol. 7,
Issue. 11,
p.
378.
Barkan, Roy
Molemaker, M. Jeroen
Srinivasan, Kaushik
McWilliams, James C.
and
D’Asaro, Eric A.
2019.
The Role of Horizontal Divergence in Submesoscale Frontogenesis.
Journal of Physical Oceanography,
Vol. 49,
Issue. 6,
p.
1593.
Romero, Leonel
Ohlmann, J. Carter
Pallàs-Sanz, Enric
Statom, Nicholas M.
Pérez-Brunius, Paula
and
Maritorena, Stéphane
2019.
Coincident Observations of Dye and Drifter Relative Dispersion over the Inner Shelf.
Journal of Physical Oceanography,
Vol. 49,
Issue. 9,
p.
2447.
Villas Bôas, Ana B.
Ardhuin, Fabrice
Ayet, Alex
Bourassa, Mark A.
Brandt, Peter
Chapron, Betrand
Cornuelle, Bruce D.
Farrar, J. T.
Fewings, Melanie R.
Fox-Kemper, Baylor
Gille, Sarah T.
Gommenginger, Christine
Heimbach, Patrick
Hell, Momme C.
Li, Qing
Mazloff, Matthew R.
Merrifield, Sophia T.
Mouche, Alexis
Rio, Marie H.
Rodriguez, Ernesto
Shutler, Jamie D.
Subramanian, Aneesh C.
Terrill, Eric J.
Tsamados, Michel
Ubelmann, Clement
and
van Sebille, Erik
2019.
Integrated Observations of Global Surface Winds, Currents, and Waves: Requirements and Challenges for the Next Decade.
Frontiers in Marine Science,
Vol. 6,
Issue. ,
Grisouard, Nicolas
and
Zemskova, Varvara E.
2020.
Ekman-inertial instability.
Physical Review Fluids,
Vol. 5,
Issue. 12,
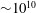 ${\sim}10^{10}$ grid points. Steady winds are oriented in directions perpendicular or parallel to the filament axis. Due to turbulent vertical momentum mixing, cold filaments generate a potent two-celled secondary circulation in the cross-filament plane that is frontogenetic, sharpens the cross-filament buoyancy and horizontal velocity gradients and blocks Ekman buoyancy flux across the cold filament core towards the warm filament edge. Within less than a day, the frontogenesis is arrested at a small width,
${\sim}10^{10}$ grid points. Steady winds are oriented in directions perpendicular or parallel to the filament axis. Due to turbulent vertical momentum mixing, cold filaments generate a potent two-celled secondary circulation in the cross-filament plane that is frontogenetic, sharpens the cross-filament buoyancy and horizontal velocity gradients and blocks Ekman buoyancy flux across the cold filament core towards the warm filament edge. Within less than a day, the frontogenesis is arrested at a small width, 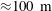 ${\approx}100~\text{m}$, primarily by an enhancement of the turbulence through a small submesoscale, horizontal shear instability of the sharpened filament, followed by a subsequent slow decay of the filament by further turbulent mixing. The boundary-layer turbulence is inhomogeneous and non-stationary in relation to the evolving submesoscale currents and density stratification. The occurrence of frontogenesis and arrest are qualitatively similar with varying stress direction or with convective cooling, but the detailed evolution and flow structure differ among the cases. Thus submesoscale filament frontogenesis caused by boundary-layer turbulence, frontal arrest by frontal instability and frontal decay by forward energy cascade, and turbulent mixing are generic processes in the upper ocean.
${\approx}100~\text{m}$, primarily by an enhancement of the turbulence through a small submesoscale, horizontal shear instability of the sharpened filament, followed by a subsequent slow decay of the filament by further turbulent mixing. The boundary-layer turbulence is inhomogeneous and non-stationary in relation to the evolving submesoscale currents and density stratification. The occurrence of frontogenesis and arrest are qualitatively similar with varying stress direction or with convective cooling, but the detailed evolution and flow structure differ among the cases. Thus submesoscale filament frontogenesis caused by boundary-layer turbulence, frontal arrest by frontal instability and frontal decay by forward energy cascade, and turbulent mixing are generic processes in the upper ocean.