Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T08:35:12.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Front dynamics and entrainment of finite circular gravity currents on an unbounded uniform slope

Published online by Cambridge University Press:  21 July 2016

N. Zgheib ,
A. Ooi  and
S. Balachandar
N. Zgheib
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); UMR 5502, Allée Camille Soula, F-31400 Toulouse, France
A. Ooi
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Parkville 3010, Australia
S. Balachandar*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report on the dynamics of circular finite-release Boussinesq gravity currents on a uniform slope. The study comprises a series of highly resolved direct numerical simulations for a range of slope angles between 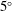$5^{\circ }$ and 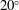$20^{\circ }$. The simulations were fixed at Reynolds number 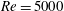$Re=5000$ for all slopes considered. The temporal evolution of the front is compared to available experimental data. One of the interesting aspects of this study is the detection of a converging flow towards the centre of the gravity current. This converging flow is a result of the finite volume of the release coupled with the presence of a sloping boundary, which results in a second acceleration phase in the front velocity of the current. The details of the dynamics of this second acceleration and the redistribution of material in the current leading to its development will be discussed. These finite-release currents are invariably dominated by the head where most of the mixing and ambient entrainment occurs. We propose a simple method for defining the head of the current from which we extract various properties including the front Froude number and entrainment coefficient. The Froude number is seen to increase with steeper slopes, whereas the entrainment coefficient is observed to be weakly dependent on the bottom slope.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 322 - 352
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anjum, H. J., Mcelwaine, J. N. & Caulfield, C. C. P. 2013 The instantaneous Froude number and depth of unsteady gravity currents. J. Hydraul. Res. 51 (1), 432–445.Google Scholar
Beghin, P., Hopfinger, E. J. & Britter, R. E. 1981 Gravitational convection from instantaneous sources on inclined boundaries. J. Fluid Mech. 107, 407–422.Google Scholar
Birman, V., Martin, J. E. & Meiburg, E. 2005 The non-Boussinesq lock-exchange problem. Part 2. High-resolution simulations. J. Fluid Mech. 537, 125–144.Google Scholar
Blanchette, F., Strauss, M., Meiburg, E., Kneller, B. & Glinsky, M. 2005 High-resolution numerical simulations of resuspending gravity currents: condition for self-sustainment. J. Geophys. Res. 110, c12022.Google Scholar
Bonometti, T. & Balachandar, S. Effect of Schmidt number on the structure and propagation of density currents. Theor. Comput. Fluid Dyn. 22, 341–361.Google Scholar
Britter, R. E. & Linden, P. F. 1980 The motion of the front of a gravity current travelling down an incline. J. Fluid Mech. 99, 531–543.Google Scholar
Cantero, M., Balachandar, S. & Garcia, M. 2007a High-resolution simulations of cylindrical density currents. J. Fluid Mech. 590, 437–469.CrossRefGoogle Scholar
Cantero, M., Balachandar, S., García, M. & Ferry, J. P. 2006 Direct numerical simulations of planar and cylindrical density currents. Trans. ASME E: J. Appl. Mech. 73, 923–930.CrossRefGoogle Scholar
Cantero, M., Lee, J. R., Balachandar, S. & Garcia, M. 2007b On the front velocity of gravity currents. J. Fluid Mech. 586, 1–39.Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Cortese, T. & Balachandar, S. 1995 High performance spectral simulation of turbulent flows in massively parallel machines with distributed memory. Intl J. Supercomputer Appl. 9, 187–204.Google Scholar
Dai, A. 2013 Experiments on gravity currents propagating on different bottom slopes. J. Fluid Mech. 731, 117–141.Google Scholar
Dai, A., Ozdemir, C. E., Cantero, M. I. & Balachandar, S. 2012 Gravity currents from instantaneous sources down a slope. J. Hydraul. Engng ASCE 138, 237–246.Google Scholar
Fleischmann, C. M. & McGrattan, K. B. 1999 Numerical and experimental gravity currents related to backdrafts. Fire Safety J. 33, 21–34.Google Scholar
Härtel, C., Fredrik, C. & Mattias, T. 2000 Analysis and direct numerical simulation of the flow at a gravity-current head. Part 2. The lobe-and-cleft instability. J. Fluid Mech. 418, 213–229.Google Scholar
Huppert, H. E. & Simpson, J. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.Google Scholar
Marino, B. M., Thomas, L. P. & Linden, P. F. 2005 The front condition for gravity currents. J. Fluid Mech. 536, 49–78.Google Scholar
Maxworthy, T. 2010 Experiments on gravity currents propagating down slopes. Part 2. The evolution of a fixed volume of fluid released from closed locks into a long, open channel. J. Fluid Mech. 647, 27–51.Google Scholar
Ottolenghi, L., Adduce, C., Inghilesi, R., Roman, F. & Armenio, V. 2015 Large eddy simulation of gravity currents moving on up-sloping boundaries. In Informatics, Networking and Intelligent Computing: Proceedings of the 2014 International Conference on Informatics, Networking and Intelligent Computing (INIC 2014), 16–17 November 2014, Shenzhen, China, p. 189. CRC Press.Google Scholar
Ross, A. N., Linden, P. F. & Dalziel, S. B. 2002 A study of three-dimensional gravity currents on a uniform slope. J. Fluid Mech. 453, 239–261.Google Scholar
Simpson, J. E. 1972 Effects of the lower boundary on the head of a gravity current. J. Fluid Mech. 53, 759–768.Google Scholar
Simpson, J. E. 1982 Gravity currents in the laboratory, atmosphere and oceans. Annu. Rev. Fluid Mech. 14, 213–234.Google Scholar
Tickle, G. A. 1996 A model of the motion and dilution of a heavy gas cloud released on a uniform slope in calm conditions. J. Hazard. Mater. 49, 29–47.Google Scholar
Turnbull, B. & McElwaine, J. N. 2007 A comparison of powder-snow avalanches at Vallee de la Sionne, Switzerland, with plume theories. J. Glaciol. 53, 30–40.CrossRefGoogle Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Webber, D. M., Jones, S. J. & Martin, D. 1993 A model of the motion of a heavy gas cloud released on a uniform slope. J. Hazard. Mater. 33, 101–122.Google Scholar
Zgheib, N., Bonometti, T. & Balachandar, S. 2015 Propagation and deposition of non-circular finite release particle-laden currents. Phys. Fluids 27 (5), 086604.Google Scholar
Zhou, J., Adrian, R., Balachandar, S. & Kendall, T. 1999 Mechanics for generating coherent packets of hairpin vortices. J. Fluid Mech. 387, 353–396.Google Scholar