Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-09T22:12:01.080Z Has data issue: false hasContentIssue false
  • English
  • Français

From travelling waves to mild chaos: a supercritical bifurcation cascade in pipe flow

Published online by Cambridge University Press:  29 August 2012

F. Mellibovsky  and
B. Eckhardt
F. Mellibovsky*
Affiliation:
Departament de Física Aplicada, Universitat Politècnica de Catalunya, 08034, Barcelona, Spain
B. Eckhardt
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, D-35032 Marburg, Germany J.M. Burgerscentrum, Delft University of Technology, 2638 CD Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study numerically a succession of transitions in pipe Poiseuille flow that lead from simple travelling waves to waves with chaotic time-dependence. The waves at the origin of the bifurcation cascade are twofold azimuthally periodic, shift–reflect symmetric, and have a non-dimensional axial wavelength of 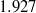diameters. As the Reynolds number is increased, successive transitions result in a wide range of time-dependent solutions that include spiralling, modulated travelling, modulated spiralling, doubly modulated spiralling and mildly chaotic waves. Numerical evidence suggests that the latter spring from heteroclinic tangles of the stable and unstable invariant manifolds of two shift–reflect symmetric, modulated travelling waves. The chaotic set thus produced is confined to a limited range of Reynolds numbers, bounded by the occurrence of manifold tangencies. The subspace of discrete symmetry to which the states studied here belong makes many of the bifurcation and path-following investigations presented readily accessible. However, we expect that most of the phenomenology carries over to the full state space, thus suggesting a mechanism for the formation and break-up of invariant states that can give rise to chaotic dynamics.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Chaos Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 709 , 25 October 2012 , pp. 149 - 190
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Anischenko, V. S., Safonova, M. A. & Chua, L. O. 1993 Confirmation of the Afraimovich–Shilnikov torus-breakdown theorem via a torus circuit. IEEE Trans. Cir. Sys. 40 (11), 792–800.Google Scholar
2. Avila, K., Moxey, D., de Lozar, A., Avila, M. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.CrossRefGoogle ScholarPubMed
3. Avila, M., Willis, A. P. & Hof, B. 2010 On the transient nature of localized pipe flow turbulence. J. Fluid Mech. 646, 127–136.CrossRefGoogle Scholar
4. Boberg, L. & Brosa, U. 1988 Onset of turbulence in a pipe. Z. Naturforsch. A 43, 697–726.CrossRefGoogle Scholar
5. Brosa, U. & Grossmann, S. 1999 Minimum description of the onset of pipe turbulence. Eur. Phys. J. B 9 (2), 343–354.CrossRefGoogle Scholar
6. Chenciner, A. & Iooss, G. 1979 Bifurcation of invariant torus. Arch. Rat. Mech. Anal. 69 (2), 109–198.CrossRefGoogle Scholar
7. Chossat, P. & Lauterbach, R. 2000 Methods in Equivariant Bifurcations and Dynamical Systems. World Scientific.Google Scholar
8. Crawford, J. D. & Knobloch, E. 1991 Symmetry and symmetry-breaking bifurcations in fluid dynamics. Annu. Rev. Fluid Mech. 23, 341–387.CrossRefGoogle Scholar
9. Darbyshire, A. G. & Mullin, T. 1995 Transition to turbulence in constant-mass-flux pipe flow. J. Fluid Mech. 289, 83–114.CrossRefGoogle Scholar
10. Duguet, Y., Pringle, C. C. T. & Kerswell, R. R. 2008 Relative periodic orbits in transitional pipe flow. Phys. Fluids 20 (11), 114102.CrossRefGoogle Scholar
11. Duguet, Y., Willis, A. P. & Kerswell, R. R. 2008 Transition in pipe flow: the saddle structure on the boundary of turbulence. J. Fluid Mech. 613, 255–274.CrossRefGoogle Scholar
12. Eckhardt, B. 2009 Introduction. Turbulence transition in pipe flow: 125th anniversary of the publication of Reynolds’ paper. Phil. Trans. R. Soc. Lond. A 367 (1888), 449–455.Google ScholarPubMed
13. Eckhardt, B., Faisst, H., Schmiegel, A. & Schneider, T. M. 2008 Dynamical systems and the transition to turbulence in linearly stable shear flows. Phil. Trans. R. Soc. Lond. A 366, 1297–1315.Google ScholarPubMed
14. Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.CrossRefGoogle Scholar
15. Ehrenstein, U. & Koch, W. 1991 Three-dimensional wave-like equilibrium states in plane Poiseuille flow. J. Fluid Mech. 228, 111–148.Google Scholar
16. Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91 (22), 224502.CrossRefGoogle ScholarPubMed
17. Gaspard, P. 1990 Measurement of the instability rate of a far-from-equilibrium steady state at an infinite period bifurcation. J. Phys. Chem. 94 (1), 1–3.Google Scholar
18. Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.CrossRefGoogle Scholar
19. Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
20. Golubitsky, M., LeBlanc, V. G. & Melbourne, I. 2000 Hopf bifurcation from rotating waves and patterns in physical space. J. Nonlinear Sci. 10 (1), 69–101.CrossRefGoogle Scholar
21. Golubitsky, M., Stewart, I. & Schaeffer, D. G. 1988 Singularities and groups in bifurcation theory, vol. 2. In Applied Mathematical Sciences, vol. 69. Springer.Google Scholar
22. Grossmann, S. 2000 The onset of shear flow turbulence. Rev. Mod. Phys. 72 (2), 603–618.CrossRefGoogle Scholar
23. Hof, B., van Doorne, C. W. H., Westerweel, J., Nieuwstadt, F. T. M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear travelling waves in turbulent pipe flow. Science 305 (5690), 1594–1598.Google Scholar
24. Hof, B., Schneider, T. M., Westerweel, J. & Eckhardt, B. 2006 Finite lifetime of turbulence in shear flows. Nature 443 (7107), 59–62.Google Scholar
25. Kerswell, R. R. & Tutty, O. R. 2007 Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
26. Krupa, M. 1990 Bifurcations of relative equilibria. SIAM J. Math. Anal. 21 (6), 1453–1486.CrossRefGoogle Scholar
27. Kuznetsov, Y. A. 1995 Elements of Applied Bifurcation Theory, third edition. Springer.Google Scholar
28. Kuznetsov, Y. A., Meijer, H. G. E. & Van Veen, L. 2004 The fold-flip bifurcation. Intl J. Bifurcation Chaos 14 (7), 2253–2282.CrossRefGoogle Scholar
29. Landau, L. 1944 On the problem of turbulence. Dokl. Akad. Nauk SSSR 44, 339–342.Google Scholar
30. Marques, F., Lopez, J. M. & Shen, J. 2001 A periodically forced flow displaying symmetry breaking via a three-tori gluing bifurcation and two-tori resonances. Physica D 156, 81–97.CrossRefGoogle Scholar
31. Meca, E., Mercader, I., Batiste, O. & Ramírez-Piscina, L. 2004 Blue sky catastrophe in double-diffusive convection. Phys. Rev. Lett. 92 (23), 234501.CrossRefGoogle Scholar
32. Mellibovsky, F. & Eckhardt, B. 2011 Takens–Bogdanov bifurcation of travelling wave solutions in pipe flow. J. Fluid Mech. 670, 96–129.Google Scholar
33. Mellibovsky, F. & Meseguer, A. 2009 Critical threshold in pipe flow transition. Phil. Trans. R. Soc. Lond. A 367 (1888), 545–560.Google ScholarPubMed
34. Meseguer, A. & Mellibovsky, F. 2007 On a solenoidal Fourier–Chebyshev spectral method for stability analysis of the Hagen–Poiseuille flow. Appl. Numer. Math. 57, 920–938.CrossRefGoogle Scholar
35. Meseguer, A. & Trefethen, L. N. 2003 Linearized pipe flow to Reynolds number . J. Comput. Phys. 186, 178–197.CrossRefGoogle Scholar
36. Nagata, M. 1997 Three-dimensional travelling-wave solutions in plane Couette flow. Phys. Rev. E 55 (2), 2023–2025.CrossRefGoogle Scholar
37. Newhouse, S., Ruelle, D. & Takens, F. 1978 Occurrence of strange axiom attractors near quasi-periodic flows on . Commun. Math. Phys. 64, 35–40.CrossRefGoogle Scholar
38. Pfenniger, W. 1961 Boundary Layer and Flow Control. (ed. Lachman, G. V. ). pp. 970–980. Pergamon.Google Scholar
39. Pringle, C. C. T., Duguet, Y. & Kerswell, R. R. 2009 Highly symmetric travelling waves in pipe flow. Phil. Trans. R. Soc. Lond. A 367 (1888), 457–472.Google ScholarPubMed
40. Pringle, C. C. T. & Kerswell, R. R. 2007 Asymmetric, helical, and mirror-symmetric travelling waves in pipe flow. Phys. Rev. Lett. 99 (7), 074502.Google Scholar
41. Pugh, J. D. & Saffman, P. G. 1988 Two-dimensional superharmonic stability of finite-amplitude waves in plane Poiseuille flow. J. Fluid Mech. 194, 295–307.Google Scholar
42. Rand, D. 1982 Dynamics and symmetry: predictions for modulated waves in rotating fluids. Arch. Rat. Mech. Anal. 79 (1), 1–37.Google Scholar
43. Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous and of the law of resistance in parallel channels. Phil. Trans. R. Soc. Lond. 174, 935–982.Google Scholar
44. Ruelle, D. & Takens, F. 1971 On the nature of turbulence. Commun. Math. Phys. 20, 167–192.Google Scholar
45. Sanchez, J., Net, M. & Simo, C. 2010 Computation of invariant tori by Newton–Krylov methods in large-scale dissipative systems. Physica D 239, 123–133.CrossRefGoogle Scholar
46. Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, eighth edition. Springer.Google Scholar
47. Schmid, P. J. & Henningson, D. S. 1994 Optimal energy growth in Hagen–Poiseuille flow. J. Fluid Mech. 277, 197–225.CrossRefGoogle Scholar
48. Schneider, T. M. & Eckhardt, B. 2009 Edge states intermediate between laminar and turbulent dynamics in pipe flow. Phil. Trans. R. Soc. Lond. A 367 (1888), 577–587.Google Scholar
49. Schneider, T. M., Eckhardt, B. & Vollmer, J. 2007 Statistical analysis of coherent structures in transitional pipe flow. Phys. Rev. E 75 (6), 066313.Google Scholar
50. Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and edge of chaos in pipe flow. Phys. Rev. Lett. 99 (3), 034502.Google Scholar
51. Shan, H., Ma, B., Zhang, Z. & Nieuwstadt, F. T. M. 1999 On the spatial evolution of a wall-imposed periodic disturbance in pipe Poiseuille flow at . Part 1. Subcritical disturbance. J. Fluid Mech. 398, 181–224.Google Scholar
52. Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96 (17), 174101.Google Scholar
53. Soibelman, I. & Meiron, D. I. 1991 Finite-amplitude bifurcations in plane Poiseuille flow: two-dimensional Hopf bifurcation. J. Fluid Mech. 229, 389–416.CrossRefGoogle Scholar
54. Strogatz, S. H. 1994 Nonlinear Dynamics and Chaos. Westview.Google Scholar
55. van Veen, L. & Kawahara, G. 2011 Homoclinic tangle on the edge of shear turbulence. Phys. Rev. Lett. 107 (11), 114501.Google Scholar
56. Viswanath, D. 2006 Recurrent motions within plane-Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
57. Viswanath, D. 2009 The critical layer in pipe flow at high Reynolds number. Phil. Trans. R. Soc. Lond. A 367 (1888), 561–576.Google Scholar
58. Vollmer, J., Schneider, T. M. & Eckhardt, B. 2009 Basin boundary, edge of chaos and edge state in a two-dimensional model. New J. Phys. 11, 013040.CrossRefGoogle Scholar
59. Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98 (20), 204501.Google Scholar
60. Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
61. Willis, A. P. & Kerswell, R. R. 2008 Coherent structures in localized and global pipe turbulence. Phys. Rev. Lett. 100 (12).Google Scholar
62. Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59, 281–335.CrossRefGoogle Scholar
63. Wygnanski, I. J., Sokolov, M. & Friedman, D. 1975 On transition in a pipe. Part 2. The equilibrium puff. J. Fluid Mech. 69, 283–304.Google Scholar
64. Zikanov, O. Y. 1996 On the instability of pipe Poiseuille flow. Phys. Fluids 8 (11), 2923–2932.Google Scholar

F. Mellibovsky and B. Eckhardt supplementary movies

Modulated travelling wave (mtw) at Re=2335, κ=1.63. Top left: Phase map projection. Top right: axial phase speed (cz, red) and mean axial pressure gradient ((∇p)z, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ 〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle-(tw) and upper-middle-branch (tw2) travelling.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 3.2 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Modulated travelling wave (mtw) at Re=2335, κ=1.63. Top left: Phase map projection. Top right: axial phase speed (cz, red) and mean axial pressure gradient ((∇p)z, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ 〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle-(tw) and upper-middle-branch (tw2) travelling.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 1.7 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Modulated spiralling wave (msw) at Re=2185, κ=1.63. Top left: Phase map projection. The projection on the horizontal plane corresponds to a projection on the shift-reflect subspace. Top right: axial (cz, red) and azimuthal phase speed (c&theta, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle- (tw) and upper-middle-branch (tw2) travelling-wave values are indicated alongside lower-branch spiralling-wave (sw) values for reference.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 3.4 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Modulated spiralling wave (msw) at Re=2185, κ=1.63. Top left: Phase map projection. The projection on the horizontal plane corresponds to a projection on the shift-reflect subspace. Top right: axial (cz, red) and azimuthal phase speed (c&theta, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle- (tw) and upper-middle-branch (tw2) travelling-wave values are indicated alongside lower-branch spiralling-wave (sw) values for reference.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 1.6 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Doubly-modulated spiralling wave (m2sw) at Re=2205, κ=1.63. Top left: Phase map projection. The projection on the horizontal plane corresponds to a projection on the shift-reflect subspace. Top right: axial (cz, red) and azimuthal phase speed (c&theta, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle- (tw) and upper-middle-branch (tw2) travelling-wave values are indicated alongside lower-branch spiralling-wave (sw) values for reference.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 7.9 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Doubly-modulated spiralling wave (m2sw) at Re=2205, κ=1.63. Top left: Phase map projection. The projection on the horizontal plane corresponds to a projection on the shift-reflect subspace. Top right: axial (cz, red) and azimuthal phase speed (c&theta, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle- (tw) and upper-middle-branch (tw2) travelling-wave values are indicated alongside lower-branch spiralling-wave (sw) values for reference.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 3 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Mildly chaotic spiralling wave (cw) at Re=2205, κ=1.63. Top left: Phase map projection. The projection on the horizontal plane corresponds to a projection on the shift-reflect subspace. Top right: axial (cz, red) and azimuthal phase speed (c&theta, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle- (tw) and upper-middle-branch (tw2) travelling-wave values are indicated alongside lower-branch spiralling-wave (sw) values for reference.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 19.3 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Mildly chaotic spiralling wave (cw) at Re=2205, κ=1.63. Top left: Phase map projection. The projection on the horizontal plane corresponds to a projection on the shift-reflect subspace. Top right: axial (cz, red) and azimuthal phase speed (c&theta, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle- (tw) and upper-middle-branch (tw2) travelling-wave values are indicated alongside lower-branch spiralling-wave (sw) values for reference.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 7.3 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Unstable modulated travelling wave (umtw) at Re=2209.67, κ=1.63. Top left: Phase map projection. Top right: axial phase speed (cz, red) and mean axial pressure gradient ((∇p)z, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle- (tw) and upper-middle-branch (tw2) travelling-wave values are indicated for reference.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 3.3 MB

F. Mellibovsky and B. Eckhardt supplementary movies

Unstable modulated travelling wave (umtw) at Re=2209.67, κ=1.63. Top left: Phase map projection. Top right: axial phase speed (cz, red) and mean axial pressure gradient ((∇p)z, blue) along a full period. Bottom left: z-averaged axial velocity contours relative to the parabolic profile (contour spacing: Δ〈uz〉z=0.1 U) with in-plane velocity vectors. Bottom right: Axial vorticity iso-surfaces at ωz= ±1.0 U/D. Blue for negative, red for positive. Lower-middle- (tw) and upper-middle-branch (tw2) travelling-wave values are indicated for reference.

Download F. Mellibovsky and B. Eckhardt supplementary movies(Video)
Video 1.5 MB