Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T16:53:27.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Free-surface jet flow of a shear-thinning power-law fluid near the channel exit

Published online by Cambridge University Press:  01 May 2014

Roger E. Khayat
Roger E. Khayat*
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, Canada N6A 5B9
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The jet flow of a shear-thinning power-law fluid is examined theoretically as it emerges from a channel at moderate Reynolds number. Poiseuille flow conditions are assumed to prevail far upstream from the exit. The problem is solved using the method of matched asymptotic expansions. A similarity solution is obtained in the inner layer near the free surface, with the outer layer extending to the jet centreline. An inner thin viscous sublayer is introduced to smooth out the singularity in viscosity at the free surface, allowing the inner algebraically decaying solutions to be matched smoothly with the solution near the free surface. A Newtonian jet is found to contract more than a shear-thinning jet. While both the inner-layer thickness and the free-surface height are 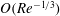$O(\mathit{Re}^{-1/3})$, and grow with downstream distance, the sublayer thickness is smaller, 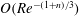$O(\mathit{Re}^{-(1+n)/3})$, growing with distance for 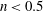$n < 0.5$, and decaying for 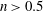$n > 0.5$. The relaxation downstream distance for the jet is found to grow logarithmically with 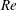$\mathit{Re}$.

JFM classification

Boundary Layers: Boundary Layers Non-Newtonian Flows: Non-Newtonian Flows Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 580 - 617
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A., Shah, M. & Petersen, E. E. 1960 Momentum and heat transfer in laminar boundary-layer flows of non-Newtonian fluids past external surface. AIChE J. 6, 312.Google Scholar
Andersson, H. I., Aarseth, J. B., Braud, N. & Dandapat, B. S. 1996 Flow of a power-law fluid film over an unsteady stretching surface. J. Non-Newtonian Fluid Mech. 62, 1.CrossRefGoogle Scholar
Andersson, H. I. & Irgens, F. 1988 Gravity-driven laminar film flow of power-law fluids along vertical walls. J. Non-Newtonian Fluid Mech. 27, 153.CrossRefGoogle Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 2002 Transport Phenomena. John Wiley & Sons, Inc.Google Scholar
Bowles, R. I. & Smith, F. T. 1992 The standing hydraulic jump: theory, computations and comparisons with experiments. J. Fluid Mech. 242, 145.Google Scholar
Brown, S. N. & Stewartson, K. 1965 On similarity solutions of the boundary-layer equations with algebraic decay. J. Fluid Mech. 23, 673.CrossRefGoogle Scholar
Bush, J. W. M. & Aristoff, J. M. 2003 The influence of surface tension on the circular hydraulic jump. J. Fluid Mech. 489, 229.CrossRefGoogle Scholar
Chapman, S. J., Fitt, A. D. & Picase, C. P. 1997 Extrusion of power-law shear-thinning fluids with small exponent. Intl J. Numer. Meth. Fluids 32, 187.Google Scholar
Denier, J. P. & Dabrowski, P. P. 2004 On the boundary-layer equations for power-law fluids. Proc. R. Soc. Lond. A 460, 3143.Google Scholar
Denier, J. P. & Hewitt, R. E. 2004 Asymptotic matching constraints for a boundary-layer flow of a power-law fluid. J. Fluid Mech. 518, 261.Google Scholar
Ellwood, K. R. J., Georgiou, G. C., Papanastasiou, T. C. & Wilkes, J. O. 1990 Laminar jets of Bingham-plastic liquids. J. Rheol. 34, 787.CrossRefGoogle Scholar
Gabbanelli, S., Drazer, G. & Koplik, J. 2005 Lattice Boltzmann method for non-Newtonian (power-law) fluids. Phys. Rev. E 72, 046312.Google Scholar
Goldstein, S. 1960 Lectures in Fluid Mechanics. Interscience, New York.Google Scholar
Goren, S. L. & Wronski, S. 1966 The shape of low-speed capillary jets of Newtonian liquids. J. Fluid Mech. 25, 185.CrossRefGoogle Scholar
Gorla, R. S. R. 1977 Laminar swirling power-law non-Newtonian fluid jet impinging on a normal plane. J. Non-Newtonian Fluid Mech. 2, 299.Google Scholar
Green, R. G. & Griskey, R. G. 1968 Rheological behaviour of dilatant (shear-thickening) fluids. Part I. Experimental and data. Trans. Soc. Rheol. 12 (1), 13.Google Scholar
Khayat, R. E. & Kim, K. 2006 Thin-film flow of a viscoelastic fluid on an axisymmetric substrate of arbitrary shape. J. Fluid Mech. 552, 37.CrossRefGoogle Scholar
Lee, S. Y. & Ames, W. F. 1966 Similarity solutions for non-Newtonian fluids. Am. Inst. Chem. Engrs J. 6, 700.CrossRefGoogle Scholar
Li, L., Papadopolous, D. P., Smith, F. T. & Wu, G. X. 2002 Rapid plunging of a body partly submerged in water. J. Engng Maths 42, 303.CrossRefGoogle Scholar
Liao, S. 2003 On the analytic solution of magnetohydrodynamic flows of non-Newtonian fluids over a stretching sheet. J. Fluid Mech. 488, 189.CrossRefGoogle Scholar
Lindner, A., Bonn, D. & Meunier, J. 2000 Viscous fingering in a shear-thinning fluid. Phys. Fluids 12, 256.CrossRefGoogle Scholar
Miladinova, S., Lebon, G. & Toshev, E. 2004 Thin-film flow of power-law liquid falling down an inclined plate. J. Non-Newtonian Fluid Mech. 122, 69.CrossRefGoogle Scholar
Mire, C. A., Agrawal, A., Wallace, G. G., Calvert, P. & Panhuis, M. 2011 Inkjet and extrusion printing of conducting poly(3,4-ethylenedioxythiophene) tracks on and embedded in biopolymer materials. J. Mater. Chem. 21, 2671.Google Scholar
Miyake, Y., Yukai, E. & Iemoto, Y. 1979 On a two-dimensional laminar liquid jet. Bull. Japan Soc. Mech. Engrs. 22, 1382.CrossRefGoogle Scholar
Ng, C. & Mei, C. C. 1994 Roll waves on a shallow layer of mud modelled as a power-law fluid. J. Fluid Mech. 263, 151.Google Scholar
Omodei, B. J. 1979 Computer solutions of a plane Newtonian jet with surface tension. Comput. Fluids 7, 79.Google Scholar
Pegler, S. S., Lister, J. R. & Worster, M. G. 2012 Release of a viscous power-law fluid over an inviscid ocean. J. Fluid Mech. 700, 63.Google Scholar
Phares, D. J., Smedley, G. T. & Flagan, R. C. 2000 The wall shear stress produced by the normal impingement of a jet on a flat surface. J. Fluid Mech. 418, 351.CrossRefGoogle Scholar
Philippe, C. & Dumargue, P. 1991 Étude de l’établissement d’un jet liquide laminaire émergeant d’une conduite cylindrique verticale semi-infinie et soumis á l’influence de la gravité. Z. Angew. Math. Phys. 42, 227.CrossRefGoogle Scholar
Poole, R. J. & Ridley, B. S. 2007 Development-length requirements for fully developed laminar pipe flow of inelastic non-Newtonian liquids. J. Fluids Engng 129, 1281.Google Scholar
Ruschak, K. J. & Scriven, L. E. 1977 Developing flow on a vertical wall. J. Fluid Mech. 81, 305.Google Scholar
Saffari, A. & Khayat, R. E. 2009 Flow of viscoelastic jet with moderate inertia near channel exit. J. Fluid Mech. 639, 65.Google Scholar
Saprykin, S., Koopmans, R. J. & Kalliadasis, S. 2007 Free-surface thin-film flows over topography: influence of inertia and viscoelasticity. J. Fluid Mech. 578, 271.CrossRefGoogle Scholar
Sayag, R. & Worster, G. E. 2013 Axisymmetric gravity currents of power-law fluids over a rigid horizontal surface. J. Fluid Mech. 716, R5.Google Scholar
Schowalter, W. R. 1960 The application of boundary-layer theory to power-law Pseudoplastic fluids: similar solutions. Am. Inst. Chem. Engrs J. 6, 24.CrossRefGoogle Scholar
Smith, F. T. 1976a Flow through constricted or dilated pipes and channels: part 1. Q. J. Mech. Appl. Maths 29, 343.Google Scholar
Smith, F. T. 1976b Flow through constricted or dilated pipes and channels: part 2. Q. J. Mech. Appl. Maths 29, 365.CrossRefGoogle Scholar
Smith, F. T. 1979 The separating flow through a severely constricted symmetric tube. J. Fluid Mech. 90, 725.CrossRefGoogle Scholar
Sobey, I. J. 2005 Interactive Boundary Layer Theory. Oxford University Press.Google Scholar
Tadmor, Z. & Gogos, C. G. 1979 Die forming. In Principles of Polymer Processing, John Wiley & Sons.Google Scholar
Tillett, J. P. K. 1968 On the laminar flow in a free jet of liquid at high Reynolds numbers. J. Fluid Mech. 32, 273.Google Scholar
Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. Parabolic Press.Google Scholar
Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29.CrossRefGoogle Scholar
Weinstein, S. J., Ruschak, K. J. & Ng, K. C. 2003 Developing flow of a power-law liquid film on an inclined plane. Phys. Fluids 15, 2973.Google Scholar
Wilson, D. E. 1986 A similarity solution for axisymmetric viscous-gravity jet. Phys. Fluids 29 (3), 632.CrossRefGoogle Scholar
Wu, J. & Thompson, M. C. 1996 Non-Newtonian shear-thinning flows past a flat plate. J. Non-Newtonian Fluid Mech. 66, 127.CrossRefGoogle Scholar
Yaruso, B. 1991 Exit and entrance flows of non-Newtonian fluids in parallel slits. J. Non-Newtonian Fluid Mech. 40, 103.CrossRefGoogle Scholar
Zhao, J. & Khayat, R. E. 2008 Spread of a non-Newtonian liquid jet over a horizontal plate. J. Fluid Mech. 613, 411.Google Scholar