Published online by Cambridge University Press: 15 November 2016
Large eddy simulation (LES) is used to study the evolution and structure of a lock-exchange, Boussinesq gravity current forming in a channel partially blocked by a porous layer. This configuration is used to understand how the characteristics of a surface layer containing floating vegetation affects the generation of thermally driven convective water exchange in a long shallow channel. The porous layer, which represents the roots of the floating vegetation, contains a staggered array of rigid square cylinders of edge length 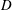 $D$ with solid volume fraction
$D$ with solid volume fraction 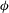 $\unicode[STIX]{x1D719}$. The cylinders extend over a depth
$\unicode[STIX]{x1D719}$. The cylinders extend over a depth 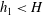 $h_{1}<H$ below the free surface, where
$h_{1}<H$ below the free surface, where 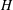 $H$ is the channel depth. The surface current of lighter fluid splits into two layers, one propagating slowly inside the porous layer and the other flowing beneath the porous layer. The main geometrical parameters of the porous layer,
$H$ is the channel depth. The surface current of lighter fluid splits into two layers, one propagating slowly inside the porous layer and the other flowing beneath the porous layer. The main geometrical parameters of the porous layer, 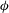 $\unicode[STIX]{x1D719}$ and
$\unicode[STIX]{x1D719}$ and 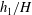 $h_{1}/H$, have a large effect on the dynamics and structure of the surface current and the temporal variation of the front position. For cases with sufficiently large values of
$h_{1}/H$, have a large effect on the dynamics and structure of the surface current and the temporal variation of the front position. For cases with sufficiently large values of 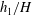 $h_{1}/H$ and
$h_{1}/H$ and 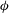 $\unicode[STIX]{x1D719}$, the front within the porous layer approaches the triangular shape observed for low Reynolds number lock-exchange currents propagating in a channel containing cylinders over its whole volume (
$\unicode[STIX]{x1D719}$, the front within the porous layer approaches the triangular shape observed for low Reynolds number lock-exchange currents propagating in a channel containing cylinders over its whole volume (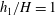 $h_{1}/H=1$), and the surface current transitions to a drag-dominated regime in which the front velocity is proportional to
$h_{1}/H=1$), and the surface current transitions to a drag-dominated regime in which the front velocity is proportional to 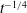 $t^{-1/4}$, where
$t^{-1/4}$, where  $t$ is the time since the current is initiated. For sufficiently high values of
$t$ is the time since the current is initiated. For sufficiently high values of 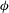 $\unicode[STIX]{x1D719}$, the velocity of the fluid inside the porous layer is close to zero at all locations except for those situated close to the lock gate and for some distance behind the front. Close to the front, lighter fluid from below penetrates into the porous layer due to unstable stratification at the bottom of the porous layer. Simulation results are also used to assess how
$\unicode[STIX]{x1D719}$, the velocity of the fluid inside the porous layer is close to zero at all locations except for those situated close to the lock gate and for some distance behind the front. Close to the front, lighter fluid from below penetrates into the porous layer due to unstable stratification at the bottom of the porous layer. Simulation results are also used to assess how  $\unicode[STIX]{x1D719},h_{1}/H$ and the Reynolds number affect the rate at which the heavier fluid situated initially inside the porous layer is removed by the advancing surface current and the main mixing mechanisms. Based on the estimated time scales for flushing the porous (root) layer, we show that flushing can significantly enhance the overall rate of nutrient removal by the floating vegetation by maintaining a higher concentration of nutrients within the root layer.
$\unicode[STIX]{x1D719},h_{1}/H$ and the Reynolds number affect the rate at which the heavier fluid situated initially inside the porous layer is removed by the advancing surface current and the main mixing mechanisms. Based on the estimated time scales for flushing the porous (root) layer, we show that flushing can significantly enhance the overall rate of nutrient removal by the floating vegetation by maintaining a higher concentration of nutrients within the root layer.
Effect of solid volume fraction. Current is visualized based on nondimensional density (top three frames φ=8%, 16% and 24%) and spanwise vorticity fields (next three frames). Bottom two frames shows a zoom of the concentration field.
Effect of depth of porous layer. Current is visualized based on nondimensional density (top three frames corresponding to a relative height of the porous layer h1/H=0.1, 0.27 and 0.5) and spanwise vorticity (next three frames) fields. The bottom frames show a detailed view of the concentration field
Effect of Reynolds number. Current is visualized based on nondimensional density (top two frames showing Re=5,700 and Re=500,000 cases) and spanwise vorticity fields (next two frames). The bottom 4 frames show a detailed view of the concentration and vorticity fields.