Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T07:35:44.072Z Has data issue: false hasContentIssue false
  • English
  • Français

Free-stream coherent structures in parallel boundary-layer flows

Published online by Cambridge University Press:  09 July 2014

Kengo Deguchi  and
Philip Hall
Kengo Deguchi*
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
Philip Hall
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Our concern in this paper is with high-Reynolds-number nonlinear equilibrium solutions of the Navier–Stokes equations for boundary-layer flows. Here we consider the asymptotic suction boundary layer (ASBL) which we take as a prototype parallel boundary layer. Solutions of the equations of motion are obtained using a homotopy continuation from two known types of solutions for plane Couette flow. At high Reynolds numbers, it is shown that the first type of solution takes the form of a vortex–wave interaction (VWI) state, see Hall & Smith (J. Fluid Mech., vol. 227, 1991, pp. 641–666), and is located in the main part of the boundary layer. 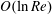On the other hand, here the second type is found to support an equilibrium solution of the unit-Reynolds-number Navier–Stokes equations in a layer located a distance of $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}O(\ln \mathit{Re})$ from the wall. Here 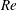$\mathit{Re}$ is the Reynolds number based on the free-stream speed and the unperturbed boundary-layer thickness. The streaky field produced by the interaction grows exponentially below the layer and takes its maximum size within the unperturbed boundary layer. The results suggest the possibility of two distinct types of streaky coherent structures existing, possibly simultaneously, in disturbed boundary layers.

JFM classification

Boundary Layers: Boundary Layers Mathematical Foundations: Mathematical Foundations Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 602 - 625
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: School of Mathematics, Monash University, Melbourne, VIC 3800, Australia.

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary-layer. J. Fluid Mech. 422, 1–54.Google Scholar
Blackburn, H. M., Hall, P. & Sherwin, S. J. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 721, 58–85.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Deguchi, K.2013 Finite amplitude solutions in sliding Couette flow. PhD thesis, Department of Aeronautics, Kyoto University, Japan.Google Scholar
Deguchi, K. & Hall, P. 2014 The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.Google Scholar
Deguchi, K., Hall, P. & Walton, A. G. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.Google Scholar
Deguchi, K. & Walton, A. G. 2013 A swirling spiral wave solution in pipe flow. J. Fluid Mech. 737, R2.Google Scholar
Dong, M. & Wu, X. 2013 On continuous spectra of the Orr–Sommerfeld/Squire equations and entrainment of free-stream vortical disturbances. J. Fluid Mech. 732, 616–659.Google Scholar
Duck, P. W., Ruban, A. I. & Zhikharev, C. N. 1996 The generation of Tollmien–Schlichting waves by free-stream turbulence. J. Fluid Mech. 312, 341–371.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Fransson, J. H. M. & Alfredsson, P. H. 2003 On the disturbance growth in an asymptotic suction boundary-layer. J. Fluid Mech. 482, 51–90.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1989 Nonlinear Tollmien–Schlichting/vortex interaction in boundary-layers. Eur. J. Mech. (B/Fluids) 8 (3), 179–205.Google Scholar
Hall, P. & Smith, F. T. 1990 Near planar TS waves and longitudinal vortices in channel flow: nonlinear interaction and focussing. In Instability and Transition (ed. Hussaini, M. Y.), pp. 5–39. Springer.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.CrossRefGoogle Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–337.Google Scholar
Herbert, T. 1988 Secondary instability of boundary layers. Annu. Rev. Fluid Mech. 20, 487–526.Google Scholar
Hocking, L. M. 1975 Nonlinear instability of the asymptotic suction velocity profile. Q. J. Mech. Appl. Maths 28, 341–353.Google Scholar
Itano, T. & Generalis, S. C. 2009 Hairpin vortex solution in planar Couette flow: a tapestry of knotted vortices. Phys. Rev. Lett. 102, 114501.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.Google Scholar
Jimenez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Khapko, T., Kreilos, T., Schlatter, P., Duguet, Y., Eckhardt, B. & Henningson, D. S. 2012 Localized edge states in the asymptotic suction boundary layer. J. Fluid Mech. 717, R6.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Klein, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary-layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kreilos, T. & Eckhardt, B. 2012 Periodic orbits near onset of chaos in plane Couette flow. Chaos 22, 047505.Google Scholar
Kreilos, T., Veble, G., Schneider, T. M. & Eckhardt, B. 2013 Edge states for the turbulent transition in the asymptotic suction boundary layer. J. Fluid Mech. 726, 100–122.Google Scholar
Milinazzo, F. A. & Saffman, P. G. 1985 Finite-amplitude steady waves in plane viscous shear flows. J. Fluid Mech. 160, 281–295.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Rao, K. N., Narasimha, R. & Narayanan, M. A. B. 1971 The ‘bursting’ phenomenon in a turbulent boundary-layer. J. Fluid Mech. 48, 339–352.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary-layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Schlatter, P. & Örlü, B. 2011 Turbulent asymptotic suction boundary layers studied by simulation. J. Phys.: Conf. Ser. 318, 022020.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.Google Scholar
Smith, F. T. & Bodonyi, R. J. 1982 Amplitude-dependent neutral modes in the Hagen–Poiseuille flow through a circular pipe. Proc. R. Soc. Lond. A 384, 463–489.Google Scholar
Smith, F. T., Doorly, D. J. & Rothmayer, A. P. 1990 On displacement-thickness, wall-layer and mid-flow scales in turbulent boundary layers, and slugs of vorticity in channel and pipe flows. Proc. R. Soc. Lond. A 428, 255–281.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.Google Scholar
Yoshioka, S., Fransson, J. H. M. & Alfredsson, P. H. 2004 Free stream turbulence induced disturbances in boundary layers with wall suction. Phys. Fluids 16, 3530–3539.Google Scholar