Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-25T20:17:12.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Freely rising or falling of a sphere in a square tube at intermediate Reynolds numbers

Published online by Cambridge University Press:  02 December 2024

Deming Nie Open the ORCID record for Deming Nie [Opens in a new window] ,
Jingwen Wang ,
Siwen Li  and
Jianzhong Lin Open the ORCID record for Jianzhong Lin [Opens in a new window]
Deming Nie
Affiliation:
College of Metrology Measurement and Instrument, China Jiliang University, Hangzhou 310018, China
Jingwen Wang
Affiliation:
College of Metrology Measurement and Instrument, China Jiliang University, Hangzhou 310018, China
Siwen Li
Affiliation:
College of Metrology Measurement and Instrument, China Jiliang University, Hangzhou 310018, China
Jianzhong Lin*
Affiliation:
Key Laboratory of Impact and Safety Engineering (Ningbo University), Ministry of Education, Ningbo 315201, China Institute of Fluid Engineering, Zhejiang University, Hangzhou 310027, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

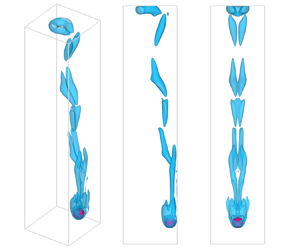
The motion of a sphere freely rising or falling in a 5d (d is the diameter of the sphere) square tube was numerically studied for the sphere-to-fluid density ratio ranging from 0.1 to 2.3 (0.1 ≤ ρs/ρ ≤ 2.3, ρs is the density of spheres and ρ the fluid density) and Galileo number from 140 to 230 (140 ≤ Ga ≤ 230). We report that Hopf bifurcation occurs at Gacrit ≈ 157, where both the heavy and light spheres lose stability. The helical motion is widely seen for all spheres at Ga > 160 resulting from a double-threaded vortex interacting with the tube walls, which becomes irregular at Ga ≥ 190 where heavy spheres act differently from their counterparts; that is, heavy spheres change their helical directions alternately while light spheres exhibit helical trajectories with jaggedness in connection with the shedding of the double-threaded vortices. This is because of the difference in inertia between the heavy and light spheres. We also checked the oscillation periods for the helical motion of the spheres. They show opposite variations with ρs/ρ for the two types of spheres. Light spheres (ρs/ρ ≤ 0.7) reach a zigzagging regime at Ga ≥ 200 where a vortex loop (hairpin-like vortical structure) is formed which may develop into a vortex ring downstream at small ρs/ρ. This might be the first time a transition from the helical motion to the zigzagging motion for heavy spheres (ρs/ρ ≥ 1.8) has been reported. Finally, we examined the dependence of both the terminal Reynolds number and the drag coefficient of the spheres on the Galileo number.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A82
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aidun, C.K., Lu, Y. & Ding, E. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.CrossRefGoogle Scholar
Auguste, F. & Magnaudet, J. 2018 Path oscillations and enhanced drag of light rising spheres. J. Fluid Mech. 841, 228–266.CrossRefGoogle Scholar
Bagchi, P. & Balachandar, S. 2002 Shear versus vortex-induced lift force on a rigid sphere at moderate Re. J. Fluid Mech. 473, 379–388.CrossRefGoogle Scholar
Brown, P.P. & Lawler, D.F. 2003 Sphere drag and settling velocity revisited. J. Environ. Engng 129, 222–231.CrossRefGoogle Scholar
Cabrera-Booman, F., Plihon, N. & Bourgoin, M. 2024 Path instabilities and drag in the settling of single spheres. Intl J. Multiphase Flow 171, 104664.CrossRefGoogle Scholar
Chrust, M., Goujon-Durand, S. & Wesfreid, J.E. 2013 Loss of a fixed plane of symmetry in the wake of a sphere. J. Fluids Struct. 41, 51–56.CrossRefGoogle Scholar
Daniel, W.B., Ecke, R.E., Subramanian, G. & Koch, D.L. 2009 Clusters of sedimenting high Reynolds number particles. J. Fluid Mech. 625, 371–385.CrossRefGoogle Scholar
Deloze, T., Hoarau, Y. & Dušek, J. 2012 Transition scenario of a sphere freely falling in a vertical tube. J. Fluid Mech. 711, 40–60.CrossRefGoogle Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20, 051702.CrossRefGoogle Scholar
Fabre, D., Tchoufag, J. & Magnaudet, J. 2012 The steady oblique path of buoyancy-driven disks and spheres. J. Fluid Mech. 707, 24–36.CrossRefGoogle Scholar
Feng, Z., Gatewood, J. & Michaelides, E.E. 2021 Wall effects on the flow dynamics of a rigid sphere in motion. ASME J. Fluids Engng 143, 081106.CrossRefGoogle Scholar
Ghidersa, B. & Dušek, J. 2000 Breaking of axisymmetry and onset of unsteadiness in the wake of a sphere. J. Fluid Mech. 423, 33–69.CrossRefGoogle Scholar
Horowitz, M. & Williamson, C.H.K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.CrossRefGoogle Scholar
Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Johnson, T. & Patel, V. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
Kajishima, T. 2004 Influence of particle rotation on the interaction between particle clusters and particle-induced turbulence. Intl J. Heat Fluid Flow 25, 721–728.CrossRefGoogle Scholar
Karamanev, D.G., Chavarie, C. & Mayer, R.C. 1996 Dynamics of the free rise of a light solid sphere in liquid. AIChE J. 42, 1789–1792.CrossRefGoogle Scholar
Karamanev, D.G. & Nikolov, L.N. 1992 Free rising spheres do not obey Newton's law for free settling. AIChE J. 38, 1843–1846.CrossRefGoogle Scholar
Lallemand, P. & Luo, L.S. 2003 Lattice Boltzmann method for moving boundaries. J. Comput. Phys. 184, 406–421.CrossRefGoogle Scholar
Magarvey, R.H. & Bishop, R.L. 1961 Transition ranges for three-dimensional wakes. Can. J. Phys. 39, 1418–1422.CrossRefGoogle Scholar
Matas, J.P., Morris, J.F. & Guazzelli, E. 2004 Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 515, 171–195.CrossRefGoogle Scholar
Mei, R., Yu, D., Shyy, W. & Luo, L.-S. 2002 Force evaluation in the lattice Boltzmann method involving curved geometry. Phys. Rev. E 65, 041203.CrossRefGoogle ScholarPubMed
Mittal, R. 1999 Planar symmetry in the unsteady wake of a sphere. AIAA J. 37, 388–390.CrossRefGoogle Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.CrossRefGoogle Scholar
Nie, D. & Lin, J. 2019 Discontinuity in the sedimentation system with two particles having different densities in a vertical channel. Phys. Rev. E 99, 053112.CrossRefGoogle Scholar
Nie, D. & Lin, J. 2020 Simulation of sedimentation of two spheres with different densities in a square tube. J. Fluid Mech. 896, A12.CrossRefGoogle Scholar
Nie, D., Ying, Y., Guan, G., Lin, J. & Ouyang, Z. 2023 Two-dimensional study on the motion and interactions of squirmers under gravity in a vertical channel. J. Fluid Mech. 960, A31.CrossRefGoogle Scholar
Ormières, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83, 80–83.CrossRefGoogle Scholar
Peng, C., Teng, Y., Hwang, B., Guo, Z. & Wang, L.-P. 2016 Implementation issues and benchmarking of lattice Boltzmann method for moving rigid particle simulations in a viscous flow. Comput. Maths Applics. 72, 349–374.CrossRefGoogle Scholar
Qian, Y.H. 1992 Lattice BGK models for Navier–Stokes equation. Europhys. Lett. 17, 479–484.CrossRefGoogle Scholar
Raaghav, S.K.R., Poelma, C. & Breugem, W.P. 2022 Path instabilities of a freely rising or falling sphere. Intl J. Multiphase Flow 153, 104111.CrossRefGoogle Scholar
Sakamoto, H. & Haniu, H. 1995 The formation mechanism and shedding frequency of vortices from a sphere in uniform shear flow. J. Fluid Mech. 287, 151–171.CrossRefGoogle Scholar
Segrè, G. & Silberberg, A. 1961 Radial Poiseuille flow of suspensions. Nature 189, 209–210.CrossRefGoogle Scholar
Shi, P., Rzehak, R., Lucas, D. & Magnaudet, J. 2021 Drag and lift forces on a rigid sphere immersed in a wall-bounded linear shear flow. Phys. Rev. Fluids 6, 104309.CrossRefGoogle Scholar
Tomboulides, A.G. & Orszag, S.A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.CrossRefGoogle Scholar
Turton, R. & Levenspiel, O. 1986 A short note on the drag correlation for spheres. Powder Technol. 47, 83–86.CrossRefGoogle Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.CrossRefGoogle Scholar
Uhlmann, M. & Dušek, J. 2014 The motion of a single heavy sphere in ambient fluid: a benchmark for interface-resolved particulate flow simulations with significant relative velocities. Intl J. Multiphase Flow 59, 221–243.CrossRefGoogle Scholar
Veldhuis, C.H.J. & Biesheuvel, A. 2007 An experimental study of the regimes of motion of spheres falling or ascending freely in a Newtonian fluid. Intl J. Multiphase Flow 33, 1074–1087.CrossRefGoogle Scholar
Veldhuis, C.H.J., Biesheuvel, A. & Lohse, D. 2009 Freely rising light solid spheres. Intl J. Multiphase Flow 35, 312–322.CrossRefGoogle Scholar
Will, J.B. & Krug, D. 2021 a Dynamics of freely rising spheres: the effect of moment of inertia. J. Fluid Mech. 927, A7.CrossRefGoogle Scholar
Will, J.B. & Krug, D. 2021 b Rising and sinking in resonance: mass distribution critically affects buoyancy-driven spheres via rotational dynamics. Phys. Rev. Lett. 126, 174502.CrossRefGoogle ScholarPubMed
Yang, B.H., Wang, J., Joseph, D.D., Hu, H.H., Pan, T.W. & Glowinski, R. 2005 Migration of a sphere in tube flow. J. Fluid Mech. 540, 109–131.CrossRefGoogle Scholar
Yu, Z., Phan-Thien, N. & Tanner, R.I. 2004 Dynamic simulation of sphere motion in a vertical tube. J. Fluid Mech. 518, 61–93.CrossRefGoogle Scholar
Zeng, L., Balachandar, S. & Fischer, P. 2005 Wall-induced forces on a rigid sphere at finite Reynolds number. J. Fluid Mech. 536, 1–25.CrossRefGoogle Scholar
Zhao, H., Liu, X., Li, D., Wei, A., Luo, K. & Fan, J. 2016 Vortex dynamics of a sphere wake in proximity to a wall. Intl J. Multiphase Flow 79, 88–106.CrossRefGoogle Scholar
Zhou, W. & Dušek, J. 2015 Chaotic states and order in the chaos of the paths of freely falling and ascending spheres. Intl J. Multiphase Flow 75, 205–223.CrossRefGoogle Scholar