Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-09T22:03:41.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Formation process of the vortex ring generated by an impulsively started circular disc

Published online by Cambridge University Press:  29 October 2012

An-long Yang ,
Lai-bing Jia  and
Xie-zhen Yin
An-long Yang*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230027, PR China
Lai-bing Jia
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230027, PR China
Xie-zhen Yin
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230027, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an experimental study on the axisymmetric vortex ring generated by a thin circular disc. The velocity and vorticity fields are measured by digital particle image velocimetry (DPIV). The finite-time Lyapunov exponent fields and the Lagrangian coherent structures (LCSs) of the vortex flow are computed in order to analyse the transport of the fluid during its formation and identify the boundary of the vortex ring. The volume, circulation and energy of the vortex ring are calculated. It is found that the formation of the vortex ring basically includes three phases: a rapid growth phase, a stable growth phase and a non-axisymmetric phase. 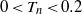In the rapid growth phase (dimensionless time $0\lt {T}_{n} \lt 0. 2$) during which Taylor’s inviscid estimation is valid, the circulation of the vortex ring grows and the translational velocity of the vortex ring decreases. In the stable growth phase (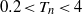$0. 2\lt {T}_{n} \lt 4$), the growth rate of the circulation decreases gradually. In the non-axisymmetric phase (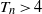${T}_{n} \gt 4$), the ring loses axisymmetry due to instability. Compared with the vortex ring generated by the laminar flow from an orifice, the one generated by a circular disc always moves with the disc, and the entrained fluid decreases and the saturated circulation increases. The temporal impulse exerted by the moving disc on the fluid is estimated by DPIV measurements and is calculated using the direct momentum conservation method. The momentum of the control volume enclosing the LCS is found to occupy 64–68 % of the entire impulse exerted by the disc on the fluid.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Propulsion Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 61 - 85
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Dabiri, J. O. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41, 311–331.CrossRefGoogle Scholar
Dabiri, J. O. & Gharib, M. 2004 Fluid entrainment by isolated vortex rings. J. Fluid Mech. 511, 311–331.Google Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.Google Scholar
Green, M. A., Rowley, C. W. & Haller, G. 2007 Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 572, 111–120.Google Scholar
Haller, G. 2001 Distinguished material surfaces and coherent structures in three-dimensional flows. Physica D 149, 248–277.Google Scholar
Haller, G. 2002 Lagrangian coherent structures from approximate velocity data. Phys. Fluids 14, 1851–1861.Google Scholar
Higuchi, H. & Balligand, H. 1996 Numerical and experimental investigations of the flow over a disk undergoing unsteady motion. J. Fluids Struct. 10, 705–719.Google Scholar
Linden, P. F. & Turner, J. S. 2001 The formation of ‘optimal’ vortex rings, and the efficiency of propulsion devices. J. Fluid Mech. 427, 61–72.Google Scholar
Peng, J., Dabiri, J. O., Madden, P. G. & Lauder, G. V. 2007 Non-invasive measurement of instantaneous forces during aquatic locomotion: a case study of the Bluegill Sunfish pectoral fin. J. Expl Biol. 210, 685–698.Google Scholar
Rosenfeld, M., Rambod, E. & Gharib, M. 1998 Circulation and formation number of laminar vortex ring. J. Fluid Mech. 376, 297–318.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Sallet, D. W. 1975 Impulsive motion of a circular disk which causes a vortex ring. Phys. Fluids 18, 109–111.Google Scholar
Shadden, S. C., Dabiri, J. & Marsden, J. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18, 047105.Google Scholar
Shadden, S. C., Katija, K., Rosenfeld, M., Marsden, J. E. & Dabiri, J. O. 2007 Transport and stirring induced by vortex formation. J. Fluid Mech. 593, 315–331.CrossRefGoogle Scholar
Shadden, S. C., Lekien, F. & Marsden, J. 2005 Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensinal aperiodic flows. Physica D 212, 271–304.Google Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.Google Scholar
Shenoy, A. R. & Kleinstreuer, C. 2008 Flow over a thin circular disk at low to moderate Reynolds numbers. J. Fluid Mech. 605, 253–262.Google Scholar
Taylor, G. I. 1953 Formation of a vortex ring by giving an impulse to a circular disc and then dissolving it away. J. Appl. Phys. 24, 104–105.CrossRefGoogle Scholar
Willert, C. E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10, 181–193.Google Scholar
Wu, J. C. 2005 Elements of Vorticity Aerodynamics. Tsinghua University Press.Google Scholar
Yang, A., Jia, L. & Yin, X. 2010 Experimental study of a starting vortex ring produced by a thin circular disk. J. Biomed. Engng 7, S103–S108.Google Scholar