Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T04:22:27.637Z Has data issue: false hasContentIssue false
  • English
  • Français

Formation of compound droplets during fragmentation of turbulent buoyant oil jet in water

Published online by Cambridge University Press:  04 September 2019

Xinzhi Xue Open the ORCID record for Xinzhi Xue [Opens in a new window]  and
Joseph Katz Open the ORCID record for Joseph Katz [Opens in a new window]
Xinzhi Xue
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Joseph Katz*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

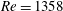Fragmentation of a vertical buoyant silicone oil jet injected into sugar water is elucidated by refractive index matching and planar laser-induced fluorescence. Compound droplets containing multiple water droplets, some with smaller oil droplets, form regularly at jet Reynolds numbers of $Re=1358$ and 2122 and persist for at least up to 30 nozzle diameters. In contrast, they rarely appear at 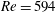$Re=594$. The origin of some of the encapsulated water droplets can be traced back to the entrained water ligaments during the initial roll-up of Kelvin–Helmholtz vortices. Analysis using random forest-based procedures shows that the fraction of compound droplets does not vary significantly with 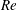$Re$, but increases rapidly with droplet diameter, reaching 78 % for 2 mm droplets. Consequently, the size distributions of compound droplets have peaks that increase in magnitude and shift to a lower diameter with increasing 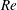$Re$. On average, the interior pockets raise the oil–water interfacial area by 15 %, increasing with diameter and axial location. Also, while the oil droplets are deformed by the jet’s shear field, the interior interfaces remain nearly spherical, consistent with prior studies of the deformation of isolated compound droplets for relevant capillary numbers and viscosity ratio.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 98 - 112
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amiri, A., Larachi, F. & Taghavi, S. M. 2016 Buoyant miscible displacement flows in vertical pipe. Phys. Fluids 28 (10), 102105.Google Scholar
Arganda-Carreras, I., Kaynig, V., Rueden, C., Eliceiri, K. W., Schindelin, J., Cardona, A. & Sebastian Seung, H. 2017 Trainable weka segmentation: a machine learning tool for microscopy pixel classification. Bioinformatics 33 (15), 2424–2426.Google Scholar
Brandvik, PJ., Johansen, Ø, Farooq, U., Angell, G. & Leirvik, F.2014 Subsurface oil releases – experimental study of droplet distributions and different dispersant injection techniques version 2. SINTEF Report No. A26122.Google Scholar
Brandvik, P. J., Johansen, Ø., Leirvik, F., Krause, D. F. & Daling, P. S. 2018 Subsea dispersants injection (SSDI), effectiveness of different dispersant injection techniques – an experimental approach. Mar. Pollut. Bull. 136, 385–393.Google Scholar
Brennen, C. E. 2005 Fundamentals of Multiphase Flow. Cambridge University Press.Google Scholar
Cohen, R. D. 1990 Steady-state cluster size distribution in stirred suspensions. Chem. Soc. Faraday Trans. 86 (12), 2133–2138.Google Scholar
Crounse, B. C., Wannamaker, E. J. & Adams, E. E. 2007 Integral model of a multiphase plume in quiescent stratification. J. Hydraul. Engng 133 (1), 70–76.Google Scholar
Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48 (3), 547–591.Google Scholar
Eggers, J. 1997 Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 69 (3), 865–929.Google Scholar
Gorokhovski, M. & Herrmann, M. 2008 Modeling primary atomization. Annu. Rev. Fluid Mech. 40, 343–366.Google Scholar
Hasnain, A., Segura, E. & Alba, K. 2017 Buoyant displacement flow of immiscible fluids in inclined pipes. J. Fluid Mech. 824, 661–687.Google Scholar
Homma, S., Koga, J., Matsumoto, S., Song, M. & Tryggvason, G. 2006 Breakup mode of an axisymmetric liquid jet injected into another immiscible liquid. Chem. Engng Sci. 61 (12), 3986–3996.Google Scholar
Jarrahbashi, D., Sirignano, W. A., Popov, P. P. & Hussain, F. 2016 Early spray development at high gas density: hole, ligament and bridge formations. J. Fluid Mech. 792, 186–231.Google Scholar
Johansen, Ø., Brandvik, P. J. & Farooq, U. 2013 Droplet breakup in subsea oil releases – part 2: Predictions of droplet size distributions with and without injection of chemical dispersants. Mar. Pollut. Bull. 73 (1), 327–335.Google Scholar
Kim, S. & Dabiri, S. 2017 Transient dynamics of eccentric double emulsion droplets in a simple shear flow. Phys. Rev. Fluids 2 (10), 104305.Google Scholar
Lasheras, J. C. & Hopfinger, E. J. 2000 Liquid jet instability and atomization in a coaxial gas stream. Annu. Rev. Fluid Mech. 32 (1), 275–308.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.Google Scholar
Lin, SP. & Reitz, RD. 1998 Drop and spray formation from a liquid jet. Annu. Rev. Fluid Mech. 30 (1), 85–105.Google Scholar
Mandal, S., Ghosh, U. & Chakraborty, S. 2016 Effect of surfactant on motion and deformation of compound droplets in arbitrary unbounded Stokes flows. J. Fluid Mech. 803, 200–249.Google Scholar
Marmottant, P. & Villermaux, E. 2004 On spray formation. J. Fluid Mech. 498, 73–111.Google Scholar
Martínez-Bazán, C., Montanes, J. L. & Lasheras, J. C. 1999 On the breakup of an air bubble injected into a fully developed turbulent flow. Part 2. Size pdf of the resulting daughter bubbles. J. Fluid Mech. 401, 183–207.Google Scholar
Masutani, S. M. & Adams, E. E. 2001 Experimental study of multi-phase plumes with application to deep ocean oil spills. In Final Report to the US Department of Interior, Minerals Management Service. Hawaii Natural Energy Institute.Google Scholar
Münch, B., Trtik, P., Marone, F. & Stampanoni, M. 2009 Stripe and ring artifact removal with combined wavelet–fourier filtering. Opt. Express 17 (10), 8567–8591.Google Scholar
Murphy, D. W., Xue, X., Sampath, K. & Katz, J. 2016 Crude oil jets in crossflow: effects of dispersant concentration on plume behavior. J. Geophys. Res. 121 (6), 4264–4281.Google Scholar
Shinjo, J. & Umemura, A. 2010 Simulation of liquid jet primary breakup: dynamics of ligament and droplet formation. Intl J. Multiphase Flow 36 (7), 513–532.Google Scholar
Simmons, H. C. 1977 The correlation of drop-size distributions in fuel nozzle sprays. J. Engng Power 99 (3), 309–319.Google Scholar
Smith, K. A., Ottino, J. M. & de la Cruz, M. O. 2004 Encapsulated drop breakup in shear flow. Phys. Rev. Lett. 93 (20), 204501.Google Scholar
Socolofsky, S. A., Adams, E. E. & Sherwood, C. R. 2011 Formation dynamics of subsurface hydrocarbon intrusions following the deepwater horizon blowout. Geophys. Res. Lett. 38 (9), L09602.Google Scholar
Stone, H. A. & Leal, L. G. 1990 Breakup of concentric double emulsion droplets in linear flows. J. Fluid Mech. 211, 123–156.Google Scholar
Villermaux, E. 2007 Fragmentation. Annu. Rev. Fluid Mech. 39, 419–446.Google Scholar
Wu, J., Halter, M., Kacker, R. N., Elliot, J. T. & Plant, A. L.2013 Measurement uncertainty in cell image segmentation data analysis. Tech. Rep. National Institute of Standards and Technology.Google Scholar
Wu, P.-K., Miranda, R. F. & Faeth, G. M. 1995 Effects of initial flow conditions on primary breakup of nonturbulent and turbulent round liquid jets. Atomiz. Sprays 5 (2), 175–196.Google Scholar
Yang, D., Chen, B., Socolofsky, S. A., Chamecki, M. & Meneveau, C. 2016 Large-eddy simulation and parameterization of buoyant plume dynamics in stratified flow. J. Fluid Mech. 794, 798–833.Google Scholar
Zhao, L., Torlapati, J., Boufadel, M. C., King, T., Robinson, B. & Lee, K. 2014 VDROP: A comprehensive model for droplet formation of oils and gases in liquids-incorporation of the interfacial tension and droplet viscosity. Chem. Engng J. 253, 93–106.Google Scholar

Xue and Katz supplementary movie 1

Sample movies of the oil jet fragmentation: left: Re = 594; center: Re = 1358; and right: Re = 2122.

Download Xue and Katz supplementary movie 1(Video)
Video 8.1 MB

Xue and Katz supplementary movie 2

Sample movies of oil ligaments and compound droplets at Re=1358 and z/d = 20.6.

Download Xue and Katz supplementary movie 2(Video)
Video 2.6 MB

Xue and Katz supplementary movie 3

A sample movie showing processes leading to compound droplet formation at Re=1358. Arrows of the same colour follow the same water ligament in frames separated by 2ms.

Download Xue and Katz supplementary movie 3(Video)
Video 4.6 MB

Xue and Katz supplementary movie 4

A sample movie showing the evolution of ligaments resulting in compound droplet formation at Re=1358. The arrows follow the same ligament in frames separated by 2ms.

Download Xue and Katz supplementary movie 4(Video)
Video 592.2 KB