Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T09:13:00.330Z Has data issue: false hasContentIssue false
  • English
  • Français

Formation of a strong negative wake behind a helical swimmer in a viscoelastic fluid

Published online by Cambridge University Press:  16 May 2022

Shijian Wu ,
Tomas Solano ,
Kourosh Shoele Open the ORCID record for Kourosh Shoele [Opens in a new window]  and
Hadi Mohammadigoushki Open the ORCID record for Hadi Mohammadigoushki [Opens in a new window]
Shijian Wu
Affiliation:
Department of Chemical and Biomedical Engineering, FAMU-FSU College of Engineering, Tallahassee, FL 32310, USA
Tomas Solano
Affiliation:
Department of Mechanical Engineering, FAMU-FSU College of Engineering, Tallahassee, FL 32310, USA
Kourosh Shoele
Affiliation:
Department of Mechanical Engineering, FAMU-FSU College of Engineering, Tallahassee, FL 32310, USA
Hadi Mohammadigoushki*
Affiliation:
Department of Chemical and Biomedical Engineering, FAMU-FSU College of Engineering, Tallahassee, FL 32310, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

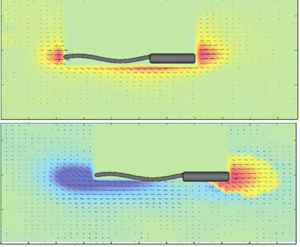
We investigate the effects of helical swimmer shape (i.e. helical pitch angle and tail thickness) on swimming dynamics in a constant viscosity viscoelastic (Boger) fluid via a combination of particle tracking velocimetry, particle image velocimetry and three-dimensional simulations of the finitely extensible nonlinear elastic model with Peterlin approximation (FENE-P). The 3D-printed helical swimmer is actuated in a magnetic field using a custom-built rotating Helmholtz coil. Our results indicate that increasing the swimmer tail thickness and pitch angle enhances the normalized swimming speed (i.e. ratio of swimming speed in the Boger fluid to that of the Newtonian fluid). Strikingly, unlike the Newtonian fluid, the viscoelastic flow around the swimmer is characterized by formation of a front–back flow asymmetry that is characterized by a strong negative wake downstream of the swimmer's body. Evidently, the strength of the negative wake is inversely proportional to the normalized swimming speed. Three-dimensional simulations of the swimmer with the FENE-P model with conditions that match those of experiments, confirm formation of a similar front–back flow asymmetry around the swimmer. Finally, by developing an approximate force balance in the streamwise direction, we show that the contribution of polymer stresses in the interior region of the helix may provide a mechanism for swimming enhancement or diminution in the viscoelastic fluid.

JFM classification

Non-Newtonian Flows: Viscoelasticity Biological Fluid Dynamics: Swimming/flying Aerodynamics: Flow-structure interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , A10
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Angeles, V., Godínez, F.A., Puente-Velazquez, J.A., Mendez-Rojano, R., Lauga, E. & Zenit, R. 2021 a Front-back asymmetry controls the impact of viscoelasticity on helical swimming. Phys. Rev. Fluids 6, 043102.CrossRefGoogle Scholar
Angeles, V., Godínez, F.A., Puente-Velazquez, J.A., Mendez-Rojano, R., Lauga, E. & Zenit, R. 2021 b Front-back asymmetry controls the impact of viscoelasticity on helical swimming. Phys. Rev. Fluids 6 (4), 043102.CrossRefGoogle Scholar
Bansil, R., Celli, J.P., Hardcastle, J.M. & Turner, B.S. 2013 The influence of mucus microstructure and rheology in helicobacter pylori infection. Front. Immunol. 4, 310.CrossRefGoogle ScholarPubMed
Binagia, J.P., Guido, C.S. & Shaqfeh, E.S.G. 2019 Three-dimensional simulations of undulatory and amoeboid swimmers in viscoelastic fluids. Soft Matt. 15, 4836–4855.CrossRefGoogle ScholarPubMed
Binagia, J.P. & Shaqfeh, E.S.G. 2021 Self-propulsion of a freely suspended swimmer by a swirling tail in a viscoelastic fluid. Phys. Rev. Fluids 6, 053301.CrossRefGoogle Scholar
Bird, R.B., Dotson, P.J. & Johnson, N.L. 1980 Polymer solution rheology based on a finitely extensible bead—pring chain model. J. Non-Newtonian Fluid Mech. 7 (2–3), 213–235.CrossRefGoogle Scholar
Das, A., Styslinger, M., Harris, D.M. & Zenit, R. 2021 Force and torque-free helical tail robot to study low Reynolds number microorganism swimming. Rev. Sci. Instrum. 93, 044103.Google Scholar
Dasgupta, M., Liu, B., Fu, H.C., Berhanu, M. & Breuer, K.S. 2013 Speed of a swimming sheet in newtonian and viscoelastic fluids. Phys. Rev. E 87, 013015.CrossRefGoogle ScholarPubMed
Entov, V.M. & Hinch, E.J. 1997 Effect of a spectrum of relaxation times on the capillary thinning of a filament of elastic liquid. J. Non-Newtonian Fluid Mech. 72, 31–53.CrossRefGoogle Scholar
Espinosa-Garcia, J., Lauga, E. & Zenit, R. 2013 Fluid elasticity increases the locomotion of flexible swimmers. Phys. Fluids 25, 031701.CrossRefGoogle Scholar
Fu, H.C., Wolgemuth, C.W. & Powers, T.R. 2007 Theory of swimming filaments in viscoelastic media. Phys. Rev. Lett. 99, 258101–258105.CrossRefGoogle ScholarPubMed
Gómez, S., Godínez, F.A., Lauga, E. & Zenit, R. 2017 Helical propulsion in shear-thinning fluids. J. Fluid Mech. 812, R3.CrossRefGoogle Scholar
Godínez, F.A., Chávez, O. & Zenit, R. 2012 Note: design of a novel rotating magnetic field device. Rev. Sci. Instrum. 83 (6), 066109.CrossRefGoogle ScholarPubMed
Godínez, F.A., Koens, L., Montenegro-Johnson, T.D., Zenit, R. & Lauga, E. 2015 Complex fluids affect low-Reynolds number locomotion in a kinematic-dependent manner. Exp. Fluids 56, 97.CrossRefGoogle Scholar
Gomez, S., Godínez, F.A., Lauga, E. & Zenit, R. 2017 Helical propulsion in shear-thinning fluids. J. Fluid Mech. 812, R3.CrossRefGoogle Scholar
Gray, J. & Hancock, G.J. 1955 The propulsion of Sea-Urchin Spermatozoa. J. Expl Biol. 32 (4), 802–814.CrossRefGoogle Scholar
Housiadas, K.D., Binagia, J.P. & Shaqfeh, E.S.G. 2021 Squirmers with swirl at low Weissenberg number. J. Fluid Mech. 911, A16.CrossRefGoogle Scholar
Kim, M., Bird, J.C., Van Parys, A.J., Breuer, K.S. & Powers, T.R. 2003 A macroscopic scale model of bacterial flagellar bundling. Proc. Natl Acad. Sci. USA 100 (26), 15481–15485.CrossRefGoogle ScholarPubMed
Kroo, L.A., Binagia, J.P., Eckman, N., Prakash, M. & Shaqfeh, E.S.G. 2021 A swimming rheometer: self-propulsion of a freely-suspended swimmer enabled by viscoelastic normal stresses. arXiv:2111.10515.CrossRefGoogle Scholar
Lauga, E. 2007 Propulsion in a viscoelastic fluid. Phys. Fluids 18, 083104.CrossRefGoogle Scholar
Lauga, E. 2020 The Fluid Dynamics of Cell Motility, vol. 62. Cambridge University Press.CrossRefGoogle Scholar
Lauga, E. & Powers, T.R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601.CrossRefGoogle Scholar
Li, G. & Ardekani, A.M. 2015 Undulatory swimming in non-Newtonian fluids. J. Fluid Mech. 784, R4.CrossRefGoogle Scholar
Li, G., Lauga, E. & Ardekani, A.M. 2021 Microswimming in viscoelastic fluids. J. Non-Newtonian Fluid Mech. 297, 104655.CrossRefGoogle Scholar
Liu, B., Powers, T.R. & Breuer, K.S. 2011 Force-free swimming of a model helical flagellum in viscoelastic fluids. Proc. Natl Acad. Sci. USA 108, 19516–19520.CrossRefGoogle Scholar
Martínez, L.E., Hardcastle, J.M., Wang, J., Pincus, Z., Tsang, J., Hoover, T.R., Bansil, R. & Salama, N.R. 2016 Helicobacter pylori strains vary cell shape and flagellum number to maintain robust motility in viscous environments. Mol. Microbiol. 99 (1), 88–110.CrossRefGoogle ScholarPubMed
Ohta, M., Furukawa, T., Yoshida, Y. & Sussman, M. 2019 A three-dimensional numerical study on the dynamics and deformation of a bubble rising in a hybrid Carreau and FENE-CR modeled polymeric liquid. J. Non-Newtonian Fluid Mech. 265, 66–78.CrossRefGoogle Scholar
Omidvar, R., Dalili, A., Mir, A. & Mohammadigoushki, H. 2018 Exploring sensitivity of the extensional flow to wormlike micellar structure. J. Non-Newtonian Fluid Mech. 252, 48–56.CrossRefGoogle Scholar
Omidvar, R., Wu, S. & Mohammadigoushki, H. 2019 Detecting wormlike micellar microstructure using extensional rheology. J. Rheol. 63 (1), 33–44.CrossRefGoogle Scholar
Pak, O.S., Zhu, L., Brandt, L. & Lauga, E. 2012 Micropropulsion and microrheology in complex fluids via symmetry breaking. Phys. Fluids 24 (10), 103102.CrossRefGoogle Scholar
Patteson, A., Gopinath, A., Goulian, M. & Arratia, P.E. 2015 Running and tumbling with E. coli in polymeric solutions. Sci. Rep. 5, 15761.CrossRefGoogle Scholar
Patteson, A.E., Gopinath, A. & Arratia, P.E. 2016 Active colloids in complex fluids. Curr. Opin. Colloid Interface Sci. 21, 86–96.CrossRefGoogle Scholar
Phan-Thien, N. & Dou, H.-S. 1999 Viscoelastic flow past a cylinder: drag coefficient. Comput. Meth. Appl. Mech. Engng 180 (3–4), 243–266.CrossRefGoogle Scholar
Purnode, B & Crochet, M.J. 1998 Polymer solution characterization with the FENE-P model. J. Non-Newtonian Fluid Mech. 77 (1–2), 1–20.CrossRefGoogle Scholar
Qu, Z. & Breuer, K.S. 2020 Effects of shear-thinning viscosity and viscoelastic stresses on flagellated bacteria motility. Phys. Rev. Fluids 5, 073103.CrossRefGoogle Scholar
Riley, E.E. & Lauga, E. 2014 Enhanced active swimming in viscoelastic fluids. Europhys. Lett. 108, 34003.CrossRefGoogle Scholar
Shen, X.N. & Arratia, P. 2011 Undulatory swimming in viscoelastic fluids. Phys. Rev. Lett. 106, 208101.CrossRefGoogle ScholarPubMed
Spagnolie, S.E., Liu, B. & Powers, T.R. 2013 Locomotion of helical bodies in viscoelastic fluids: enhanced swimming at large helical amplitudes. Phys. Rev. Lett. 111, 068101.CrossRefGoogle ScholarPubMed
Stewart, P.A., Lay, N., Sussman, M. & Ohta, M. 2008 An improved sharp interface method for viscoelastic and viscous two-phase flows. J. Sci. Comput. 35 (1), 43–61.CrossRefGoogle Scholar
Suarez, S.S. & Pacey, A.A. 2006 Sperm transport in the female reproductive tract. Hum. Reprod. 12, 23–37.Google ScholarPubMed
Sussman, M., Almgren, A.S., Bell, J.B., Colella, P., Howell, L.H. & Welcome, M.L. 1999 An adaptive level set approach for incompressible two-phase flows. J. Comput. Phys. 148 (1), 81–124.CrossRefGoogle Scholar
Teran, J., Fauci, L. & Shelley, M. 2010 Viscoelastic fluid response can increase the speed and efficiency of a free swimmer. Phys. Rev. Lett. 104, 038101.CrossRefGoogle ScholarPubMed
Thielicke, W. & Stamhuis, E.J. 2014 Towards user-friendly, affordable and accurate digital particle image velocimetry in matlab. J. Open Res. Softw. 2, e30.CrossRefGoogle Scholar
Thomases, B. & Guy, R.D. 2014 Mechanisms of elastic enhancement and hindrance for finite-length undulatory swimmers in viscoelastic fluids. Phys. Rev. Lett. 113, 098102.CrossRefGoogle ScholarPubMed
Vahab, M., Sussman, M. & Shoele, K. 2021 Fluid-structure interaction of thin flexible bodies in multi-material multi-phase systems. J. Comput. Phys. 429, 110008.CrossRefGoogle Scholar
Wu, S. & Mohammadigoushki, H. 2018 Sphere sedimentation in wormlike micelles: effect of micellar relaxation spectrum and gradients in micellar extensions. J. Rheol. 62 (5), 1061–1069.CrossRefGoogle Scholar
Wu, S. & Mohammadigoushki, H. 2019 Flow of a model shear-thickening micellar fluid past a falling sphere. Phys. Rev. Fluids 4, 073303.CrossRefGoogle Scholar
Zottl, A. & Yeomans, J.M. 2019 Enhanced bacterial swimming speeds in macromolecular polymer solutions. Nat. Phys. 15, 554–558.CrossRefGoogle Scholar

Wu et al. Supplementary Movie 1

See Figures Supplementary Material

Download Wu et al. Supplementary Movie 1(Video)
Video 10.2 MB

Wu et al. Supplementary Movie 2

See Figures Supplementary Material

Download Wu et al. Supplementary Movie 2(Video)
Video 11.9 MB

Wu et al. Supplementary Movie 3

See Figures Supplementary Material

Download Wu et al. Supplementary Movie 3(Video)
Video 10.2 MB

Wu et al. Supplementary Movie 4

See Figures Supplementary Material

Download Wu et al. Supplementary Movie 4(Video)
Video 9.4 MB

Wu et al. Supplementary Movie 5

See Figures Supplementary Material

Download Wu et al. Supplementary Movie 5(Video)
Video 10 MB

Wu et al. Supplementary Movie 6

See Figures Supplementary Material

Download Wu et al. Supplementary Movie 6(Video)
Video 9.8 MB
Supplementary material: PDF

Wu et al. Figures Supplementary Material

Figures Supplementary Material

Download Wu et al. Figures Supplementary Material(PDF)
PDF 27.8 KB