Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Takatori, Sho C.
and
Brady, John F.
2016.
Forces, stresses and the (thermo?) dynamics of active matter.
Current Opinion in Colloid & Interface Science,
Vol. 21,
Issue. ,
p.
24.
Mallory, S. A.
and
Cacciuto, A.
2016.
Activity-assisted self-assembly of colloidal particles.
Physical Review E,
Vol. 94,
Issue. 2,
Nikola, Nikolai
Solon, Alexandre P.
Kafri, Yariv
Kardar, Mehran
Tailleur, Julien
and
Voituriez, Raphaël
2016.
Active Particles with Soft and Curved Walls: Equation of State, Ratchets, and Instabilities.
Physical Review Letters,
Vol. 117,
Issue. 9,
Speck, Thomas
and
Jack, Robert L.
2016.
Ideal bulk pressure of active Brownian particles.
Physical Review E,
Vol. 93,
Issue. 6,
Burkholder, Eric W.
and
Brady, John F.
2017.
Tracer diffusion in active suspensions.
Physical Review E,
Vol. 95,
Issue. 5,
Hoell, Christian
Löwen, Hartmut
and
Menzel, Andreas M
2017.
Dynamical density functional theory for circle swimmers.
New Journal of Physics,
Vol. 19,
Issue. 12,
p.
125004.
Rodenburg, Jeroen
Dijkstra, Marjolein
and
van Roij, René
2017.
Van't Hoff's law for active suspensions: the role of the solvent chemical potential.
Soft Matter,
Vol. 13,
Issue. 47,
p.
8957.
Theillard, Maxime
Alonso-Matilla, Roberto
and
Saintillan, David
2017.
Geometric control of active collective motion.
Soft Matter,
Vol. 13,
Issue. 2,
p.
363.
Bianchi, Silvio
Saglimbeni, Filippo
and
Di Leonardo, Roberto
2017.
Holographic Imaging Reveals the Mechanism of Wall Entrapment in Swimming Bacteria.
Physical Review X,
Vol. 7,
Issue. 1,
Junot, G.
Briand, G.
Ledesma-Alonso, R.
and
Dauchot, O.
2017.
Active versus Passive Hard Disks against a Membrane: Mechanical Pressure and Instability.
Physical Review Letters,
Vol. 119,
Issue. 2,
Liluashvili, Alexander
Ónody, Jonathan
and
Voigtmann, Thomas
2017.
Mode-coupling theory for active Brownian particles.
Physical Review E,
Vol. 96,
Issue. 6,
Wagner, Caleb G
Hagan, Michael F
and
Baskaran, Aparna
2017.
Steady-state distributions of ideal active Brownian particles under confinement and forcing.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2017,
Issue. 4,
p.
043203.
Takatori, S. C.
and
Brady, J. F.
2017.
Inertial effects on the stress generation of active fluids.
Physical Review Fluids,
Vol. 2,
Issue. 9,
Takatori, S. C.
and
Brady, J. F.
2017.
Superfluid Behavior of Active Suspensions from Diffusive Stretching.
Physical Review Letters,
Vol. 118,
Issue. 1,
Razin, Nitzan
Voituriez, Raphael
Elgeti, Jens
and
Gov, Nir S.
2017.
Forces in inhomogeneous open active-particle systems.
Physical Review E,
Vol. 96,
Issue. 5,
Razin, Nitzan
Voituriez, Raphael
Elgeti, Jens
and
Gov, Nir S.
2017.
Generalized Archimedes' principle in active fluids.
Physical Review E,
Vol. 96,
Issue. 3,
Sokolov, Andrey
Rubio, Leonardo Dominguez
Brady, John F.
and
Aranson, Igor S.
2018.
Instability of expanding bacterial droplets.
Nature Communications,
Vol. 9,
Issue. 1,
Yan, Wen
and
Brady, John F.
2018.
The curved kinetic boundary layer of active matter.
Soft Matter,
Vol. 14,
Issue. 2,
p.
279.
Ostapenko, Tanya
Schwarzendahl, Fabian Jan
Böddeker, Thomas J.
Kreis, Christian Titus
Cammann, Jan
Mazza, Marco G.
and
Bäumchen, Oliver
2018.
Curvature-Guided Motility of Microalgae in Geometric Confinement.
Physical Review Letters,
Vol. 120,
Issue. 6,
Fily, Y
Kafri, Y
Solon, A P
Tailleur, J
and
Turner, A
2018.
Mechanical pressure and momentum conservation in dry active matter.
Journal of Physics A: Mathematical and Theoretical,
Vol. 51,
Issue. 4,
p.
044003.
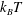 $k_{B}T$ to the swimmer’s activity
$k_{B}T$ to the swimmer’s activity 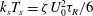 $k_{s}T_{s}={\it\zeta}U_{0}^{2}{\it\tau}_{R}/6$, where
$k_{s}T_{s}={\it\zeta}U_{0}^{2}{\it\tau}_{R}/6$, where 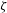 ${\it\zeta}$ is the Stokes drag coefficient,
${\it\zeta}$ is the Stokes drag coefficient, 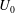 $U_{0}$ is the swim speed and
$U_{0}$ is the swim speed and 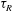 ${\it\tau}_{R}$ is the reorientation time of the active particles. The theory, which is valid on all length and time scales, has a natural microscopic length scale over which concentration and orientation distributions are confined near boundaries, but the microscopic length does not appear in the force. The swim pressure emerges naturally and dominates the behaviour when the boundary size is large compared to the swimmer’s run length
${\it\tau}_{R}$ is the reorientation time of the active particles. The theory, which is valid on all length and time scales, has a natural microscopic length scale over which concentration and orientation distributions are confined near boundaries, but the microscopic length does not appear in the force. The swim pressure emerges naturally and dominates the behaviour when the boundary size is large compared to the swimmer’s run length 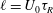 $\ell =U_{0}{\it\tau}_{R}$. The theory is used to predict the motion of bodies of all sizes immersed in active matter.
$\ell =U_{0}{\it\tau}_{R}$. The theory is used to predict the motion of bodies of all sizes immersed in active matter.