No CrossRef data available.
Published online by Cambridge University Press: 11 April 2024
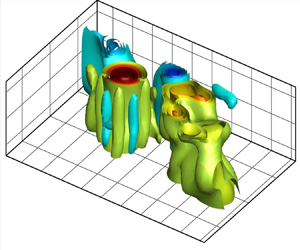
This experimental study investigates the fluid–structure–surface interactions of a flexibly mounted rigid plate in axial flow, focusing on flow-induced vibration (FIV) response and vortex dynamics of the system within a reduced velocity range of  $U^*=0.29\unicode{x2013}8.73$, corresponding to a Reynolds number range of
$U^*=0.29\unicode{x2013}8.73$, corresponding to a Reynolds number range of  $Re=518\unicode{x2013}15\,331$. The plate, with one and two degrees of freedom (DoFs) for pitching and plunging oscillations, is examined at various submerged heights near the free surface. Results show that the plate exhibits divergence instability at low reduced velocities in both 1DoF and 2DoF systems. As the flow velocity surpasses a critical reduced velocity, periodic limit-cycle oscillations (LCOs) occur, increasing in amplitude until a second critical reduced velocity is reached. Beyond this point, LCOs are suppressed, and the plate experiences an increased static divergence angle with further flow velocity increase. The proximity to the free surface significantly influences the FIV response, with decreasing submerged heights leading to reduced LCO amplitudes and a shift of instabilities to higher reduced velocities. Vortex dynamics are analysed using time-resolved volumetric particle tracking velocimetry and hydrogen bubble flow visualisation. The analysis reveals disruptions in the symmetric flow field near the free surface, causing elongation and fragmentation of vortices in the wake of the plate, as well as vortex coupling. Proper orthogonal decomposition (POD) identifies dominant coherent structures, including leading-edge and trailing-edge vortices, captured in the first and second paired modes. On the other hand, higher POD modes capture the interaction of vortices in the wake and near the free surface.
$Re=518\unicode{x2013}15\,331$. The plate, with one and two degrees of freedom (DoFs) for pitching and plunging oscillations, is examined at various submerged heights near the free surface. Results show that the plate exhibits divergence instability at low reduced velocities in both 1DoF and 2DoF systems. As the flow velocity surpasses a critical reduced velocity, periodic limit-cycle oscillations (LCOs) occur, increasing in amplitude until a second critical reduced velocity is reached. Beyond this point, LCOs are suppressed, and the plate experiences an increased static divergence angle with further flow velocity increase. The proximity to the free surface significantly influences the FIV response, with decreasing submerged heights leading to reduced LCO amplitudes and a shift of instabilities to higher reduced velocities. Vortex dynamics are analysed using time-resolved volumetric particle tracking velocimetry and hydrogen bubble flow visualisation. The analysis reveals disruptions in the symmetric flow field near the free surface, causing elongation and fragmentation of vortices in the wake of the plate, as well as vortex coupling. Proper orthogonal decomposition (POD) identifies dominant coherent structures, including leading-edge and trailing-edge vortices, captured in the first and second paired modes. On the other hand, higher POD modes capture the interaction of vortices in the wake and near the free surface.