Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T13:18:55.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid–structure coupling mechanism and its aerodynamic effect on membrane aerofoils

Published online by Cambridge University Press:  13 June 2018

Sonia Serrano-Galiano Open the ORCID record for Sonia Serrano-Galiano [Opens in a new window] ,
Neil D. Sandham Open the ORCID record for Neil D. Sandham [Opens in a new window]  and
Richard D. Sandberg
Sonia Serrano-Galiano*
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Neil D. Sandham
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Richard D. Sandberg
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

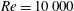Fluid–structure interactions of elastic membrane aerofoils are investigated at Reynolds number $Re=10\,000$ and low angle of attack. The dynamics of the fluid and membrane coupled system are solved using direct numerical simulation (DNS), where the geometry and boundary conditions were applied using a boundary data immersion method. Although membrane aerofoils improve the aerodynamic performance close to stall conditions compared to rigid aerofoils, it has previously been found that membrane aerofoils show lower aerodynamic efficiency at low angles of attack. This study focuses on the coupling mechanism at an angle of attack of 8 degrees, which is below the stall angle. The dynamic behaviour of the coupled system was characterised via spectral analysis in the wavenumber and frequency domain, which allowed the propagating wave nature of the membrane vibrations and their effect on the surrounding pressure field to be clarified. The membrane vibrations are found to introduce upstream-propagating pressure waves that appear to be responsible for a loss in aerodynamic efficiency compared to a rigid aerofoil. Comparison of two- and three-dimensional results reveals that the three-dimensional flow development causes a decrease in the amplitude of the system fluctuations, but the same coupling mechanism is present.

JFM classification

Aerodynamics: Aerodynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 1127 - 1156
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbós-Torrent, S., Ganapathisubramani, B. & Palacios, R. 2013 Leading- and trailing-edge effects on the aeromechanics of membrane aerofoils. J. Fluids Struct. 38, 107–126.CrossRefGoogle Scholar
Bleischwitz, R., de Kat, R. & Ganapathisubramani, B. 2015 Aspect-ratio effects on aeromechanics of membrane wings at moderate Reynolds numbers. AIAA J. 53 (3), 780–788.CrossRefGoogle Scholar
Bleischwitz, R., de Kat, R. & Ganapathisubramani, B. 2016 Aeromechanics of membrane and rigid wings in and out of ground-effect at moderate Reynolds numbers. J. Fluids Struct. 62, 318–331.CrossRefGoogle Scholar
Bleischwitz, R., de Kat, R. & Ganapathisubramani, B. 2017 On the fluid–structure interaction of flexible membrane wings for MAVs in and out of ground-effect. J. Fluids Struct. 70, 214–234.CrossRefGoogle Scholar
Bremner, P. G. & Wilby, J. F. 2002 Aero-vibro-acoustics: problem statement and methods for simulation-based design solution. In 8th AIAA/CEAS Aeroacoustics Conference, American Institute of Aeronautics and Astronautics.Google Scholar
Carrier, G. F. 1945 On the nonlinear vibration problem of the elastic string. Q. Appl. Maths 3, 157–165.CrossRefGoogle Scholar
Dubief, Y. & Delcayre, F. 2000 On coherent-vortex identification in turbulence. J. Turbul. 1, N11.CrossRefGoogle Scholar
Galvao, R., Israeli, E., Song, A., Tian, X., Bishop, K., Swartz, S. & Breuer, K. 2006 the aerodynamics of compliant membrane wings modeled on mammalian flight mechanics. In 36th AIAA Fluid Dynamics Conference and Exhibit, Fluid Dynamics and Co-located Conferences, American Institute of Aeronautics and Astronautics.Google Scholar
Gordnier, R. E. 2009 High fidelity computational simulation of a membrane wing airfoil. J. Fluids Struct. 25 (5), 897–917.CrossRefGoogle Scholar
Gordnier, R. E. & Attar, P. J. 2009 Implicit LES simulations of a low Reynolds number flexible membrane wing airfoil. In 47th AIAA Aerospace Sciences Meeting, vol. 579, American Institute of Aeronautics and Astronautics.Google Scholar
Gordnier, R. E. & Attar, P. J. 2014 Impact of flexibility on the aerodynamics of an aspect ratio two membrane wing. J. Fluids Struct. 45, 138–152.CrossRefGoogle Scholar
Graff, K. F. 1975 Wave Motion in Elastic Solids. Courier.Google Scholar
Horton, H. P.1968 Laminar separation bubbles in two and three dimensional incompressible flow. PhD thesis, Queen Mary University of London.Google Scholar
Hu, H., Tamai, M. & Murphy, J. T. 2008 Flexible-membrane airfoils at low Reynolds numbers. J. Aircraft 45 (5), 1767–1778.CrossRefGoogle Scholar
Ifju, P. G., Jenkins, D. A., Ettinger, S., Lian, Y., Shyy, W. & Waszak, M. R.2002 Flexible-wing-based micro air vehicles. AIAA Paper 2002-0705.CrossRefGoogle Scholar
Jaworski, J. W. & Gordnier, R. E. 2012 High-order simulations of low Reynolds number membrane airfoils under prescribed motion. J. Fluids Struct. 31, 49–66.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2008 Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J. Fluid Mech. 602, 175–207.CrossRefGoogle Scholar
Lian, Y., Shyy, W., Ifju, P. & Verron, E. 2002 A computational model for coupled membrane-fluid dynamics. In 32nd AIAA Fluid Dynamics Conference and Exhibit, Fluid Dynamics and Co-located Conferences, American Institute of Aeronautics and Astronautics. AIAA Paper 2002-2972.Google Scholar
Rojratsirikul, P., Genc, M. S., Wang, Z. & Gursul, I. 2011 Flow-induced vibrations of low aspect ratio rectangular membrane wings. J. Fluids Struct. 27 (8), 1296–1309.CrossRefGoogle Scholar
Rojratsirikul, P., Wang, Z. & Gursul, I. 2009 Unsteady fluid structure interactions of membrane airfoils at low Reynolds numbers. Exp. Fluids 46 (5), 859–872.CrossRefGoogle Scholar
Rojratsirikul, P., Wang, Z. & Gursul, I. 2010 Effect of pre-strain and excess length on unsteady fluid structure interactions of membrane airfoils. J. Fluids Struct. 26 (3), 359–376.CrossRefGoogle Scholar
Sandberg, R. D. 2015 Compressible-flow DNS with application to airfoil noise. Flow Turbul. Combust. 95 (2–3), 211–229.CrossRefGoogle Scholar
Sandberg, R. D. & Sandham, N. D. 2006 Nonreflecting zonal characteristic boundary condition for direct numerical simulation of aerodynamic sound. AIAA J. 44 (2), 402–405.CrossRefGoogle Scholar
Schlanderer, S. C. & Sandberg, R. D. 2014 DNS of an airfoil at angle of attack with an elastic trailing-edge extension. In 19th Australasian Fluid Mechanics Conference.Google Scholar
Schlanderer, S. C., Weymouth, G. D. & Sandberg, R. D. 2017 The boundary data immersion method for compressible flows with application to aeroacoustics. J. Comput. Phys. 333, 440–461.CrossRefGoogle Scholar
Serrano-Galiano, S.2016 Fluid–structure interaction of membrane aerofoils at low Reynolds numbers. PhD thesis, University of Southampton.Google Scholar
Serrano-Galiano, S. & Sandberg, R. D. 2015 Direct numerical simulations of membrane wings at low Reynolds number. In 53rd AIAA Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics. AIAA Paper 2015-1300.Google Scholar
Serrano-Galiano, S. & Sandberg, R. D. 2016 Effect of the leading and trailing edge geometry on the fluid–structural coupling of membrane aerofoils. In 54th AIAA Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics. AIAA Paper 2016-0853.Google Scholar
Shen, L., Zhang, X., Yue, D. K. P. & Triantafyllou, M. S. 2003 Turbulent flow over a flexible wall undergoing a streamwise travelling wave motion. J. Fluid Mech. 484, 197–221.CrossRefGoogle Scholar
Shyy, W., Ifju, P. & Viieru, D. 2005 Membrane wing-based micro air vehicles. Appl. Mech. Rev. 58 (4), 283.CrossRefGoogle Scholar
Smith, R. & Shyy, W. 1997 Incremental potential flow based membrane wing element. AIAA J. 35.CrossRefGoogle Scholar
Waszak, M. R., Jenkins, L. N. & Ifju, P. G. 2001 Stability and control properties of an aeroelastic fixed wing micro aerial vehicle. AIAA Paper 2001-4005.Google Scholar
Weymouth, G. D. & Yue, D. K. P. 2011 Boundary data immersion method for Cartesian-grid simulations of fluid–body interaction problems. J. Comput. Phys. 230 (16), 6233–6247.CrossRefGoogle Scholar
White, F. M. 1991 Viscous Fluid Flow. McGraw-Hill.Google Scholar