Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T08:46:35.787Z Has data issue: false hasContentIssue false
  • English
  • Français

A fluid-mechanical model of elastocapillary coalescence

Published online by Cambridge University Press:  25 March 2014

Kiran Singh ,
John R. Lister  and
Dominic Vella
Kiran Singh
Affiliation:
OCCAM, Mathematical Institute, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK
John R. Lister
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Dominic Vella*
Affiliation:
OCCAM, Mathematical Institute, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

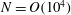We present a fluid-mechanical model of the coalescence of a number of elastic objects due to surface tension. We consider an array of spring–block elements separated by thin liquid films, whose dynamics are modelled using lubrication theory. With this simplified model of elastocapillary coalescence, we present the results of numerical simulations for a large number of elements, $N=O(10^4)$. A linear stability analysis shows that pairwise coalescence is always the most unstable mode of deformation. However, the numerical simulations show that the cluster sizes actually produced by coalescence from a small white-noise perturbation have a distribution that depends on the relative strength of surface tension and elasticity, as measured by an elastocapillary number 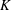$K$. Both the maximum cluster size and the mean cluster size scale like 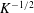$K^{-1/2}$ for small 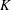$K$. An analytical solution for the response of the system to a localized perturbation shows that such perturbations generate propagating disturbance fronts, which leave behind ‘frozen-in’ clusters of a predictable size that also depends on 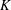$K$. A good quantitative comparison between the cluster-size statistics from noisy perturbations and this ‘frozen-in’ cluster size suggests that propagating fronts may play a crucial role in the dynamics of coalescence.

JFM classification

Interfacial Flows (free surface): Capillary flows Low-Reynolds-number flows: Lubrication theory Micro-/Nano-fluid dynamics: MEMS/NEMS
Type
Papers
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , pp. 621 - 646
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aristoff, J. M., Duprat, C. & Stone, H. A. 2011 Elastocapillary imbibition. Intl J. Non-Linear Mech. 46, 648–656.CrossRefGoogle Scholar
Bender, C. M. & Orszag, S. A. 1991 Advanced Mathematical Methods for Scientists and Engineers. Springer.Google Scholar
Bico, J., Roman, B., Moulin, L. & Boudaoud, A. 2004 Adhesion: elastocapillary coalescence in wet hair. Nature 432, 690.Google Scholar
Boudaoud, A., Bico, J. & Roman, B. 2007 Elastocapillary coalescence: aggregation and fragmentation with a maximal size. Phys. Rev. E 76, 060102.Google Scholar
Bush, J. W. M. & Hu, D. L. 2006 Walking on water: biolocomotion at the interface. Annu. Rev. Fluid Mech. 38, 339–369.Google Scholar
Bush, J. W. M., Hu, D. L. & Prakash, M. 2008 The integument of water-walking arthropods: form and function. Adv. Insect Physiol. 34, 117–192.CrossRefGoogle Scholar
Cambau, T., Bico, J. & Reyssat, E. 2011 Capillary rise between flexible walls. Europhys. Lett. 96, 24001.CrossRefGoogle Scholar
Chakrapani, N., Wei, B., Carrillo, A., Ajayan, P. M. & Kane, R. S. 2004 Capillarity-driven assembly of two-dimensional cellular carbon nanotube foams. Proc. Natl Acad. Sci. USA 101, 4009–4012.CrossRefGoogle ScholarPubMed
Chiodi, F., Roman, B. & Bico, J. 2010 Piercing an interface with a brush: collaborative stiffening. Europhys. Lett. 90, 44006.Google Scholar
de Langre, E., Baroud, C. N. & Reverdy, P. 2009 Energy criteria for elasto-capillary wrapping. J. Fluids Struct. 26, 205–217.CrossRefGoogle Scholar
de Volder, M. F. L. & Hart, A. J. 2013 Engineering hierarchical nanostructures by elastocapillary self-assembly. Angew. Chem. Intl Ed. 52, 2412–2425.Google Scholar
de Volder, M. F. L., Park, S. J., Tawfick, S. H., Vidaud, D. O. & Hart, A. J. 2011 Fabrication and electrical integration of robust carbon nanotube micropillars by self-directed elastocapillary densification. J. Micromech. Microengng 21, 045033.Google Scholar
Duprat, C., Aristoff, J. M. & Stone, H. A. 2011 Dynamics of elastocapillary rise. J. Fluid Mech. 679, 641–654.CrossRefGoogle Scholar
Duprat, C., Protiére, S., Beebe, A. & Stone, H. 2012 Wetting of flexible fibre arrays. Nature 482, 510–513.Google Scholar
Fermigier, M., Limat, L., Wesfreid, J. E., Boudinet, P. & Quilliet, C. 1992 Two-dimensional patterns in the Rayleigh–Taylor instability of thin films. J. Fluid Mech. 236, 349–383.CrossRefGoogle Scholar
Gat, A. D. & Gharib, M. 2013 Elasto-capillary coalescence of multiple parallel sheets. J. Fluid Mech. 723, 692–705.CrossRefGoogle Scholar
Goldstein, R. E., Nelson, P., Powers, T. & Seifert, U. 1996 Front propagation in the pearling instability of tubular vesicles. J. Phys. II France 6, 767–796.Google Scholar
Hinch, E. J. 1990 Perturbation Methods. Cambridge University Press.Google Scholar
Huang, J., Juszkiewicz, M., de Jeu, W. H., Cerda, E., Emrick, T., Menon, N. & Russell, T. P. 2007 Capillary wrinkling of floating thin polymer films. Science 317, 650–653.Google Scholar
Jung, S., Reis, P. M., James, J., Clanet, C. & Bush, J. W. M. 2009 Capillary origami in nature. Phys. Fluids 21, 091110.Google Scholar
Kim, H. -Y. & Mahadevan, L. 2006 Capillary rise between elastic sheets. J. Fluid Mech. 548, 141–150.Google Scholar
Limat, L., Jenffer, P., Dagens, B., Touron, E., Fermigier, M. & Wesfreid, J. E. 1992 Gravitational instabilities of thin liquid layers: dynamics of pattern selection. Physica D 61, 166–182.Google Scholar
Lister, J. R., Rallison, J. M. & Rees, S. J. 2010 The nonlinear dynamics of pendant drops on a thin film coating the underside of a ceiling. J. Fluid Mech. 647, 239–264.Google Scholar
Mastrangelo, C. H. & Hsu, C. H. 1993 Mechanical stability and adhesion of microstructures under capillary forces—part 1: basic theory. J. Microelectromech. Syst. 2, 33–43.Google Scholar
Neukirch, S., Roman, B., Gaudemaris, B. & Bico, B. 2007 Elasto-capillary interactions: piercing an interface with an elastic rod. J. Mech. Phys. Solids 55, 1212–1235.Google Scholar
O’Hara, P. D. & Morandin, L. A. 2010 Effects of sheens associated with offshore oil and gas development on the feather microstructure of pelagic seabirds. Mar. Pollut. Bull. 60, 672–678.Google Scholar
Pokroy, B., Kang, S. H., Mahadevan, L. & Aizenberg, J. 2009 Self-organisation of a mesoscale bristle into ordered hierarchical helical assemblies. Science 323, 237–240.Google Scholar
Powers, T. R. & Goldstein, R. E. 1997 Pearling and pinchining: propagation of Rayleigh instabilities. Phys. Rev. Lett. 78, 2555–2558.Google Scholar
Py, C., Bastien, R., Bico, J., Roman, B. & Boudaoud, A. 2007a 3D aggregation of wet fibres. Europhys. Lett. 77, 44005.Google Scholar
Py, C., Reverdy, P., Doppler, L., Bico, J., Roman, B. & Baroud, C. 2007b Capillary origami: spontaneous wrapping of a droplet with an elastic sheet. Phys. Rev. Lett. 98, 156103.Google Scholar
Schroll, R. D., Adda-Bedia, M., Cerda, E., Huang, J., Menon, N., Russell, T. P., Toga, K. B., Vella, D. & Davidovitch, B. 2013 Capillary deformations of bendable films. Phys. Rev. Lett. 111, 014301.Google Scholar
Song, Y. S. & Sitti, M. 2007 Surface-tension-driven biologically inspired water strider robots: theory and experiments. IEEE Trans. Robot. 23, 578–589.Google Scholar
Tanaka, T., Morigami, M. & Atoda, N. 1993 Mechanism of resist pattern collapse during development process. Japan. J. Appl. Phys. 32, 6059–6064.Google Scholar
Taroni, M. & Vella, D. 2012 Multiple equilibria in a simple elastocapillary system. J. Fluid Mech. 712, 273–294.Google Scholar
Timoshenko, S. P. & Goodier, J. N. 1970 Theory of Elasticity. McGraw-Hill.Google Scholar
van Saarloos, W. 2003 Front propagation into unstable states. Phys. Rep. 286, 29–222.CrossRefGoogle Scholar
Vella, D. 2008 Floating objects with finite resistance to bending. Langmuir 24, 8701–8706.Google Scholar
Vella, D., Adda-Bedia, M. & Cerda, E. 2010 Capillary wrinkling of elastic membranes. Soft Matt. 6, 5782.Google Scholar