Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T13:17:59.745Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid transport in geological reservoirs with background flow

Published online by Cambridge University Press:  24 August 2017

Samuel S. Pegler Open the ORCID record for Samuel S. Pegler [Opens in a new window] ,
Alexandra S. D. Maskell ,
Katherine A. Daniels  and
Mike J. Bickle
Samuel S. Pegler*
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
Alexandra S. D. Maskell
Affiliation:
Department of Earth Sciences, University of Cambridge, Cambridge CB2 3EQ, UK
Katherine A. Daniels
Affiliation:
Department of Earth Sciences, University of Cambridge, Cambridge CB2 3EQ, UK British Geological Survey, Keyworth, NG12 599, UK
Mike J. Bickle
Affiliation:
Department of Earth Sciences, University of Cambridge, Cambridge CB2 3EQ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents fundamental analysis of the injection and release of fluid into porous media or geological reservoirs saturated by a different fluid undergoing a background flow, and tests the predictions using analogue laboratory experiments. The study reveals new results important for an understanding of the transport of hazardous contaminants through aquifers and the long-term fate of carbon dioxide (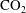$\text{CO}_{2}$) in geological 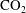$\text{CO}_{2}$ sequestration. Using numerical and asymptotic analysis, we describe a variety of flow regimes that arise, and demonstrate an almost instantaneous control of injected fluid by the far field conditions in geological reservoirs. For a continuous input, the flow develops a horizontal interface between the injected and ambient fluids. The background flow thereby effectively caps the height of the injected fluid into a shallower region of vertical confinement. For a released parcel of fluid, gravitational spreading is found to become negligible after a short time. A dominant control of the interface by the background pressure gradient arises, and stems from the different velocities at which it drives the injected and ambient fluids individually. Similarity solutions describing these dynamics show that the parcel approaches a slender triangular profile that grows horizontally as 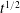$t^{1/2}$, where $t$ is time, a rate faster than relaxation under gravity. Shock layers develop at the front or back of the parcel, depending on whether it is more or less viscous than the ambient fluid. New analytical results describing the long-term effects of residual trapping due to capillary retention are developed, which yield explicit predictions for the time and length scales on which a parcel of $\text{CO}_{2}$ becomes retained. We end by applying our results to geological contexts, concluding that even slight background motion can have considerable implications for long-term transport through the subsurface.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 827 , 25 September 2017 , pp. 536 - 571
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allis, R., White, S., Chidsey, T., Gwynn, W., Morgan, C., Adams, M. & Moore, J. 2001 Natural CO2 reservoirs on the Colorado Plateau and Southern Rocky Mountains: candidates for CO2 sequestration. In Proceedings of the First National Conference on Carbon Sequestration, Washington DC, May 2001.Google Scholar
Barenblatt, G. I. 1952 On some unsteady motions of fluids and gases in a porous medium. Prikl. Mat. Mekh. 16, 67–78.Google Scholar
Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Bickle, M. J. 2009 Geological carbon storage. Nat. Geosci. 2, 815–818.CrossRefGoogle Scholar
Boait, F. C., White, N. J., Bickle, M. J., Chadwick, R. A., Neufeld, J. A. & Huppert, H. E. 2012 Spatial and temporal evolution of injected CO2 at the Sleipner Field, North Sea. J. Geophys. Res. 117, B03309.Google Scholar
Dubacq, B., Bickle, M. J. & Evans, K. 2013 An activity model for phase equilibria in the H2O–CO2 –NaCl system. Geochim. Cosmochim. Acta 110, 229–252.Google Scholar
Golding, M. J. & Huppert, H. E. 2010 The effect of confining impermeable boundaries on gravity currents in a porous medium. J. Fluid Mech. 649, 1–17.Google Scholar
Gunn, I. & Woods, A. W. 2011 On the flow of buoyant fluid injected into a confined, inclined aquifer. J. Fluid Mech. 672, 109–129.Google Scholar
Gunn, I. & Woods, A. W. 2012 On the flow of buoyant fluid injected into an aquifer with a background flow. J. Fluid Mech. 706, 274–294.Google Scholar
Guo, B., Zheng, Z., Celia, M. A. & Stone, H. A. 2016 Axisymmetric flows from fluid injection into a confined porous medium. Phys. Fluids 28, 022107.Google Scholar
Hesse, M. A., Orr, F. M. & Tchelepi, H. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.Google Scholar
Hesse, M. A., Tchelepi, H. A., Cantwell, B. J. & Orr, F. M. 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363–383.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Kampman, N., Bickle, M., Becker, J., Assayag, N. & Chapman, H. 2009 Feldspar dissolution kinetics and Gibbs free energy dependence in a CO2 -enriched groundwater system, Green River, Utah. Earth Planet. Sci. Lett. 284, 473–488.Google Scholar
Kampman, N., Bickle, M. J., Maskell, A., Chapman, H. J., Evans, J. P., Purser, G., Zhou, Z., Schaller, M. F., Gattacceca, J. C., Bertier, P. et al. 2014 Drilling and sampling a natural CO2 reservoir: implications for fluid flow and CO2 –fluid–rock reactions during CO2 migration through the overburden. Chem. Geol. 369, 51–82.Google Scholar
de Loubens, R. & Ramakrishnan, T. S. 2011a Analysis and computation of gravity induced migration in porous media. J. Fluid Mech. 675, 60–86.Google Scholar
de Loubens, R. & Ramakrishnan, T. S. 2011b Asymptotic solution of a nonlinear advection–diffusion equation. Q. Appl. Maths 69, 389–401.CrossRefGoogle Scholar
Lyle, S., Huppert, H. E., Hallworth, M., Bickle, M. & Chadwick, A. 2005 Axisymmetric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.Google Scholar
MacMinn, C. W. & Juanes, R. 2009 Post-injection spreading and trapping of CO2 in saline aquifers: impact of the plume shape at the end of injection. Comput. Geosci. 13, 480–491.Google Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2010 CO2 migration in saline aquifers. Part 1. Capillary trapping under slope and groundwater flow. J. Fluid Mech. 662, 329–351.Google Scholar
Maskell, A. S. D.2017 Migration and interaction of $\text{CO}_{2}$ –brine through caprocks and reservoir rocks: lessons from the naturally leaking Green River $\text{CO}_{2}$ accumulation, Utah. PhD thesis, Univeristy of Cambridge.Google Scholar
Neufeld, J. A., Vella, D. & Huppert, H. E. 2009 The effect of a fissure on storage in a porous medium. J. Fluid Mech. 639, 239–259.CrossRefGoogle Scholar
Nordbotten, J. M. & Celia, M. A. 2006 Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.Google Scholar
Nordbotten, J. M., Celia, M. A. & Bachu, S. 2005 Injection and storage of CO2 in deep saline aquifers: analytical solution for CO2 plume evolution during injection. Trans. Porous Med. 55, 339–360.Google Scholar
Orr, F. M. 2009 Onshore geological storage of CO2 . Science 325, 1656–1658.Google Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2013a Topographic controls on gravity currents in porous media. J. Fluid Mech. 734, 317–337.Google Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2014a Fluid injection into a confined porous layer. J. Fluid Mech. 745, 592–620.Google Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2014b Fluid migration between confined aquifers. J. Fluid Mech. 757, 330–353.CrossRefGoogle Scholar
Pegler, S. S., Kowal, K. N., Hasenclever, L. Q. & Worster, M. G. 2013b Lateral controls on grounding-line dynamics. J. Fluid Mech. 722, R1.Google Scholar
Pritchard, D. 2007 Gravity currents over fractured substrates in a porous medium. J. Fluid Mech. 584, 415–431.Google Scholar
Unwin, H. J. T., Wells, G. N. & Woods, A. W. 2016 CO2 dissolution in a background hydrological flow. J. Fluid Mech. 789, 768–784.Google Scholar
Vella, D. & Huppert, H. E. 2006 Gravity currents in a porous medium at an inclined plane. J. Fluid Mech. 555, 353–362.Google Scholar
Wigley, M., Kampman, N., Dubacq, B. & Bickle, M. 2012 Fluid–mineral reactions and trace metal mobilisation in an exhumed natural CO2 reservoir, Green River, Utah. Geology 40, 555–558.Google Scholar
Zheng, Z., Guo, B., Christov, I. C., Celia, M. A. & Stone, H. A. 2015 Flow regimes for fluid injection into a confined porous medium. J. Fluid Mech. 767, 881–909.Google Scholar

Pegler et al. supplementary movie

Movie of run 4, showing the injection of dyed brine into a porous bead pack containing an ambient background flow of saturating water. The theoretical prediction is shown as a red dashed curve.

Download Pegler et al. supplementary movie(Video)
Video 11.8 MB