Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T06:14:13.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid transport by individual microswimmers

Published online by Cambridge University Press:  30 May 2013

Dmitri O. Pushkin ,
Henry Shum  and
Julia M. Yeomans
Dmitri O. Pushkin*
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, 1 Keble Road, Oxford OX1 3NP, UK
Henry Shum
Affiliation:
Department of Chemical and Petroleum Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA
Julia M. Yeomans
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, 1 Keble Road, Oxford OX1 3NP, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

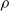We discuss the path of a tracer particle as a microswimmer moves past on an infinite, straight trajectory. If the tracer is sufficiently far from the path of the swimmer it moves in a closed loop. As the initial distance between the tracer and the path of the swimmer $\rho $ decreases, the tracer is displaced a small distance backwards (relative to the direction of the swimmer velocity). For much smaller tracer–swimmer separations, however, the tracer displacement becomes positive and diverges as 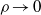$\rho \rightarrow 0$. To quantify this behaviour we calculate the Darwin drift, the total volume swept out by a material sheet of tracers, initially perpendicular to the swimmer path, during the swimmer motion. We find that the drift can be written as the sum of a universal term which depends on the quadrupolar flow field of the swimmer, together with a non-universal contribution given by the sum of the volumes of the swimmer and its wake. The formula is compared to exact results for the squirmer model and to numerical calculations for a more realistic model swimmer.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Low-Reynolds-number flows: Low-Reynolds-number flows Mixing: Mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 726 , 10 July 2013 , pp. 5 - 25
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, T. B. 1986 Note on added mass and drift. J. Fluid Mech. 169, 251–256.CrossRefGoogle Scholar
Berg, H. C. 2004 E. Coli in Motion. Springer.CrossRefGoogle Scholar
Blake, J. R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46, 199–208.CrossRefGoogle Scholar
Chwang, A. T. & Wu, T. Y.-T. 1975 Hydromechanics of low-Reynolds-number flow. Part 2. Singularity method for Stokes flows. J. Fluid Mech. 67, 787–815.CrossRefGoogle Scholar
Darwin, C. 1953 Note on hydrodynamics. Math. Proc. Camb. Phil. Soc. 49 (2), 342–354.CrossRefGoogle Scholar
Dombrowski, C., Cisneros, L., Chatkaew, S., Goldstein, R. E. & Kessler, J. O. 2004 Self-concentration and large-scale coherence in bacterial dynamics. Phys. Rev. Lett. 93 (9), 98103.CrossRefGoogle ScholarPubMed
Drescher, K., Dunkel, J., Cisneros, L. H., Ganguly, S. & Goldstein, R. E. 2011 Fluid dynamics and noise in bacterial cell–cell and cell-surface scattering. Proc. Natl Acad. Sci.CrossRefGoogle ScholarPubMed
Drescher, K., Goldstein, R. E., Michel, N., Polin, M. & Tuval, I. 2010 Direct measurement of the flow field around swimming microorganisms. Phys. Rev. Lett. 105, 168101.CrossRefGoogle ScholarPubMed
Dunkel, J., Putz, V. B., Zaid, I. M. & Yeomans, J. M. 2010 Swimmer-tracer scattering at low Reynolds number. Soft Matt. 6, 4268–4276.CrossRefGoogle Scholar
Eames, I., Belcher, S. E. & Hunt, J. C. R. 1994 Drift, partial drift and Darwin’s proposition. J. Fluid Mech. 275, 201–223.CrossRefGoogle Scholar
Eames, I., Gobby, D. & Dalziel, S. B. 2003 Fluid displacement by Stokes flow past a spherical droplet. J. Fluid Mech. 485, 67–85.CrossRefGoogle Scholar
Guasto, J. S., Johnson, K. A. & Gollub, J. P. 2010 Oscillatory flows induced by microorganisms swimming in two dimensions. Phys. Rev. Lett. 105, 168102.CrossRefGoogle ScholarPubMed
Ishikawa, T., Locsei, J. T. & Pedley, T. J. 2010 Fluid particle diffusion in a semidilute suspension of model micro-organisms. Phys. Rev. E 82, 021408.CrossRefGoogle Scholar
Ishikawa, T., Simmonds, M. P. & Pedley, T. J. 2006 Hydrodynamic interaction of two swimming model micro-organisms. J. Fluid Mech. 568, 119–160.CrossRefGoogle Scholar
Katija, K. & Dabiri, J. O. 2009 A viscosity-enhanced mechanism for biogenic ocean mixing. Nature 460, 624–626.CrossRefGoogle ScholarPubMed
Keller, J. B. & Rubinow, S. I. 1976 Swimming of flagellated microorganisms. Biophys. J. 2, 151–170.CrossRefGoogle Scholar
Kurtuldu, H., Guasto, J. S., Johnson, K. A. & Gollub, J. P. 2011 Enhancement of biomixing by swimming algal cells in two-dimensional films. Proc. Natl Acad. Sci. 108, 10391–10395.CrossRefGoogle ScholarPubMed
Leptos, K. C., Guasto, J. S., Gollub, J. P., Pesci, A. I. & Goldstein, R. E. 2009 Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. Lett. 103, 198103.CrossRefGoogle ScholarPubMed
Leshansky, A. M. & Pismen, L. M. 2010 Do small swimmers mix the ocean? Phys. Rev. E 82, 025301.CrossRefGoogle ScholarPubMed
Lighthill, M. J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5, 109–118.CrossRefGoogle Scholar
Lin, Z., Thiffeault, J.-L. & Childress, S. 2011 Stirring by squirmers. J. Fluid Mech. 669, 167–177.CrossRefGoogle Scholar
Miño, G., Mallouk, T. E., Darnige, T., Hoyos, M., Dauchet, J., Dunstan, J., Soto, R., Wang, Y., Rousselet, A. & Clement, E. 2011 Enhanced diffusion due to active swimmers at a solid surface. Phys. Rev. Lett. 106, 048102.CrossRefGoogle Scholar
Polin, M., Tuval, I., Drescher, K., Gollub, J. P. & Goldstein, R. E. 2009 Chlamydomonas swims with two ‘gears’ in a eukaryotic version of run-and-tumble locomotion. Science 325, 487–490.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Method for Linearized Viscous Flows. Cambridge University Press.CrossRefGoogle Scholar
Purcell, E. M. 1977 Life at low Reynolds number. Am. J. Phys. 45, 3–11.CrossRefGoogle Scholar
Rushkin, I., Kantsler, V. & Goldstein, R. E. 2010 Fluid velocity fluctuations in a suspension of swimming protists. Phys. Rev. Lett. 105, 188101.CrossRefGoogle Scholar
Shum, H., Gaffney, E. A. & Smith, D. J. 2010 Modelling bacterial behaviour close to a no-slip plane boundary: the influence of bacterial geometry. Proc. R. Soc. Lond. A 466, 1725–1748.Google Scholar
Sokolov, A., Goldstein, R. E., Feldchtein, F. I. & Aranson, I. S. 2009 Enhanced mixing and spatial instability in concentrated bacterial suspensions. Phys. Rev. E 80, 031903.CrossRefGoogle ScholarPubMed
Stocker, R. & Durham, W. M. 2009 Tumbling for stealth?. Science 325 (5939), 400–402.CrossRefGoogle ScholarPubMed
Taylor, G. I. 1928 The energy of a body moving in an infinite fluid, with an application to airships. Proc. R. Soc. Lond. A 120 (784), 13–21.Google Scholar
Thiffeault, J.-L. & Childress, S. 2010 Stirring by swimming bodies. Phys. Lett. A 374 (34), 3487–3490.CrossRefGoogle Scholar
Underhill, P. T. & Graham, M. D. 2011 Correlations and fluctuations of stress and velocity in suspensions of swimming microorganisms. Phys. Fluids 23 (12), 121902.CrossRefGoogle Scholar
Underhill, P. T., Hernandez-Ortiz, J. P. & Graham, M. D. 2008 Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 100, 248101.CrossRefGoogle ScholarPubMed
Visser, A. W. 2007 Biomixing of the oceans? Science 316 (5826), 838–839.CrossRefGoogle ScholarPubMed
Wu, X.-L. & Libchaber, A. 2000 Particle diffusion in a quasi-two-dimensional bacterial bath. Phys. Rev. Lett. 84, 3017–3020.CrossRefGoogle Scholar
Zaid, I. M., Dunkel, J. & Yeomans, J. M. 2011 Lévy fluctuations and mixing in dilute suspensions of algae and bacteria. J. R. Soc. Interface 8 (62), 1314–1331.CrossRefGoogle ScholarPubMed