Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T21:45:15.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow-induced vibration control of a circular cylinder using rotational oscillation feedback

Published online by Cambridge University Press:  21 May 2018

D. Vicente-Ludlam ,
A. Barrero-Gil Open the ORCID record for A. Barrero-Gil [Opens in a new window]  and
A. Velazquez
D. Vicente-Ludlam
Affiliation:
Department of Fluid Mechanics and Aerospace Propulsion, Universidad Politecnica de Madrid, Madrid, 28040, Spain
A. Barrero-Gil*
Affiliation:
Department of Fluid Mechanics and Aerospace Propulsion, Universidad Politecnica de Madrid, Madrid, 28040, Spain
A. Velazquez
Affiliation:
Department of Fluid Mechanics and Aerospace Propulsion, Universidad Politecnica de Madrid, Madrid, 28040, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of imposed rotation on a slender elastically mounted circular cylinder free to oscillate transversely to the incident flow has been studied experimentally in a free-surface water channel. Rotation rate and direction are imposed to be proportional to either the cylinder’s transverse displacement or the cylinder’s transverse velocity to determine the effectiveness of these rotation laws to control the dynamics of the cylinder, either to reduce or to enhance oscillations. The former can be of interest for energy harvesting purposes whereas the latter can be useful to avoid unwanted oscillations. 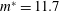In all cases, non-dimensional mass and damping are fixed ($m^{\ast }=11.7$, 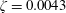$\unicode[STIX]{x1D701}=0.0043$) so the analysis is focused on the role of the rotation law and the reduced velocity. The Reynolds number based on the diameter of the cylinder ranges from 1500 to 10 000. Results are presented in terms of steady-state oscillation characterization (say, amplitude and frequency) and wake-pattern topology, which was obtained through digital particle image velocimetry. Both laws are able to either reduce or enhance oscillations, but they do it in a different way. A rotation law proportional to the cylinder’s displacement is more effective to enhance oscillations. For high enough actuation, a galloping-type response has been found, with a persistent growth of the amplitude of oscillations with the reduced velocity that shows a new desynchronized mode of vortex shedding. On the other hand, a rotation law proportional to the cylinder’s transverse velocity is more efficient to reduce oscillations. In this case only vortex-induced-type responses have been found. A quasi-steady theoretical model has been developed, which helps to explain why a galloping-type response may appear when rotation is proportional to cylinder displacement and is able to predict reasonably the amplitude of oscillations in those cases. The model also explains why a galloping-type response is not expected to occur when rotation is proportional to the cylinder’s velocity.

JFM classification

Aerodynamics: Aerodynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 93 - 118
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdelkefi, A., Hajj, M. R. & Nayfeh, A. H. 2012 Power harvesting from transverse galloping of square cylinder. Nonlinear Dyn. 70 (2), 1355–1363.CrossRefGoogle Scholar
Abdelkefi, A., Hajj, M. R. & Nayfeh, A. H. 2013 Piezoelectric energy harvesting from transverse galloping of bluff bodies. Smart Mater. Struct. 22 (1), 015014.Google Scholar
Al-Mdallal, Q. M.2004 Analysis and computation of the cross-flow past an oscillating cylinder with two degrees of freedom. PhD thesis, Memorial University of Newfoundland.Google Scholar
Assi, G. R. S., Meneghini, J. R., Aranha, J. A. P., Bearman, P. W. & Casaprima, E. 2006 Experimental investigation of flow-induced vibration interference between two circular cylinders. J. Fluids Struct. 22 (6), 819–827.CrossRefGoogle Scholar
Barrero-Gil, A., Sanz-Andres, A. & Alonso, G. 2010 Energy harvesting from transverse galloping. J. Sound Vib. 329 (14), 2873–2883.CrossRefGoogle Scholar
Barrero-Gil, A., Pindado, S. & Avila, S. 2012 Extracting energy from vortex-induced vibrations: a parametric study. Appl. Math. Model. 36 (7), 3153–3160.CrossRefGoogle Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27, 648–658.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.Google Scholar
Bernitsas, M. M., Raghavan, K., Ben-Simon, Y. & Garcia, E. M. H. 2008 VIVACE (Vortex Induced Vibration Aquatic Clean Energy): a new concept in generation of clean and renewable energy from fluid. Trans. ASME J. Offshore Mech. Arctic Engng 130 (4), 041101.Google Scholar
Blackburn, H. M., Elston, J. R. & Sheridan, J. 1999 Bluff body propulsion produced by combined rotary and translational oscillation. Phys. Fluids 11 (1), 4–6.Google Scholar
Blevins, R. 1990 Flow-Induced Vibrations. Van Nostrand Reinhold.Google Scholar
Bourguet, R. & Jacono, D. L. 2014 Flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 740, 342–380.Google Scholar
Bradshaw, P. & Pankhurst, R. C. 1964 The design of low-speed wind tunnels. Prog. Aerosp. Sci. 5, 1–69.CrossRefGoogle Scholar
Doaré, O. & Michelin, S. 2011 Piezoelectric coupling in energy-harvesting fluttering flexible plates: linear stability analysis and conversion efficiency. J. Fluids Struct. 27 (8), 1357–1375.Google Scholar
Fujisawa, N., Kawaji, Y. & Ikemoto, K. 2001 Feedback control of vortex shedding from a circular cylinder by rotational oscillations. J. Fluids Struct. 15, 23–27.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
Govardhan, R. N. & Williamson, C. H. K. 2006 Defining the modified Griffin plot in vortex-induced vibration: revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 561, 147–180.CrossRefGoogle Scholar
Grouthier, C., Michelin, S. & de Langre, E. 2013 Energy harvesting by vortex-induced vibrations in slender structures. In ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, pp. V007T08A013–V007T08A013. American Society of Mechanical Engineers.Google Scholar
Jung, H. J. & Lee, S. W. 2011 The experimental validation of a new energy harvesting system based on the wake galloping phenomenon. Smart Mater. Struct. 20 (5), 055022.CrossRefGoogle Scholar
Karabelas, S. J., Koumroglou, B. C., Argyropoulos, C. D. & Markatos, N. C. 2012 High Reynolds number turbulent flow past a rotating cylinder. Appl. Math. Model. 36 (1), 379–398.CrossRefGoogle Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7), 813–851.Google Scholar
Klamo, J. T.2007 Effects of damping and Reynolds number on vortex-induced vibrations. Doctoral dissertation, California Institute of Technology.Google Scholar
Kocabiyik, S. & Al-Mdallal, Q. M. 2005 Bluff-body flow created by combined rotary and translational oscillation. In Fluid Structure Interaction and Moving Boundary Problems, WIT Transactions on the Built Environment, vol. 84, pp. 195–203. WIT Press.Google Scholar
Lu, L., Qin, J., Teng, B. & Li, Y. 2011 Numerical investigations of lift suppression by feedback rotary oscillation of circular cylinder at low Reynolds number. Phys. Fluids 23, 033601.CrossRefGoogle Scholar
Ma, X., Karniadakis, G. E., Park, H. & Gharib, M. 2003 DPIV-driven flow simulation: a new computational paradigm. Proc. R. Soc. Lond. A 459 (2031), 547–565.CrossRefGoogle Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Morse, T. L., Govardhan, R. N. & Williamson, C. H. K. 2008 The effect of end conditions on the vortex-induced vibration of cylinders. J. Fluids Struct. 24 (8), 1227–1239.Google Scholar
Morse, T. L. & Williamson, C. H. K. 2009 Fluid forcing, wake modes, and transitions for a cylinder undergoing controlled oscillations. J. Fluids Struct. 25 (4), 697–712.CrossRefGoogle Scholar
Naudascher, E. & Rockwell, D. 1994 Flow-Induced Vibrations: An Engineering Guide. A. A. Balkema.Google Scholar
Nazarinia, M., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2009a Flow behind a cylinder forced by a combination of oscillatory translational and rotational motions. Phys. Fluids 21 (5), 051701.Google Scholar
Nazarinia, M., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2009b The three-dimensional wake of a cylinder undergoing a combination of translational and rotational oscillation in a quiescent fluid. Phys. Fluids 21 (6), 064101.Google Scholar
Paidoussis, M. P., Stuart, J. P. & De Langre, E. 2011 Fluid–Structure Interactions. Cambridge University Press.Google Scholar
Parkinson, G. 1989 Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aerosp. Sci. 26 (2), 169–224.Google Scholar
Prasnath, T. K. & Mittal, S. 2008 Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 594, 463–491.CrossRefGoogle Scholar
Sanchez-Sanz, M., Fernandez, B. & Velazquez, A. 2009 Energy-harvesting micro-resonator based on the forces generated by the Karman street around a rectangular prism. J. Microelectromech. Syst. 18, 449–457.CrossRefGoogle Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Sarpkaya, T. 2010 Wave Forces on Offshore Structures. Cambridge University Press.Google Scholar
Seyed-Aghazadeh, B. & Modarres-Sadeghi, Y. 2015 An experimental investigation of vortex-induced vibration of a rotating circular cylinder in the crossflow direction. Phys. Fluids 27 (6), 067101.CrossRefGoogle Scholar
Singh, K., Michelin, S. & De Langre, E. 2012 Energy harvesting from axial fluid-elastic instabilities of a cylinder. J. Fluids Struct. 30, 159–172.Google Scholar
Stansby, P. K. & Rainey, R. C. T. 2001 On the orbital response of a rotating cylinder in a current. J. Fluid Mech. 439, 87–108.CrossRefGoogle Scholar
Strouhal, V. 1878 Uber eine besondere art der tonerregung. Ann. Phys. Chem. New Series 5, 216–251.Google Scholar
Vicente-Ludlam, D., Barrero-Gil, A. & Velazquez, A. 2014 Optimal electromagnetic energy extraction from transverse galloping. J. Fluids Struct. 51, 281–291.Google Scholar
Vicente-Ludlam, D., Barrero-Gil, A. & Velazquez, A. 2015 Enhanced mechanical energy extraction from transverse galloping using a dual mass system. J. Sound Vib. 339, 290–303.Google Scholar
Vicente-Ludlam, D., Barrero-Gil, A. & Velazquez, A. 2017 Flow-induced vibration of a rotating circular cylinder using position and velocity feedback. J. Fluids Struct. 72, 127–151.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Xu-Xu, J., Barrero-Gil, A. & Velazquez, A. 2016 Experimental study on transverse flow-induced oscillations of a square-section cylinder at low mass ratio and low damping. Exp. Therm. Fluid Sci. 74, 286–295.CrossRefGoogle Scholar

Vicente-Ludlam et al. supplementary movie 1

Effect of rotation proportional to cylinder’s displacement.

Download Vicente-Ludlam et al. supplementary movie 1(Video)
Video 6.9 MB

Vicente-Ludlam et al. supplementary movie 2

Effect of rotation proportional to cylinder’s velocity.

Download Vicente-Ludlam et al. supplementary movie 2(Video)
Video 6.8 MB