Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T09:19:24.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow-induced motions of flexible plates: fluttering, twisting and orbital modes

Published online by Cambridge University Press:  07 February 2019

Yaqing Jin ,
Jin-Tae Kim ,
Shifeng Fu  and
Leonardo P. Chamorro Open the ORCID record for Leonardo P. Chamorro [Opens in a new window]
Yaqing Jin
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
Jin-Tae Kim
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
Shifeng Fu
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210024, China
Leonardo P. Chamorro*
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA Civil and Environmental Engineering Department, University of Illinois, Urbana, IL 61801, USA Aerospace Engineering Department, University of Illinois, Urbana, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

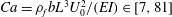The unsteady dynamics of wall-mounted flexible plates under inclined flows was fundamentally described using theoretical arguments and experiments under various Cauchy numbers $Ca=\unicode[STIX]{x1D70C}_{f}bL^{3}U_{0}^{2}/(EI)\in [7,81]$ (where 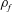$\unicode[STIX]{x1D70C}_{f}$ is the fluid density, 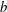$b$ and 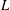$L$ are the plate width and length, 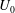$U_{0}$ is the incoming velocity, 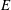$E$ is Young’s modulus and 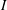$I$ is the second moment of the area) and inclination angles $\unicode[STIX]{x1D6FC}$. Three-dimensional particle tracking velocimetry and a high-resolution force sensor were used to characterize the evolution of the plate dynamics and aerodynamic force. We show the existence of three distinctive, dominant modes of tip oscillations, which are modulated by the structure dynamic and flow instability. The first mode is characterized by small-amplitude, planar fluttering-like motions occurring under a critical Cauchy number, 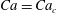$Ca=Ca_{c}$. Past this condition, the motions are dominated by the second mode consisting of unsteady twisting superimposed onto the fluttering patterns. The onset of this mode is characterized by a sharp increase of the force fluctuation intensity. At sufficiently high 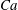$Ca$ and $\unicode[STIX]{x1D6FC}$, the plate may undergo a third mode given by large-scale tip orbits about the mean bending. Using the equation of motion and first-order approximations, we propose a formulation to estimate 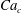$Ca_{c}$ as a function of $\unicode[STIX]{x1D6FC}$; it exhibits solid agreement with experiments.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 273 - 285
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Alben, S., Shelley, M. & Zhang, J. 2002 Drag reduction through self-similar bending of a flexible body. Nature 420 (6915), 479–481.Google Scholar
Alben, S., Shelley, M. & Zhang, J. 2004 How flexibility induces streamlining in a two-dimensional flow. Phys. Fluids 16 (5), 1694–1713.Google Scholar
Alben, S. & Shelley, M. J. 2008 Flapping states of a flag in an inviscid fluid: bistability and the transition to chaos. Phys. Rev. Lett. 100 (7), 074301.Google Scholar
Amandolese, X., Michelin, S. & Choquel, M. 2013 Low speed flutter and limit cycle oscillations of a two-degree-of-freedom flat plate in a wind tunnel. J. Fluids Struct. 43, 244–255.Google Scholar
Bhati, A., Sawanni, R., Kulkarni, K. & Bhardwaj, R. 2018 Role of skin friction drag during flow-induced reconfiguration of a flexible thin plate. J. Fluids Struct. 77, 134–150.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration. Van Nostrand Reinhold.Google Scholar
Fage, A. & Johansen, F. C. 1927 On the flow of air behind an inclined flat plate of infinite span. Proc. R. Soc. Lond. A 116 (773), 170–197.Google Scholar
Fernandes, A. C. & Armandei, M. 2014 Phenomenological model for torsional galloping of an elastic flat plate due to hydrodynamic loads. J. Hydrodyn. 26 (1), 57–65.Google Scholar
Gosselin, F., De Langre, E. L. & Machado-Almeida, B. A. 2010 Drag reduction of flexible plates by reconfiguration. J. Fluid Mech. 650, 319–341.Google Scholar
Iversen, J. D. 1979 Autorotating flat-plate wings: the effect of the moment of inertia, geometry and Reynolds number. J. Fluid Mech. 92 (02), 327–348.Google Scholar
Jia, L.-B. & Yin, X.-Z. 2008 Passive oscillations of two tandem flexible filaments in a flowing soap film. Phys. Rev. Lett. 100 (22), 228104.Google Scholar
Jin, Y. & Chamorro, L. P. 2017 Passive pitching of splitters in the trailing edge of elliptic cylinders. J. Fluid Mech. 826, 363–375.Google Scholar
Jin, Y., Hayat, I. & Chamorro, L. P. 2017 Modulation of aerodynamic force on a 2D elliptic body via passive splitter pitching under high turbulence. J. Fluids Struct. 74, 205–213.Google Scholar
Jin, Y., Ji, S., Liu, B. & Chamorro, L. P. 2016 On the role of thickness ratio and location of axis of rotation in the flat plate motions. J. Fluids Struct. 64, 127–137.Google Scholar
Jin, Y., Kim, J.-T. & Chamorro, L. P. 2018a Instability-driven frequency decoupling between structure dynamics and wake fluctuations. Phys. Rev. Fluids 3, 044701.Google Scholar
Jin, Y., Kim, J.-T., Mao, Z. & Chamorro, L. P. 2018b On the couple dynamics of wall-mounted flexible plates in tandem. J. Fluid Mech. 852, R2.Google Scholar
Kim, J.-T., Kim, D., Liberzon, A. & Chamorro, L. P. 2016 Three-dimensional particle tracking velocimetry for turbulence applications: case of a jet flow. J. Visual Exp. (108), e53745.Google Scholar
Kim, S., Huang, W.-X. & Sung, H. J. 2010 Constructive and destructive interaction modes between two tandem flexible flags in viscous flow. J. Fluid Mech. 661, 511–521.Google Scholar
Lam, K. M. 1996 Phase-locked eduction of vortex shedding in flow past an inclined flat plate. Eur. J. Mech. (B/Fluids) 8 (5), 1159–1168.Google Scholar
Lam, K. M. & Leung, M. Y. H. 2005 Asymmetric vortex shedding flow past an inclined flat plate at high incidence. Eur. J. Mech. (B/Fluids) 24, 33–48.Google Scholar
Larsen, A. 2002 Torsion galloping of elongated bluff cross sections. In ASME 2002 International Mechanical Engineering Congress and Exposition, pp. 403–409. American Society of Mechanical Engineers.Google Scholar
Leclercq, T. & De Langre, E. 2016 Drag reduction by elastic reconfiguration of non-uniform beams in non-uniform flows. J. Fluids Struct. 60, 114–129.Google Scholar
Leclercq, T., Peake, N. & de Langre, E. 2018 Does flutter prevent drag reduction by reconfiguration? Proc. R. Soc. Lond. A 474 (2209), 20170678.Google Scholar
Liu, B., Hamed, A. M., Jin, Y. & Chamorro, L. P. 2017 Influence of vortical structure impingement on the oscillation and rotation of flat plates. J. Fluids Struct. 70, 417–427.Google Scholar
Lu, L., Guo, X. L., Tang, G. Q., Liu, M. M., Chen, C. Q. & Xie, Z. H. 2016 Numerical investigation of flow-induced rotary oscillation of circular cylinder with rigid splitter plate. Phys. Fluids 28 (9), 093604.Google Scholar
Luhar, M. & Nepf, H. M. 2011 Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 56 (6), 2003–2017.Google Scholar
Mirzaeisefat, S. & Fernandes, A. C. 2013 Stability analysis of the fluttering and autorotation of flow-induced rotation of a hinged flat plate. J. Hydrodyn. 25 (5), 755–762.Google Scholar
Modi, V. J., Wiland, E., Dikshit, A. K. & Yokomizo, T. 1992 On the fluid dynamics of elliptic cylinders. In The Second International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers.Google Scholar
Onoue, K., Song, A., Strom, B. & Breuer, K. S. 2015 Large amplitude flow-induced oscillations and energy harvesting using a cyber-physical pitching plate. J. Fluids Struct. 55, 262–275.Google Scholar
Païdoussis, M. P., Price, S. J. & De Langre, E. 2010 Fluid–Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Ristroph, L. & Zhang, J. 2008 Anomalous hydrodynamic drafting of interacting flapping flags. Phys. Rev. Lett. 101 (19), 194502.Google Scholar
Schouveiler, L. & Boudaoud, A. 2006 The rolling up of sheets in a steady flow. J. Fluid Mech. 563, 71–80.Google Scholar
Schouveiler, L., Eloy, C. & Le Gal, P. 2005 Flow-induced vibrations of high mass ratio flexible filaments freely hanging in a flow. Phys. Fluids 17 (4), 047104.Google Scholar
Slater, J. E.1969 Aeroelastic instability of a structural angle section. PhD thesis, University of British Columbia.Google Scholar
Tadrist, L., Julio, K., Saudreau, M. & De Langre, E. 2015 Leaf flutter by torsional galloping: experiments and model. J. Fluids Struct. 56, 1–10.Google Scholar
Uddin, E., Huang, W.-X. & Sung, H. J. 2013 Interaction modes of multiple flexible flags in a uniform flow. J. Fluid Mech. 729, 563–583.Google Scholar

Jin et al. supplementary movie 1

Raw video illustrating small-amplitude fluttering. This sample movie is played 8x slower.

Download Jin et al. supplementary movie 1(Video)
Video 2.9 MB

Jin et al. supplementary movie 2

Raw video illustrating twisting oscillations. This sample movie is played 8x slower.

Download Jin et al. supplementary movie 2(Video)
Video 2.9 MB

Jin et al. supplementary movie 3

Raw video illustrating large-scale orbital motions. This sample movie is played 8x slower.

Download Jin et al. supplementary movie 3(Video)
Video 2.9 MB