Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-04T21:31:06.002Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow structures and heat transport in Taylor–Couette systems with axial temperature gradient

Published online by Cambridge University Press:  15 June 2021

X.-Y. Leng ,
D. Krasnov ,
B.-W. Li  and
J.-Q. Zhong Open the ORCID record for J.-Q. Zhong [Opens in a new window]
X.-Y. Leng
Affiliation:
School of Physics Science and Engineering, Tongji University, 200092Shanghai, PR China
D. Krasnov
Affiliation:
Fakultät für Maschinenbau, Technische Universität Ilmenau, Postfach 100565, 98684Ilmenau, Germany
B.-W. Li
Affiliation:
School of Energy and Power Engineering, Dalian University of Technology, 116024Dalian, PR China
J.-Q. Zhong*
Affiliation:
School of Physics Science and Engineering, Tongji University, 200092Shanghai, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

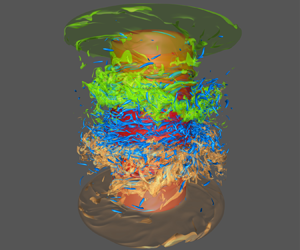
We investigate the heat transfer and coherent structures in Taylor–Couette (TC) flows that undergo thermal convection driven by an axially applied temperature gradient. Direct numerical simulations are performed in a Rayleigh number range $10^6 \leq Ra \leq 3 \times 10^8$ for Prandtl number $Pr = 4.38$ and with the shear Reynolds number up to $Re = 10^4$. When the rotation number $R_f$ increases, the flows undergo a transition from buoyancy-dominated ($R_f<1$) to shear-dominated convection ($R_f>1$). In the buoyancy-dominated regime with weak rotations, the flow features are similar to those in Rayleigh–Bénard (RB) convection with large-scale plumes emanating from the thermal boundary layers. In this regime, the $Re$-dependence of heat transport $Nu$ is sensitive to $Ra$. We find that for low $Ra$, $Nu$ decreases with increasing $Re$ and becomes independent of $Re$ at high $Ra$. In the shear-dominated regime, the flow structures are characterised by Taylor vortices (TVs), which effectively enhance the heat transport. With sufficiently high Reynolds number for $2000< Re \le 10\,000$, the flow structures are dominated by turbulent TVs, and the transport scaling laws of heat and angular velocity fluxes become independent of buoyancy. We report that in this turbulent regime the axial heat-transport scaling $(Nu\sim Re^{0.578\pm 0.018})$ is consistent with the scaling of radial angular-momentum transport $(Nu_{\omega }\sim Re^{0.581\pm 0.026})$.

JFM classification

Turbulent Flows: Turbulent convection Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , A42
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adams, J.C., Swarztrauber, P. & Sweet, R. 1999 Efficient fortran subprograms for the solution of separable elliptic partial differential equations. https://www2.cisl.ucar.edu/resources/legacy/fishpack/.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Akhmedagaev, R., Zikanov, O., Krasnov, D. & Schumacher, J. 2020 Turbulent Rayleigh–Bénard convection in a strong vertical magnetic field. J. Fluid Mech. 895, R4.CrossRefGoogle Scholar
Akonur, A. & Lueptow, R.M. 2002 Chaotic mixing and transport in wavy Taylor–Couette flow. Physica D 167 (3–4), 183–196.CrossRefGoogle Scholar
Akonur, A. & Lueptow, R.M. 2003 Three-dimensional velocity field for wavy Taylor–Couette flow. Phys. Fluids 15 (4), 947–960.CrossRefGoogle Scholar
Andereck, C.D., Liu, S.S. & Swinney, H.L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Batchelor, G.K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5 (1), 113–133.CrossRefGoogle Scholar
Bergman, T.L., Incropera, F.P., DeWitt, D.P. & Lavine, A.S. 2011 Fundamentals of Heat and Mass Transfer. John Wiley & Sons.Google Scholar
Bilson, M. & Bremhorst, K. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 579, 227–270.CrossRefGoogle Scholar
Blass, A., Zhu, X.J., Verzicco, R., Lohse, D. & Stevens, R.J.A.M. 2020 Flow organization and heat transfer in turbulent wall sheared thermal convection. J. Fluid Mech. 897, A22.CrossRefGoogle ScholarPubMed
Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36 (1), 177–191.CrossRefGoogle Scholar
Busse, F.H. 2012 The twins of turbulence research. Physics 5, 4.CrossRefGoogle Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover Publications.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 1–25.CrossRefGoogle ScholarPubMed
Chong, K.L., Yang, Y.T., Huang, S.D., Zhong, J.Q., Stevens, R.J.A.M., Verzicco, R., Lohse, D. & Xia, K.Q. 2017 Confined Rayleigh–Bénard, rotating Rayleigh–Bénard, and double diffusive convection: a unifying view on turbulent transport enhancement through coherent structure manipulation. Phys. Rev. Lett. 119 (6), 064501.CrossRefGoogle ScholarPubMed
Dong, S. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 587, 373–393.CrossRefGoogle Scholar
Dubrulle, B. & Hersant, F. 2002 Momentum transport and torque scaling in Taylor–Couette flow from an analogy with turbulent convection. Eur. Phys. J. B 26 (3), 379–386.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.CrossRefGoogle Scholar
Emran, M.S. & Schumacher, J. 2008 Fine-scale statistics of temperature and its derivatives in convective turbulence. J. Fluid Mech. 611, 13–34.CrossRefGoogle Scholar
Fardin, M.A., Perge, C. & Taberlet, N. 2014 “The hydrogen atom of fluid dynamics” – introduction to the Taylor–Couette flow for soft matter scientists. Soft Matt. 10 (20), 3523–3535.CrossRefGoogle ScholarPubMed
Froitzheim, A., Merbold, S., Ostilla-Mónico, R. & Egbers, C. 2019 Angular momentum transport and flow organization in Taylor–Couette flow at radius ratio of $\eta =0.357$. Phys. Rev. Fluids 4, 084605.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High-Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48 (1), 53–80.CrossRefGoogle Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh–Bénard convection. J. Comput. Phys. 49 (2), 241–264.CrossRefGoogle Scholar
Guillerm, R., Kang, C., Savaro, C., Lepiller, V., Prigent, A., Yang, K.-S. & Mutabazi, I. 2015 Flow regimes in a vertical Taylor–Couette system with a radial thermal gradient. Phys. Fluids 27 (9), 094101.CrossRefGoogle Scholar
Ji, H.T., Burin, M., Schartman, E. & Goodman, J. 2006 Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444 (7117), 343–346.CrossRefGoogle ScholarPubMed
Kang, C., Meyer, A., Mutabazi, I. & Yoshikawa, H.N. 2017 Radial buoyancy effects on momentum and heat transfer in a circular Couette flow. Phys. Rev. Fluids 2, 053901.CrossRefGoogle Scholar
Kang, C., Yang, K.-S & Mutabazi, I. 2015 Thermal effect on large-aspect-ratio Couette–Taylor system: numerical simulations. J. Fluid Mech. 771, 57–78.CrossRefGoogle Scholar
Kataoka, K. & Takigawa, T. 1981 Intermixing over cell boundary between Taylor vortices. AIChE J. 27 (3), 504–508.CrossRefGoogle Scholar
Kays, W.M. & Crawford, M.S. 1980 Convective heat and mass transfer. McGraw-Hill.Google Scholar
King, E.M. & Aurnou, J.M. 2015 Magnetostrophic balance as the optimal state for turbulent magnetoconvection. Proc. Natl Acad. Sci. 112 (4), 990–994.CrossRefGoogle ScholarPubMed
Kirillov, O.N. & Mutabazi, I. 2017 Short-wavelength local instabilities of a circular Couette flow with radial temperature gradient. J. Fluid Mech. 818, 319–343.CrossRefGoogle Scholar
Koschmieder, E.L. 1993 Bénard cells and Taylor vortices. Cambridge University Press.Google Scholar
Krasnov, D., Thess, A., Boeck, T., Zhao, Y. & Zikanov, O. 2013 Patterned turbulence in liquid metal flow: computational reconstruction of the hartmann experiment. Phys. Rev. Lett. 110, 084501.CrossRefGoogle ScholarPubMed
Krasnov, D., Zikanov, O. & Boeck, T. 2011 Comparative study of finite difference approaches in simulation of magnetohydrodynamic turbulence at low magnetic Reynolds number. Comput. Fluids 50 (1), 46–59.CrossRefGoogle Scholar
Lathrop, D.P., Fineberg, J. & Swinney, H.L. 1992 a Transition to shear-driven turbulence in Couette–Taylor flow. Phys. Rev. A 46 (10), 6390.CrossRefGoogle ScholarPubMed
Lathrop, D.P., Fineberg, J. & Swinney, H.L. 1992 b Turbulent flow between concentric rotating cylinders at large Reynolds number. Phys. Rev. Lett. 68 (10), 1515.CrossRefGoogle ScholarPubMed
Leng, X.Y., Kolesnikov, Y.B., Krasnov, D. & Li, B.W. 2018 Numerical simulation of turbulent Taylor–Couette flow between conducting cylinders in an axial magnetic field at low magnetic Reynolds number. Phys. Fluids 30 (1), 015107.CrossRefGoogle Scholar
Lim, Z.L., Chong, K.L., Ding, G.Y. & Xia, K.Q. 2019 Quasistatic magnetoconvection: heat transport enhancement and boundary layer crossing. J. Fluid Mech. 870, 519–542.CrossRefGoogle Scholar
Lohse, D. & Xia, K.Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Merbold, S., Brauckmann, H.J. & Egbers, C. 2013 Torque measurements and numerical determination in differentially rotating wide gap Taylor–Couette flow. Phys. Rev. E 87, 023014.CrossRefGoogle ScholarPubMed
Ostilla-Mónico, R., Huisman, S.G., Jannink, T.J.G., Van Gils, D.P.M., Verzicco, R., Grossmann, S., Sun, C. & Lohse, D. 2014 Optimal Taylor–Couette flow: radius ratio dependence. J. Fluid Mech. 747, 1–29.CrossRefGoogle Scholar
Ostilla-Mónico, R., Van Der Poel, E.P, Verzicco, R., Grossmann, S. & Lohse, D. 2014 Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Scagliarini, A., Gylfason, Á. & Toschi, F. 2014 Heat-flux scaling in turbulent Rayleigh–Bénard convection with an imposed longitudinal wind. Phys. Rev. E 89 (4), 043012.CrossRefGoogle ScholarPubMed
Scheel, J.D., Emran, M.S. & Schumacher, J. 2013 Resolving the fine-scale structure in turbulent Rayleigh–Bénard convection. New J. Phys. 15 (11), 113063.CrossRefGoogle Scholar
Shishkina, O., Stevens, R.J.A.M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.CrossRefGoogle Scholar
Shraiman, B.I. & Siggia, E.D 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42 (6), 3650.CrossRefGoogle ScholarPubMed
Singh, H., Bonnesoeur, A., Besnard, H., Houssin, C., Prigent, A., Crumeyrolle, O. & Mutabazi, I. 2019 A large thermal turbulent Taylor–Couette (THETACO) facility for investigation of turbulence induced by simultaneous action of rotation and radial temperature gradient. Rev. Sci. Instrum. 90 (11), 115112.CrossRefGoogle ScholarPubMed
Stevens, R.J.A.M., Van der Poel, E.P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730 (5), 295–308.CrossRefGoogle Scholar
Stevens, R.J.A.M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
Taylor, G.I. 1923 Stability of viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. 223, 289–343.Google Scholar
Van Der Veen, R.C.A., Huisman, S.G., Merbold, S., Harlander, U., Egbers, C., Lohse, D. & Sun, C. 2016 Taylor–Couette turbulence at radius ratio $\eta =0.5$: scaling, flow structures and plumes. J. Fluid Mech. 799, 334–351.CrossRefGoogle Scholar
Wen, J., Zhang, W.-Y., Ren, L.-Z., Bao, L.-Y., Dini, D., Xi, H.D. & Hu, H.-B. 2020 Controlling the number of vortices and torque in Taylor–Couette flow. J. Fluid Mech. 901, A30.CrossRefGoogle Scholar
Yoshikawa, H.N., Nagata, M. & Mutabazi, I. 2013 Instability of the vertical annular flow with a radial heating and rotating inner cylinder. Phys. Fluids 25 (11), 114104.CrossRefGoogle Scholar
Zhong, J.Q., Stevens, R.J.A.M., Clercx, H.J.H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102 (4), 044502.CrossRefGoogle ScholarPubMed
Zhu, X., Jiang, L.F., Zhou, Q. & Sun, C. 2019 Turbulent Rayleigh–Bénard convection in an annular cell. J. Fluid Mech. 869, R5.CrossRefGoogle Scholar

Leng et al. supplementary movie 1

See pdf for movie caption

Download Leng et al. supplementary movie 1(Video)
Video 3.5 MB

Leng et al. supplementary movie 2

See pdf file for movie caption

Download Leng et al. supplementary movie 2(Video)
Video 3.4 MB

Leng et al. supplementary movie 3

See pdf file for movie caption

Download Leng et al. supplementary movie 3(Video)
Video 3.5 MB

Leng et al. supplementary movie 4

See pdf file for movie caption

Download Leng et al. supplementary movie 4(Video)
Video 2.1 MB
Supplementary material: PDF

Leng et al. supplementary material

Captions for movies 1-4

Download Leng et al. supplementary material(PDF)
PDF 13.1 KB