No CrossRef data available.
Published online by Cambridge University Press: 25 November 2024
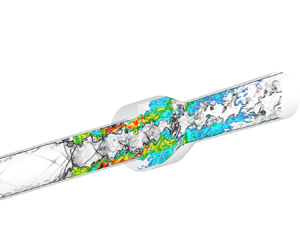
This study investigates the flow structures and combustion regimes in an axisymmetric cavity-based scramjet combustor with a total temperature of 1800 K and a high Reynolds number of approximately 1 × 107. The hydroxyl planar laser-induced fluorescence technique, along with the broadband flame emission and CH* chemiluminescence, is employed to visualize the instantaneous flame structure in the optically accessible cavity. The jet-wake flame stabilization mode is observed, with intense heat release occurring in the jet wake upstream of the cavity. A hybrid Reynolds-averaged Navier–Stokes/large-eddy simulation approach is performed for the 0.18-equivalent-ratio case with a pressure-corrected flamelet/progress variable model. The combustion regime is identified mainly in the corrugated or wrinkled flamelet regime (approximately 102 < Da < 104, 103 < Ret < 105 where  $Da$ is the Damköhler number and
$Da$ is the Damköhler number and  $Re_t$ is the turbulent Reynolds number). The combustion process is jointly dominated by supersonic combustion (which accounts for approximately 58 %) and subsonic combustion, although subsonic combustion has a higher heat release rate (peak value exceeding 1 × 109 J (m3s)−1). A partially premixed flame is observed, where the diffusion flame packages a considerable quantity of twisted premixed flame. The shockwave plays a critical role in generating vorticity by strengthening the volumetric expansion and baroclinic torque term, and it can facilitate the chemical reaction rates through the pressure and temperature surges, thereby enhancing the combustion. Combustion also shows a remarkable effect on the overall flow structures, and it drives alterations in the vorticity of the flow field. In turn, the turbulent flow facilitates the combustion and improves the flame stabilization by enhancing the reactant mixing and increasing the flame surface area.
$Re_t$ is the turbulent Reynolds number). The combustion process is jointly dominated by supersonic combustion (which accounts for approximately 58 %) and subsonic combustion, although subsonic combustion has a higher heat release rate (peak value exceeding 1 × 109 J (m3s)−1). A partially premixed flame is observed, where the diffusion flame packages a considerable quantity of twisted premixed flame. The shockwave plays a critical role in generating vorticity by strengthening the volumetric expansion and baroclinic torque term, and it can facilitate the chemical reaction rates through the pressure and temperature surges, thereby enhancing the combustion. Combustion also shows a remarkable effect on the overall flow structures, and it drives alterations in the vorticity of the flow field. In turn, the turbulent flow facilitates the combustion and improves the flame stabilization by enhancing the reactant mixing and increasing the flame surface area.