Published online by Cambridge University Press: 24 October 2013
Flow past a circular cylinder executing sinusoidal rotary oscillations about its own axis is studied experimentally. The experiments are carried out at a Reynolds number of 185, oscillation amplitudes varying from  $\mathrm{\pi} / 8$ to
$\mathrm{\pi} / 8$ to 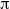 $\mathrm{\pi} $, and at non-dimensional forcing frequencies (ratio of the cylinder oscillation frequency to the vortex-shedding frequency from a stationary cylinder) varying from 0 to 5. The diagnostic is performed by extensive flow visualization using the hydrogen bubble technique, hot-wire anemometry and particle-image velocimetry. The wake structures are related to the velocity spectra at various forcing parameters and downstream distances. It is found that the phenomenon of lock-on occurs in a forcing frequency range which depends not only on the amplitude of oscillation but also the downstream location from the cylinder. The experimentally measured lock-on diagram in the forcing amplitude and frequency plane at various downstream locations ranging from 2 to 23 diameters is presented. The far-field wake decouples, after the lock-on at higher forcing frequencies and behaves more like a regular Bénard–von Kármán vortex street from a stationary cylinder with vortex-shedding frequency mostly lower than that from a stationary cylinder. The dependence of circulation values of the shed vortices on the forcing frequency reveals a decay character independent of forcing amplitude beyond forcing frequency of
$\mathrm{\pi} $, and at non-dimensional forcing frequencies (ratio of the cylinder oscillation frequency to the vortex-shedding frequency from a stationary cylinder) varying from 0 to 5. The diagnostic is performed by extensive flow visualization using the hydrogen bubble technique, hot-wire anemometry and particle-image velocimetry. The wake structures are related to the velocity spectra at various forcing parameters and downstream distances. It is found that the phenomenon of lock-on occurs in a forcing frequency range which depends not only on the amplitude of oscillation but also the downstream location from the cylinder. The experimentally measured lock-on diagram in the forcing amplitude and frequency plane at various downstream locations ranging from 2 to 23 diameters is presented. The far-field wake decouples, after the lock-on at higher forcing frequencies and behaves more like a regular Bénard–von Kármán vortex street from a stationary cylinder with vortex-shedding frequency mostly lower than that from a stationary cylinder. The dependence of circulation values of the shed vortices on the forcing frequency reveals a decay character independent of forcing amplitude beyond forcing frequency of  ${\sim }1. 0$ and a scaling behaviour with forcing amplitude at forcing frequencies
${\sim }1. 0$ and a scaling behaviour with forcing amplitude at forcing frequencies 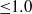 ${\leq }1. 0$. The flow visualizations reveal that the far-field wake becomes two-dimensional (planar) near the forcing frequencies where the circulation of the shed vortices becomes maximum and strong three-dimensional flow is generated as mode shape changes in certain forcing parameter conditions. It is also found from flow visualizations that even at higher Reynolds number of 400, forcing the cylinder at forcing amplitudes of
${\leq }1. 0$. The flow visualizations reveal that the far-field wake becomes two-dimensional (planar) near the forcing frequencies where the circulation of the shed vortices becomes maximum and strong three-dimensional flow is generated as mode shape changes in certain forcing parameter conditions. It is also found from flow visualizations that even at higher Reynolds number of 400, forcing the cylinder at forcing amplitudes of 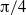 $\mathrm{\pi} / 4$ and
$\mathrm{\pi} / 4$ and 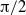 $\mathrm{\pi} / 2$ can make the flow field two-dimensional at forcing frequencies greater than
$\mathrm{\pi} / 2$ can make the flow field two-dimensional at forcing frequencies greater than 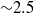 ${\sim }2. 5$.
${\sim }2. 5$.
Caption: Far wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 0.8 at Re = 185.
Caption: Far wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 0.25 at Re = 185.
Caption: Far wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 1.0 at Re = 185.
Caption: Far wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 4.5 at Re = 185.
Caption: Near wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 0.8 at Re = 185.
Caption: Near wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 0.25 at Re = 185.
Caption: Near wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 1.0 at Re = 185.