Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T17:59:42.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow past a circular cylinder and a downstream sphere for Re < 300

Published online by Cambridge University Press:  01 March 2021

Ming Zhao Open the ORCID record for Ming Zhao [Opens in a new window]
Ming Zhao*
Affiliation:
School of Engineering, Western Sydney University, Penrith2751, NSWAustralia
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

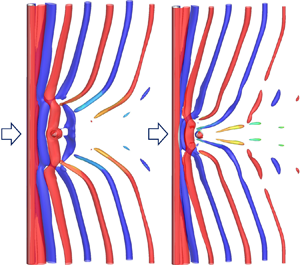
Flow past a circular cylinder and a downstream sphere is simulated numerically for Reynolds numbers between 100 and 300 for cylinder-to-sphere gap ratios between 0 and 3. The aim of this study is to investigate the influence of the sphere on the vortex shedding of the cylinder, and the wake-induced forces on the sphere. If vortices are shed from the cylinder upstream of the sphere, vortices are disconnected after they pass the sphere. This type of vortex disconnection is defined as sphere-induced vortex disconnection. The key finding is the so-called sphere-induced vortex dislocation (SIVDL) which occurs within the vortex formation region. The main characteristics of SIVDL include the adhesion of vortices to the cylinder at dislocation positions, and periodical occurrences of SIVDL. The periodic occurrence of SIVDL makes the frequency of vortex shedding change over time. Another interesting phenomenon is the reattachment of the separated shear layers from the cylinder to the sphere, which occurs when the sphere–cylinder gap is small. This leads to the formation of vortices without disconnection downstream of the sphere that it is similar to the case of tandem cylinders. In all cases, vortices are inclined, and their angle of inclination increases when SIVDL occurs. SIVDL reduces the frequency of the lift coefficient and increases the standard deviation of the drag coefficient of the sphere. The periodic occurrence of SIVDL causes the beating of the lift coefficient along with large-amplitude, low-frequency oscillations of the sphere's drag coefficient.

JFM classification

Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A20
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M.M., Moriya, M., Takai, K. & Sakamoto, H. 2003 Fluctuating fluid forces acting on two circular cylinders in a tandem arrangement at a subcritical Reynolds number. J. Wind Engng Ind Aerodyn 91, 139–154.CrossRefGoogle Scholar
Behara, S., Borazjani, I. & Sotiropoulos, F. 2011 Vortex-induced vibrations of an elastically mounted sphere with three degrees of freedom at Re = 300: hysteresis and vortex shedding modes. J. Fluid Mech. 686, 426–450.CrossRefGoogle Scholar
Behr, M., Hastreiter, D., Mittal, S. & Tezduyar, T.E. 1995 Incompressible flow past a circular cylinder: dependence of the computed flow field on the location of the lateral boundaries. Comput. Meth. Appl. Mech. Engng 123, 309–316.CrossRefGoogle Scholar
Blackburn, H.M. 2002 Mass and momentum transport from a sphere in steady and oscillatory flows. Phys. Fluids 14, 3997–4011.CrossRefGoogle Scholar
Carmo, B.S., Meneghini, J.R. & Sherwin, S.J. 2010 a Possible states in the flow around two circular cylinders in tandem with separations in the vicinity of the drag inversion spacing. Phys. Fluids 22, 1–7.CrossRefGoogle Scholar
Carmo, B.S., Meneghini, J.R. & Sherwin, S.J. 2010 b Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.CrossRefGoogle Scholar
Chopra, G. & Mittal, S. 2019 Drag coefficient and formation length at the onset of vortex shedding. Phys. Fluids 31, 013601.CrossRefGoogle Scholar
Dunn, W. & Tavoularis, S. 2006 Experimental studies of vortices shed from cylinders with a step-change in diameter. J. Fluid Mech. 555, 409–437.CrossRefGoogle Scholar
Giacobello, M., Ooi, A. & Balachandar, S. 2009 Wake structure of a transversely rotating sphere at moderate Reynolds numbers. J. Fluid Mech. 621, 103–130.CrossRefGoogle Scholar
Henderson, R.D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
Igarashi, T. 1981 Characteristics of the flow around two circular cylinders arranged in tandem - 1. Bull. JSME 24, 323–331.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Ji, C., Yang, X., Yu, Y., Cui, Y. & Srinil, N. 2020 Numerical simulations of flows around a dual step cylinder with different diameter ratios at low Reynolds number. Eur. J. Mech. (B/Fluids) 79, 332–344.CrossRefGoogle Scholar
Jiang, H., Cheng, L. & An, H. 2018 Three-dimensional wake transition of a square cylinder. J. Fluid Mech. 842, 102–127.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016 Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.CrossRefGoogle Scholar
Johnson, T.A. & Patel, V.C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
Kim, D. 2009 Laminar flow past a sphere rotating in the transverse direction. J. Mech. Sci. Technol. 23, 578–589.CrossRefGoogle Scholar
Koda, Y. & Lien, F.S. 2013 Aerodynamic effects of the early three-dimensional instabilities in the flow over one and two circular cylinders in tandem predicted by the lattice Boltzmann method. Comput. Fluids 74, 32–43.CrossRefGoogle Scholar
Leweke, T. & Williamson, C.H.K. 1998 Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17, 571–586.CrossRefGoogle Scholar
Magnaudet, J., Fabre, J. & Rivero, M. 1995 Accelerated flows past a rigid sphere or a spherical bubble. Part 1. Steady straining flow. J. Fluid Mech. 284, 97–135.CrossRefGoogle Scholar
Miller, G.D. & Williamson, C.H.K. 1994 Control of three-dimensional phase dynamics in a cylinder wake. Exp. Fluids 18, 26–35.CrossRefGoogle Scholar
Mittal, R. 1999 Planar symmetry in the unsteady wake of a sphere. AIAA J. 37, 388–390.CrossRefGoogle Scholar
Morton, C. & Yarusevych, S. 2010 Vortex shedding in the wake of a step cylinder. Phys. Fluids 22.CrossRefGoogle Scholar
Ormières, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83, 80–83.CrossRefGoogle Scholar
Papaioannou, G.V., Yue, D.K.P., Triantafyllou, M.S. & Karniadakis, G.E. 2006 Three- dimensionality effects in flow around two tandem cylinders. J. Fluid Mech. 558, 387–413.CrossRefGoogle Scholar
Parnaudeau, P., Heitz, D., Lamballais, E. & Silvestrini, J.H. 2007 Direct numerical simulations of vortex shedding behind cylinders with spanwise linear nonuniformity. J. Turbul. 8, 1–13.CrossRefGoogle Scholar
Poon, E.K.W., Ooi, A.S.H., Giacobello, M. & Cohen, R.C.Z. 2010 Laminar flow structures from a rotating sphere: effect of rotating axis angle. Intl J. Heat Fluid Flow 31, 961–972.CrossRefGoogle Scholar
Rajamuni, M.M., Thompson, M.C. & Hourigan, K. 2018 Transverse flow-induced vibrations of a sphere. J. Fluid Mech. 837, 931–966.CrossRefGoogle Scholar
Rajamuni, M.M., Thompson, M.C. & Hourigan, K. 2019 Vortex-induced vibration of elastically- mounted spheres: a comparison of the response of three degrees of freedom and one degree of freedom systems. J. Fluids Struct. 89, 142–155.CrossRefGoogle Scholar
Rao, A., Thompson, M.C. & Hourigan, K. 2016 A universal three-dimensional instability of the wakes of two-dimensional bluff bodies. J. Fluid Mech. 792, 50–66.CrossRefGoogle Scholar
Rao, A., Thompson, M.C., Leweke, T. & Hourigan, K. 2013 a Dynamics and stability of the wake behind tandem cylinders sliding along a wall. J. Fluid Mech. 722, 291–316.CrossRefGoogle Scholar
Rao, A., Thompson, M.C., Leweke, T. & Hourigan, K. 2013 b The flow past a circular cylinder translating at different heights above a wall. J. Fluids Struct. 41, 9–21.CrossRefGoogle Scholar
Roos, F.W. & Willmarth, W.W. 1971 Some experimental results on sphere and disk drag. AIAA J. 9, 285–291.CrossRefGoogle Scholar
Sharman, B., Lien, F.S., Davidson, L. & Norberg, C. 2005 Numerical predictions of low Reynolds number flows over two tandem circular cylinders. Intl J. Numer. Meth. Fluids 47, 423–447.CrossRefGoogle Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1998 Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition. Intl J. Numer. Meth. Fluids 26, 39–56.3.0.CO;2-P>CrossRefGoogle Scholar
Sumer, B.M. & Fredsøe, J. 2006 Hydrodynamics Around Cylindrical Structures. World Scientific.CrossRefGoogle Scholar
Sumner, D. 2010 Two circular cylinders in cross-flow: a review. J. Fluids Struct. 26, 849–899.CrossRefGoogle Scholar
Tezduyar, T.E. & Shih, R. 1991 Numerical experiments on downstream boundary of flow past cylinder. J. Engng Mech. 117, 854–871.Google Scholar
Thapa, J., Zhao, M., Cheng, L. & Zhou, T. 2015 Three-dimensional simulations of flow past two circular cylinders in side-by-side arrangements at right and oblique attacks. J. Fluids Struct. 55, 64–83.CrossRefGoogle Scholar
Thompson, M., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.CrossRefGoogle Scholar
Tomboulides, A.G. 1993 Direct and large-eddy simulation of wake flows: flow past a sphere. PhD Thesis, Princeton University.CrossRefGoogle Scholar
Tong, F., Cheng, L. & Zhao, M. 2015 Numerical simulations of steady flow past two cylinders in staggered arrangements. J. Fluid Mech. 765, 114–149.CrossRefGoogle Scholar
Wang, Y.T., Yan, Z.M. & Wang, H.M. 2013 Numerical simulation of low-Reynolds number flows past two tandem cylinders of different diameters. Water Sci. Engng 6, 433–445.Google Scholar
Williamson, C.H.K. 1988 a Defining a universal and continuous Strouhal-Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31, 2742–2744.CrossRefGoogle Scholar
Williamson, C.H.K. 1988 b The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.CrossRefGoogle Scholar
Williamson, C.H.K. 1992 The natural and forced formation of spot-like ‘vortex dislocations’ in the transition of a wake. J. Fluid Mech. 243, 393–441.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid. Mech. 28, 477–539.CrossRefGoogle Scholar
Zhang, H.Q., Fey, U., Noack, B.R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7, 779–794.CrossRefGoogle Scholar
Zhao, M., Cheng, L. & Zhou, T. 2009 Direct numerical simulation of three-dimensional flow past a yawed circular cylinder of infinite length. J. Fluids Struct. 25, 831–847.CrossRefGoogle Scholar
Zhao, M., Thapa, J., Cheng, L. & Zhou, T. 2013 Three-dimensional transition of vortex shedding flow around a circular cylinder at right and oblique attacks. Phys. Fluids 25.CrossRefGoogle Scholar
Zdravkovich, M.M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.CrossRefGoogle Scholar