Published online by Cambridge University Press: 14 September 2009
Non-Oberbeck–Boussinesq (NOB) effects on the flow organization in two-dimensional Rayleigh–Bénard turbulence are numerically analysed. The working fluid is water. We focus on the temperature profiles, the centre temperature, the Nusselt number and on the analysis of the velocity field. Several velocity amplitudes (or Reynolds numbers) and several kinetic profiles are introduced and studied; these together describe the various features of the rather complex flow organization. The results are presented both as functions of the Rayleigh number Ra (with Ra up to 108) for fixed temperature difference Δ between top and bottom plates and as functions of Δ (‘non-Oberbeck–Boussinesqness’) for fixed Ra with Δ up to 60K. All results are consistent with the available experimental NOB data for the centre temperature Tc and the Nusselt number ratio NuNOB/NuOB (the label OB meaning that the Oberbeck–Boussinesq conditions are valid). For the temperature profiles we find – due to plume emission from the boundary layers – increasing deviations from the extended Prandtl–Blasius boundary layer theory presented in Ahlers et al. (J. Fluid Mech., vol. 569, 2006, p. 409) with increasing Ra, while the centre temperature itself is surprisingly well predicted by that theory. For given non-Oberbeck–Boussinesqness Δ, both the centre temperature Tc and the Nusselt number ratio NuNOB/NuOB only weakly depend on Ra in the Ra range considered here.
Beyond Ra ≈ 106 the flow consists of a large diagonal centre convection roll and two smaller rolls in the upper and lower corners, respectively (‘corner flows’). Also in the NOB case the centre convection roll is still characterized by only one velocity scale. In contrast, the top and bottom corner flows are then of different strengths, the bottom one being a factor 1.3 faster (for Δ = 40K) than the top one, due to the lower viscosity in the hotter bottom boundary layer. Under NOB conditions the enhanced lower corner flow as well as the enhanced centre roll lead to an enhancement of the volume averaged energy based Reynolds number 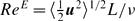 of about 4% to 5% for Δ = 60K. Moreover, we find
of about 4% to 5% for Δ = 60K. Moreover, we find 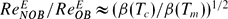 , with β the thermal expansion coefficient and Tm the arithmetic mean temperature between top and bottom plate temperatures. This corresponds to the ratio of the free fall velocities at the respective temperatures. By artificially switching off the temperature dependence of β in the numerics, the NOB modifications of ReE is less than 1% even at Δ = 60K, revealing the temperature dependence of the thermal expansion coefficient as the main origin of the NOB effects on the global Reynolds number in water.
, with β the thermal expansion coefficient and Tm the arithmetic mean temperature between top and bottom plate temperatures. This corresponds to the ratio of the free fall velocities at the respective temperatures. By artificially switching off the temperature dependence of β in the numerics, the NOB modifications of ReE is less than 1% even at Δ = 60K, revealing the temperature dependence of the thermal expansion coefficient as the main origin of the NOB effects on the global Reynolds number in water.