Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-16T18:02:22.417Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow onset for a single bubble in a yield-stress fluid

Published online by Cambridge University Press:  23 December 2021

Ali Pourzahedi ,
Emad Chaparian Open the ORCID record for Emad Chaparian [Opens in a new window] ,
Ali Roustaei  and
Ian A. Frigaard Open the ORCID record for Ian A. Frigaard [Opens in a new window]
Ali Pourzahedi
Affiliation:
Department of Mechanical Engineering, University of British Columbia, 2054-6250 Applied Science Lane, Vancouver, BC V6T 1Z4, Canada
Emad Chaparian*
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC V6T 1Z2, Canada
Ali Roustaei*
Affiliation:
School of Engineering Science, College of Engineering, University of Tehran, Tehran 14155-6619, Iran
Ian A. Frigaard
Affiliation:
Department of Mechanical Engineering, University of British Columbia, 2054-6250 Applied Science Lane, Vancouver, BC V6T 1Z4, Canada Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC V6T 1Z2, Canada
*
†Email addresses for correspondence: [email protected]; [email protected]
†Email addresses for correspondence: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

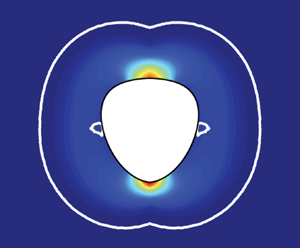
We use computational methods to determine the minimal yield stress required in order to hold static a buoyant bubble in a yield-stress liquid. The static limit is governed by the bubble shape, the dimensionless surface tension ($\gamma$) and the ratio of the yield stress to the buoyancy stress ($Y$). For a given geometry, bubbles are static for $Y > Y_c$, which we determine for a range of shapes. Given that surface tension is negligible, long prolate bubbles require larger yield stress to hold static compared with oblate bubbles. Non-zero $\gamma$ increases $Y_c$ and for large $\gamma$ the yield-capillary number ($Y/\gamma$) determines the static boundary. In this limit, although bubble shape is important, bubble orientation is not. Two-dimensional planar and axisymmetric bubbles are studied.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Non-Newtonian Flows: Plastic materials Drops and Bubbles: Bubble dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 933 , 25 February 2022 , A21
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahmadi, A. & Karimfazli, I. 2021 A quantitative evaluation of viscosity regularization in predicting transient flows of viscoplastic fluids. J. Non-Newtonian Fluid Mech. 287, 104429.CrossRefGoogle Scholar
Astarita, G. & Apuzzo, G. 1965 Motion of gas bubbles in non-Newtonian liquids. AIChE J. 11 (5), 815–820.CrossRefGoogle Scholar
Balmforth, N., Frigaard, I.A. & Ovarlez, G. 2014 Yielding to stress: recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 46, 121–146.CrossRefGoogle Scholar
Beris, A.N., Tsamopoulos, J., Armstrong, R.C. & Brown, R.A. 1985 Creeping motion of a sphere through a Bingham plastic. J. Fluid Mech. 158, 219–244.CrossRefGoogle Scholar
Boudreau, B.P. 2012 The physics of bubbles in surficial, soft, cohesive sediments. Mar. Petrol. Geol. 38 (1), 1–18.CrossRefGoogle Scholar
Burgos, G., Alexandrou, A. & Entov, V. 1999 On the determination of yield surfaces in Herschel–Bulkley fluids. J. Rheol. 43 (3), 463–483.CrossRefGoogle Scholar
Chakrabarty, J. 2012 Theory of Plasticity. Butterworth-Heinemann.Google Scholar
Chaparian, E. & Frigaard, I.A. 2017 a Cloaking: particles in a yield-stress fluid. J. Non-Newtonian Fluid Mech. 243, 47–55.CrossRefGoogle Scholar
Chaparian, E. & Frigaard, I.A. 2017 b Yield limit analysis of particle motion in a yield-stress fluid. J. Fluid Mech. 819, 311–351.CrossRefGoogle Scholar
Chaparian, E. & Frigaard, I.A. 2021 Clouds of bubbles in a viscoplastic fluid. J. Fluid Mech. 927, R3.CrossRefGoogle Scholar
Chaparian, E., Izbassarov, D., De Vita, F., Brandt, L. & Tammisola, O. 2020 Yield-stress fluids in porous media: a comparison of viscoplastic and elastoviscoplastic flows. Meccanica 55 (2), 331–342.CrossRefGoogle ScholarPubMed
Chaparian, E. & Nasouri, B. 2018 L-box—a tool for measuring the “yield stress”: a theoretical study. Phys. Fluids 30 (8), 083101.CrossRefGoogle Scholar
Chaparian, E. & Tammisola, O. 2021 Sliding flows of yield-stress fluids. J. Fluid Mech. 911, A17.CrossRefGoogle Scholar
Deoclecio, L.H.P., Soares, E.J., Deka, H. & Pierson, J.-L. 2021 Bubble entrapment condition in Bingham materials. J. Non-Newtonian Fluid Mech. 295, 104616.CrossRefGoogle Scholar
Derakhshandeh, B. 2016 Kaolinite suspension as a model fluid for fluid dynamics studies of fluid fine tailings. Rheol. Acta 55 (9), 749–758.CrossRefGoogle Scholar
Dimakopoulos, Y., Pavlidis, M. & Tsamopoulos, J. 2013 Steady bubble rise in Herschel–Bulkley fluids and comparison of predictions via the augmented Lagrangian method with those via the Papanastasiou model. J. Non-Newtonian Fluid Mech. 200, 34–51.CrossRefGoogle Scholar
Dubash, N., Balmforth, N., Slim, A. & Cochard, S. 2009 What is the final shape of a viscoplastic slump? J. Non-Newtonian Fluid Mech. 158 (1–3), 91–100.CrossRefGoogle Scholar
Dubash, N. & Frigaard, I. 2004 Conditions for static bubbles in viscoplastic fluids. Phys. Fluids 16 (12), 4319–4330.CrossRefGoogle Scholar
Dubash, N. & Frigaard, I.A. 2007 Propagation and stopping of air bubbles in Carbopol solutions. J. Non-Newtonian Fluid Mech. 142 (1–3), 123–134.CrossRefGoogle Scholar
Duvaut, G. & Lions, J.L. 1976 Inequalities in Mechanics and Physics. Springer.CrossRefGoogle Scholar
Frigaard, I.A. & Nouar, C. 2005 On the usage of viscosity regularisation methods for visco-plastic fluid flow computation. J. Non-Newtonian Fluid Mech. 127 (1), 1–26.CrossRefGoogle Scholar
Gauglitz, P.A., Rassat, S.D., Bredt, P.R., Konynenbelt, J., Tingey, S. & Mendoza, D. 1996 Mechanisms of gas bubble retention and release: Results for Hanford Waste Tanks 241-S-102 and 241-SY-103 and single-shell tank simulants. Tech. Rep. Pacific Northwest National Lab.CrossRefGoogle Scholar
Glowinski, R., Lions, J.L. & Trémolières, R. 1981 Numerical Analysis of Variational Inequalities. North Holland.Google Scholar
Gonzalez, R., Shaughnessy, J. & Grindle, W. 2000 Industry leaders shed light on drilling riser gas effects. Oil Gas J. 98, 42–43.Google Scholar
Hecht, F. 2012 New development in Freefem++. J. Numer. Maths 20 (3), 251–265.Google Scholar
Hewitt, D.R. & Balmforth, N.J. 2017 Taylor's swimming sheet in a yield-stress fluid. J. Fluid Mech. 828, 33–56.CrossRefGoogle Scholar
Hewitt, D.R. & Balmforth, N.J. 2018 Viscoplastic slender-body theory. J. Fluid Mech. 856, 870–897.CrossRefGoogle Scholar
Hill, R. 1950 The Mathematical Theory of Plasticity. Oxford University Press.Google Scholar
Iglesias, J.A., Mercier, G., Chaparian, E. & Frigaard, I.A. 2020 Computing the yield limit in three-dimensional flows of a yield stress fluid about a settling particle. J. Non-Newtonian Fluid Mech. 284, 104374.CrossRefGoogle Scholar
Johnson, M., Fairweather, M., Harbottle, D., Hunter, T., Peakall, J. & Biggs, S. 2017 Yield stress dependency on the evolution of bubble populations generated in consolidated soft sediments. AIChE J. 63 (9), 3728–3742.CrossRefGoogle Scholar
Johnson, A., Rezmer-Cooper, I., Bailey, T. & McCann, D. 1995 Gas migration: Fast, slow or stopped. Society of Petroleum Engineers paper series (SPE-29342-MS).CrossRefGoogle Scholar
Johnson, A.B. & White, D.B. 1991 Gas-rise velocities during kicks. SPE Drilling Engineering 6 (04), 257–263.CrossRefGoogle Scholar
Karapetsas, G., Photeinos, D., Dimakopoulos, Y. & Tsamopoulos, J. 2019 Dynamics and motion of a gas bubble in a viscoplastic medium under acoustic excitation. J. Fluid Mech. 865, 381–413.CrossRefGoogle Scholar
Liu, Y., Balmforth, N.J., Hormozi, S. & Hewitt, D.R. 2016 Two–dimensional viscoplastic dambreaks. J. Non-Newtonian Fluid Mech. 238, 65–79.CrossRefGoogle Scholar
Lopez, W.F., Naccache, M.F. & de Souza Mendes, P.R. 2018 Rising bubbles in yield stress materials. J. Rheol. 62 (1), 209–219.CrossRefGoogle Scholar
Martin, C.M. & Randolph, M.F. 2006 Upper-bound analysis of lateral pile capacity in cohesive soil. Gèotechnique 56 (2), 141–145.CrossRefGoogle Scholar
Mougin, N., Magnin, A. & Piau, J.M. 2012 The significant influence of internal stresses on the dynamics of bubbles in a yield stress fluid. J. Non-Newtonian Fluid Mech. 171, 42–55.CrossRefGoogle Scholar
Murff, J.D., Wagner, D.A. & Randolph, M.F. 1989 Pipe penetration in cohesive soil. Gèotechnique 39 (2), 213–229.CrossRefGoogle Scholar
Pourzahedi, A., Zare, M. & Frigaard, I.A. 2021 Eliminating injection and memory effects in bubble rise experiments within yield stress fluids. J. Non-Newtonian Fluid Mech. 292, 104531.CrossRefGoogle Scholar
Prager, W. 1954 On slow visco-plastic flow. In Studies in Mathematics and Mechanics, pp. 208–216.Google Scholar
Putz, A. & Frigaard, I.A. 2010 Creeping flow around particles in a Bingham fluid. J. Non-Newtonian Fluid Mech. 165 (5), 263–280.CrossRefGoogle Scholar
Randolph, M.F. & Houlsby, G.T. 1984 The limiting pressure on a circular pile loaded laterally in cohesive soil. Gèotechnique 34 (4), 613–623.CrossRefGoogle Scholar
Roquet, N. & Saramito, P. 2003 An adaptive finite element method for Bingham fluid flows around a cylinder. Comput. Meth. Appl. Mech. Engng 192 (31), 3317–3341.CrossRefGoogle Scholar
Roustaei, A., Chevalier, T., Talon, L. & Frigaard, I.A. 2016 Non-Darcy effects in fracture flows of a yield stress fluid. J. Fluid Mech. 805, 222–261.CrossRefGoogle Scholar
Roustaei, A. & Frigaard, I.A. 2015 Residual drilling mud during conditioning of uneven boreholes in primary cementing. Part 2: steady laminar inertial flows. J. Non-Newtonian Fluid Mech. 226, 1–15.CrossRefGoogle Scholar
Saramito, P. & Roquet, N. 2001 An adaptive finite element method for viscoplastic fluid flows in pipes. Comput. Meth. Appl. Mech. Engng 190 (40–41), 5391–5412.CrossRefGoogle Scholar
Sikorski, D., Tabuteau, H. & de Bruyn, J. 2009 Motion and shape of bubbles rising through a yield-stress fluid. J. Non-Newtonian Fluid Mech. 159 (1–3), 10–16.CrossRefGoogle Scholar
Singh, J.P. & Denn, M. 2008 Interacting two-dimensional bubbles and droplets in a yield-stress fluid. Phys. Fluids 20 (4), 040901.CrossRefGoogle Scholar
Small, C., Cho, S., Hashisho, Z. & Ulrich, A. 2015 Emissions from oil sands tailings ponds: review of tailings pond parameters and emission estimates. J. Petrol. Sci. Engng 127, 490–501.CrossRefGoogle Scholar
Supekar, R., Hewitt, D.R. & Balmforth, N.J. 2020 Translating and squirming cylinders in a viscoplastic fluid. J. Fluid Mech. 882, A11.CrossRefGoogle Scholar
Terasaka, K. & Tsuge, H. 2001 Bubble formation at a nozzle submerged in viscous liquids having yield stress. Chem. Engng Sci. 56 (10), 3237–3245.CrossRefGoogle Scholar
Treskatis, T., Moyers-González, M.A. & Price, C.J. 2016 An accelerated dual proximal gradient method for applications in viscoplasticity. J. Non-Newtonian Fluid Mech. 238, 115–130.CrossRefGoogle Scholar
Treskatis, T., Roustaei, A., Frigaard, I. & Wachs, A. 2018 Practical guidelines for fast, efficient and robust simulations of yield-stress flows without regularisation: a study of accelerated proximal gradient and augmented Lagrangian methods. J. Non-Newtonian Fluid Mech. 262, 149–164.CrossRefGoogle Scholar
Tripathi, M., Sahu, K., Karapetsas, G. & Matar, O. 2015 Bubble rise dynamics in a viscoplastic material. J. Non-Newtonian Fluid Mech. 222, 217–226.CrossRefGoogle Scholar
Tsamopoulos, J., Dimakopoulos, Y., Chatzidai, N., Karapetsas, G. & Pavlidis, M. 2008 Steady bubble rise and deformation in Newtonian and viscoplastic fluids and conditions for bubble entrapment. J. Fluid Mech. 601, 123–164.CrossRefGoogle Scholar
Zare, M., Daneshi, M. & Frigaard, I.A. 2021 Effects of non-uniform rheology on the motion of bubbles in a yield-stress fluid. J. Fluid Mech. 919, A25.CrossRefGoogle Scholar
Zare, M. & Frigaard, I.A. 2018 Onset of miscible and immiscible fluids’ invasion into a viscoplastic fluid. Phys. Fluids 30 (6), 063101.CrossRefGoogle Scholar