Article contents
Flow of a concentrated emulsion with surfactant through a periodic porous medium
Published online by Cambridge University Press: 07 December 2022
Abstract
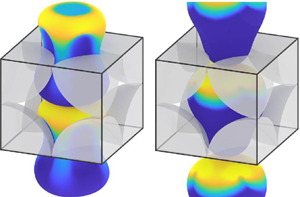
High-resolution, long-time three-dimensional simulations are presented for slow, pressure-driven flow of a periodic emulsion of deformable drops through a dense, simple cubic array of solid spheres (one drop and one particle per periodic cell). The drops, covered with insoluble, non-diffusive surfactant, are large compared with pores, and they squeeze with high resistance, very closely coating the solids to overcome surface tension and lubrication effects. The solid volume fraction is 50 %, the emulsion concentration  $c_{em}$ in the pore space is 36 % or 50 %, the drop-to-medium viscosity ratio
$c_{em}$ in the pore space is 36 % or 50 %, the drop-to-medium viscosity ratio  $\lambda$ is 0.25 to 4. The contamination measure
$\lambda$ is 0.25 to 4. The contamination measure  $\beta \leq 0.1$ keeps the linear surfactant model (assumed in most of the work) physically relevant. The boundary-integral solution requires extreme resolutions (tens of thousands of boundary elements per surface) achieved by multipole acceleration with special desingularizations, combined with flow-biased surfactant transport algorithms for numerical stability. The time-periodic regime is typically attained after a few squeezing cycles; the motion period is used in the extrapolation scheme to evaluate critical capillary numbers
$\beta \leq 0.1$ keeps the linear surfactant model (assumed in most of the work) physically relevant. The boundary-integral solution requires extreme resolutions (tens of thousands of boundary elements per surface) achieved by multipole acceleration with special desingularizations, combined with flow-biased surfactant transport algorithms for numerical stability. The time-periodic regime is typically attained after a few squeezing cycles; the motion period is used in the extrapolation scheme to evaluate critical capillary numbers  $Ca_{crit}$ demarcating squeezing from trapping. Due to Marangoni stresses, even light (
$Ca_{crit}$ demarcating squeezing from trapping. Due to Marangoni stresses, even light ( $\beta =0.05$) to moderate (
$\beta =0.05$) to moderate ( $\beta =0.1$) contaminations significantly reduce the average drop-phase migration velocity (up to 2.8 times, compared with clean drops), especially at small
$\beta =0.1$) contaminations significantly reduce the average drop-phase migration velocity (up to 2.8 times, compared with clean drops), especially at small  $\lambda =0.25$. In contrast,
$\lambda =0.25$. In contrast,  $Ca_{crit}$ is weakly sensitive to contamination and levels off completely at
$Ca_{crit}$ is weakly sensitive to contamination and levels off completely at  $\beta =0.05$. At
$\beta =0.05$. At  $\lambda =0.25$ and
$\lambda =0.25$ and  $c_{em}=0.36$, the average drop-phase velocities are much different for lightly and moderately contaminated emulsions, except for near-critical squeezing when they become the same. Nonlinear surfactant models (Langmuir, Frumkin) are used to validate the linear model.
$c_{em}=0.36$, the average drop-phase velocities are much different for lightly and moderately contaminated emulsions, except for near-critical squeezing when they become the same. Nonlinear surfactant models (Langmuir, Frumkin) are used to validate the linear model.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 1
- Cited by



