Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T23:37:22.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow around six in-line square cylinders

Published online by Cambridge University Press:  03 September 2012

C. M. Sewatkar ,
Rahul Patel ,
Atul Sharma  and
Amit Agrawal
C. M. Sewatkar
Affiliation:
Department of Mechanical Engineering, College of Engineering, Pune 411005, India
Rahul Patel
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
Atul Sharma
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
Amit Agrawal*
Affiliation:
Department of Mechanical Engineering, College of Engineering, Pune 411005, India Department of Mechanical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

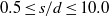The flow around six in-line square cylinders has been studied numerically and experimentally for and 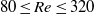, where is the surface-to-surface distance between two cylinders, 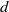is the size of the cylinder and 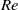is the Reynolds number. The effect of spacing on the flow regimes is initially studied numerically at 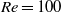for which a synchronous flow regime is observed for 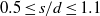, while quasi-periodic-I, quasi-periodic-II and chaotic regimes occur between 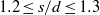, 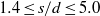and 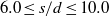, respectively. These regimes have been confirmed via particle-image-velocimetry-based experiments. A flow regime map is proposed as a function of spacing and Reynolds number. The flow is predominantly quasi-periodic-II or chaotic at higher Reynolds numbers. The quasi-periodic and chaotic nature of the flow is due to the wake interference effect of the upstream cylinders which becomes more severe at higher Reynolds numbers. The appearance of flow regimes is opposite to that for a row of cylinders. The Strouhal number for vortex shedding is the same for all the cylinders, especially for synchronous and quasi-periodic-I flow regimes. The mean drag (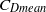) experienced by the cylinders is less than that for an isolated cylinder, irrespective of the spacing. The first cylinder is relatively insensitive to the presence of downstream cylinders and the 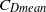is almost constant at 1.2. The 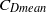for the second and third cylinders may be negative, with the value of 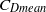increasing monotonically with spacing. The changes in root mean square lift coefficient are consistent with changes in 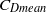. Interestingly, the instantaneous lift force can be larger than the instantaneous drag force on the cylinders. These results should help improve understanding of flow around multiple bluff bodies.

JFM classification

Aerodynamics: Flow-structure interactions Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 195 - 233
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Agrawal, A. & Agrawal, A. 2006 Three-dimensional simulation of gaseous slip flow in different aspect ratio microducts. Phys. Fluids 18, 103604.CrossRefGoogle Scholar
2. Agrawal, A., Djenidi, L. & Antonia, R. A. 2006 Investigation of flow around a pair of side-by-side square cylinders using the lattice Boltzmann method. Comput. Fluids 35, 1093–1107.CrossRefGoogle Scholar
3. Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010a Secondary instability in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.CrossRefGoogle Scholar
4. Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010b Possible states in the flow around two circular cylinders in tandem with separations in the vicinity of the drag inversion spacing. Phys. Fluids 22, 054101.CrossRefGoogle Scholar
5. Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.CrossRefGoogle Scholar
6. Djenidi, L. 2006 Lattice-Boltzmann simulation of grid-generated turbulence. J. Fluid Mech. 552, 13–35.CrossRefGoogle Scholar
7. Frisch, U., Hasslacher, B. & Pomeau, Y. 1986 Lattice-gas automata for the Navier–Stokes equations. Phys. Rev. Lett. 56, 1505–1508.CrossRefGoogle Scholar
8. Harichandan, A. B. & Roy, A. 2010 Numerical investigation of low Reynolds number flow past two and three circular cylinders using unstructured grid CFR scheme. Intl J. Heat Fluid Flow 31, 154–171.CrossRefGoogle Scholar
9. Hetz, A. A., Dhaubhadel, M. N. & Telionis, D. P. 1991 Vortex shedding over five in-line cylinders. J. Fluids Struct. 5, 243–257.CrossRefGoogle Scholar
10. Kim, M. K., Kim, D. K., Yoon, S. H. & Lee, D. H. 2008 Measurements of the flow fields around two square cylinders in tandem arrangement. J. Mech. Sci. Technol. 22, 397–407.CrossRefGoogle Scholar
11. Kumar, S. R., Sharma, A. & Agrawal, A. 2008 Simulation of flow around a row of square cylinders. J. Fluid Mech. 606, 369–397.CrossRefGoogle Scholar
12. Lankadasu, A. & Vengadesan, S. 2007 Interference effect of two equal-sized square cylinders in tandem arrangement: with planar shear flow. Intl J. Numer. Meth. Fluids 57, 1005–1021.CrossRefGoogle Scholar
13. Liang, C., Papadakis, G. & Luo, X. 2009 Effect of tube spacing on the vortex shedding characteristics of laminar flow past an inline tube array: a numerical study. Comput. Fluids 38, 950–964.CrossRefGoogle Scholar
14. Liu, C. H. & Chen, J. M. 2002 Observations of hysteresis in flow around two square cylinders in a tandem arrangement. J. Wind Engng Ind. Aerodyn. 90, 1019–1050.CrossRefGoogle Scholar
15. Luo, S. C. & Teng, T. C. 1990 Aerodynamic forces on a square section cylinder that is downstream to an identical cylinder. Aeronaut. J. 94, 203–212.CrossRefGoogle Scholar
16. Meneghini, J. R., Saltara, F., Siqueira, C. L. R. & Ferrari, J. A. Jr 2001 Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 15, 327–350.CrossRefGoogle Scholar
17. Mittal, S., Kumar, V. & Raghuvanshi, A. 1997 Unsteady incompressible flows past two cylinders in tandem and staggered arrangements. Intl J. Numer. Meth. Fluids 25, 1315–1344.3.0.CO;2-P>CrossRefGoogle Scholar
18. Mizushima, J. & Suehiro, N. 2005 Instability and transition of flow past two tandem circular cylinders. Phys. Fluids 17, 104107.CrossRefGoogle Scholar
19. Saha, A. K., Biswas, G. & Muralidhar, K. 2003 Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Intl J. Heat Fluid Flow 24, 54–66.CrossRefGoogle Scholar
20. Sakemoto, H, Haniu, H. & Obata, Y. 1987 Fluctuating forces acting on two square prisms in a tandem arrangement. J. Wind Engng Ind. Aerodyn. 26, 85–103.CrossRefGoogle Scholar
21. Sewatkar, C. M., Sharma, A. & Agrawal, A. 2009 On the effect of Reynolds number for flow around row of square cylinders. Phys. Fluids 21, 083602.CrossRefGoogle Scholar
22. Sewatkar, C. M., Sharma, A. & Agrawal, A. 2010 A first attempt to numerically compute forces on birds in V formation. Artif. Life 16, 245–258.CrossRefGoogle ScholarPubMed
23. Sewatkar, C. M., Sharma, A. & Agrawal, A. 2011 Simulation of flow across a row of transversely oscillating square cylinders. J. Fluid Mech. 680, 361–397.CrossRefGoogle Scholar
24. Sewatkar, C. M., Sharma, A. & Agrawal, A. 2012 On energy transfer in flow around a row of transversely oscillating square cylinders at low Reynolds number. J. Fluids Struct. 31, 1–17.CrossRefGoogle Scholar
25. Sharma, A. & Eswaran, V. 2004 Heat and fluid flow across a square cylinder in the two-dimensional laminar flow regime. Numer. Heat Transfer A 45, 247–269.CrossRefGoogle Scholar
26. Sohankar, A. & Etminan, A. 2009 Forced convection heat transfer from tandem square cylinders in cross flow at low Reynolds numbers. Intl J. Numer. Meth. Fluids 60, 733–751.CrossRefGoogle Scholar
27. Succi, S. 2001 The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Clarendon.CrossRefGoogle Scholar
28. Sumner, D. 2010 Two circular cylinders in cross-flow: a review. J. Fluids Struct. 26, 849–899.CrossRefGoogle Scholar
29. Wang, S., Tian, F., Jia, L., Lu, X. & Yin, X. 2010 Secondary vortex street in the wake of two tandem circular cylinders at low Reynolds number. Phys. Rev. E 81, 036305.CrossRefGoogle ScholarPubMed
30. Xu, G. & Zhou, Y. 2004 Strouhal numbers in the wake of two in-line cylinders. Exp. Fluids 37, 248–256.CrossRefGoogle Scholar
31. Yen, S. C., San, K. C. & Chuang, T. H. 2008 Interactions of tandem square cylinders at low Reynolds numbers. Expl Fluid Therm. Sci. 32, 927–938.CrossRefGoogle Scholar
32. Zdravkovich, M. M. 1997 Flow around Circular Cylinders: Fundamentals. Oxford University Press.CrossRefGoogle Scholar
33. Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.CrossRefGoogle Scholar