1. Introduction
Understanding the role played by pulsatile or oscillatory flows in the vicinity of deformable walls is crucial in many engineering (Jaffrin & Shapiro Reference Jaffrin and Shapiro1971) and biomedical applications (Grotberg & Jensen Reference Grotberg and Jensen2004). In fact, many of the physiological systems of the human body present this kind of motion. The flow of air in the respiratory system, that of blood in the circulatory system, or the flow of cerebrospinal fluid (CSF) in the central nervous system, constitute relevant examples where the oscillating driving mechanisms, together with the interaction of the fluid with the compliant walls, determine the nature of the fluid motion (Heil & Hazel Reference Heil and Hazel2011; Linninger et al. Reference Linninger, Tangen, Hsu and Frim2016). Nevertheless, despite their relevance, many aspects of oscillatory flow in the presence of compliant walls are still poorly understood. In the present paper we focus on the flow of CSF in the cervical spinal subarachnoid space (SSAS) and its interaction with the fluid in the central canal of the spinal cord through the deformation of the spinal cord tissue that separates both fluid layers (figure 1a). We focus on this configuration in the context of two pathologies, named syringomyelia and hydromyelia. Both conditions are similar and involve the accumulation of fluid in the spinal cord. In syringomyelia it occurs in the form of a slender fluid-filled cavity, called the syrinx, approximately 2–6 cm long and 3–6 mm wide (figure 1b) (Elliott et al. Reference Elliott, Bertram, Martin and Brodbelt2013), whereas in hydromyelia there is an abnormal dilation of the central canal that typically spans a longer section of the spine, approximately 3–4 vertebrae (figure 1c) (Roser et al. Reference Roser, Ebner, Sixt, Hagen and Tatagiba2010). In hydromyelia, the dilated central canal is considered to be connected to the fourth ventricle (which is the case in newborns and young children), whereas in syringomyelia, the cavity may be isolated as a result of age-related obstruction of the central canal. Nevertheless, the distinction between both diseases is often hard to make, and some physicians might even use both terms interchangeably. The pathogenesis of these diseases is still unknown, but there is a consensus that CSF hydrodynamics may play an important role. In fact, many cases of hydromyelia/syringomyelia are associated with a malformation of the hindbrain named ‘type I Chiari malformation’ (CMI), in which the cerebellar tonsils descend into the entrance of the SSAS and partially block the natural oscillatory motion of CSF (figure 1b). This back-and-forth motion of CSF in the SSAS surrounding the spinal cord is in principle coupled to the motion of fluid in the central canal, with associated periodic deformations of the compliant spinal cord tissue. Whereas in healthy subjects these deformations may remain small, in subjects with Chiari malformation the changed hydrodynamics in the subarachnoid space may induce larger self-sustained deformations of the spinal cord tissue separating the two fluid layers. Prolonged exposure to such deformations may then in turn be associated with additional oedema or fluid transport into the fluid cavity, leading to the growth of cavities, whose size may be marked by the wavelength of the preferential deformations. As a first step to explore if this proposed mechanism is viable, in the present paper we study the underlying fluid–structure interaction problem using a simplified model description.

Figure 1. (a) Schematic overview of the main features of the anatomy of the cervical spine. (b) Schematic representation of syringomyelia associated with type I Chiari malformation. (c) Schematic representation of hydromyelia. (d) Diagram and photograph (Cloyd & Low Reference Cloyd and Low1974) of the microanatomy inside the SSAS: AM, arachnoid mater; AT, arachnoid trabeculae; A, artery; SAS, subarachnoid space; DM, dura mater; PM, pia mater; SPC, spinal cord.
The main features of the anatomy of the cervical spine that are relevant to the problem at hand are given in figure 1. The SSAS is a thin annular canal, approximately ![]() $H^\ast_{SSAS} \sim 1\unicode{x2013}4\ \text {mm}$ wide, bounded internally by the pia membrane (thickness
$H^\ast_{SSAS} \sim 1\unicode{x2013}4\ \text {mm}$ wide, bounded internally by the pia membrane (thickness ![]() $t^\ast _{pia} \sim 100 \, \mathrm {\mu }\text {m}$) and externally by the dura membrane. At the centre of the spinal cord lies the central canal, which in healthy subjects has a cross-sectional diameter of approximately 0.5–2 mm. In the presence of hydromyelia/syringomyelia its diameter increases to approximately 3–4 mm. The CSF is a water-like fluid with a density
$t^\ast _{pia} \sim 100 \, \mathrm {\mu }\text {m}$) and externally by the dura membrane. At the centre of the spinal cord lies the central canal, which in healthy subjects has a cross-sectional diameter of approximately 0.5–2 mm. In the presence of hydromyelia/syringomyelia its diameter increases to approximately 3–4 mm. The CSF is a water-like fluid with a density ![]() $\rho _{CSF} \simeq 1000\ \text {kg}\ \text {m}^{-3}$ and a kinematic viscosity
$\rho _{CSF} \simeq 1000\ \text {kg}\ \text {m}^{-3}$ and a kinematic viscosity ![]() $\nu _{CSF} \simeq 0.7\times 10^{-6}\ \text {m}^2\ \text {s}^{-1}$. Its motion in the subarachnoid space is driven mainly by the intracranial pressure fluctuations that occur with each heartbeat as a result of the cyclic variation of the cerebrovascular blood volume (with frequencies of the order of
$\nu _{CSF} \simeq 0.7\times 10^{-6}\ \text {m}^2\ \text {s}^{-1}$. Its motion in the subarachnoid space is driven mainly by the intracranial pressure fluctuations that occur with each heartbeat as a result of the cyclic variation of the cerebrovascular blood volume (with frequencies of the order of ![]() $\omega ^{\ast }_{CSF}/(2{\rm \pi} ) \sim 1\ \text {Hz}$), resulting in a volume of CSF of approximately
$\omega ^{\ast }_{CSF}/(2{\rm \pi} ) \sim 1\ \text {Hz}$), resulting in a volume of CSF of approximately ![]() $1\ \text {ml}$ that is cyclically pushed into and out of the spinal canal, as measured in multiple studies using magnetic resonance imaging (see, for example, Coenen et al. (Reference Coenen, Gutiérrez-Montes, Sincomb, Criado-Hidalgo, Wei, King, Haughton, Martínez-Bazán, Sánchez and Lasheras2019) and Sincomb et al. (Reference Sincomb, Coenen, Gutiérrez-Montes, Bazán, Haughton and Sánchez2022)). The back-and-forth motion of CSF has a typical stroke length
$1\ \text {ml}$ that is cyclically pushed into and out of the spinal canal, as measured in multiple studies using magnetic resonance imaging (see, for example, Coenen et al. (Reference Coenen, Gutiérrez-Montes, Sincomb, Criado-Hidalgo, Wei, King, Haughton, Martínez-Bazán, Sánchez and Lasheras2019) and Sincomb et al. (Reference Sincomb, Coenen, Gutiérrez-Montes, Bazán, Haughton and Sánchez2022)). The back-and-forth motion of CSF has a typical stroke length ![]() $l^\ast _{CSF} \sim 5\unicode{x2013}10\ \text {mm}$, and a characteristic velocity
$l^\ast _{CSF} \sim 5\unicode{x2013}10\ \text {mm}$, and a characteristic velocity ![]() $U^\ast _{CSF} \sim 1\unicode{x2013}2 \ \text {cm}\ \text {s}^{-1}$. The corresponding instantaneous Reynolds number is therefore of the order of
$U^\ast _{CSF} \sim 1\unicode{x2013}2 \ \text {cm}\ \text {s}^{-1}$. The corresponding instantaneous Reynolds number is therefore of the order of ![]() $U^\ast _{CSF} H^\ast_{SSAS} / \nu _{CSF} \sim 50$, and the corresponding Womersley number is of the order of
$U^\ast _{CSF} H^\ast_{SSAS} / \nu _{CSF} \sim 50$, and the corresponding Womersley number is of the order of ![]() $H^\ast_{SSAS}\sqrt {\omega ^\ast _{CSF}/\nu _{CSF}} \sim 8$. Note that in the model problem to be presented below we will base the Reynolds number on the stroke length, so that its corresponding order of magnitude is
$H^\ast_{SSAS}\sqrt {\omega ^\ast _{CSF}/\nu _{CSF}} \sim 8$. Note that in the model problem to be presented below we will base the Reynolds number on the stroke length, so that its corresponding order of magnitude is ![]() $U^\ast _{CSF} l^\ast _{CSF} / \nu _{CSF} \sim 150$. When the central canal is connected to the fourth ventricle, which is in turn connected with the subarachnoid space, both fluid layers are subject to the same instantaneous pressure. The longitudinal pressure gradient is therefore dictated by the pressure at the caudal end of the layers. Despite there not being a direct connection between the central canal and the spinal subarachnoid space at the caudal end of the spinal cord, it is plausible to assume that the pressures on both sides of the spinal cord tissue are approximately equal. The contrary would lead to deformations, which are not observed in clinical reports of healthy subjects. Velocity measurements inside the central canal of healthy subjects are not available in the literature because the diameter of the canal is too small for current MRI techniques. Nevertheless, there are a few measurements of flow inside large syringomyelia cysts, showing oscillatory motion in sync with that of CSF in the subarachnoid space surrounding the spinal cord (for example Honey, Martin & Heran (Reference Honey, Martin and Heran2017) and Luzzi et al. (Reference Luzzi, Lucifero, Elsawaf, Elbabaa, Del Maestro, Savioli, Galzio and Gragnaniello2021)). Various microanatomical features, such as nerve roots, denticulate ligaments and trabeculae connect the pia membrane around the spinal cord with the outer dura mater. Among these, the trabeculae (figure 1d) are especially relevant for the present problem, since they constitute a network of pillar-like structures that maintain the spinal cord in its position inside the spinal canal and in this manner give stiffness to the otherwise relatively flexible spinal cord tissue. The diameters of the trabeculae are of the order of
$U^\ast _{CSF} l^\ast _{CSF} / \nu _{CSF} \sim 150$. When the central canal is connected to the fourth ventricle, which is in turn connected with the subarachnoid space, both fluid layers are subject to the same instantaneous pressure. The longitudinal pressure gradient is therefore dictated by the pressure at the caudal end of the layers. Despite there not being a direct connection between the central canal and the spinal subarachnoid space at the caudal end of the spinal cord, it is plausible to assume that the pressures on both sides of the spinal cord tissue are approximately equal. The contrary would lead to deformations, which are not observed in clinical reports of healthy subjects. Velocity measurements inside the central canal of healthy subjects are not available in the literature because the diameter of the canal is too small for current MRI techniques. Nevertheless, there are a few measurements of flow inside large syringomyelia cysts, showing oscillatory motion in sync with that of CSF in the subarachnoid space surrounding the spinal cord (for example Honey, Martin & Heran (Reference Honey, Martin and Heran2017) and Luzzi et al. (Reference Luzzi, Lucifero, Elsawaf, Elbabaa, Del Maestro, Savioli, Galzio and Gragnaniello2021)). Various microanatomical features, such as nerve roots, denticulate ligaments and trabeculae connect the pia membrane around the spinal cord with the outer dura mater. Among these, the trabeculae (figure 1d) are especially relevant for the present problem, since they constitute a network of pillar-like structures that maintain the spinal cord in its position inside the spinal canal and in this manner give stiffness to the otherwise relatively flexible spinal cord tissue. The diameters of the trabeculae are of the order of ![]() $d^\ast _{trab} \sim 10\unicode{x2013}20\,\mathrm {\mu }\text {m}$, and they are spaced approximately
$d^\ast _{trab} \sim 10\unicode{x2013}20\,\mathrm {\mu }\text {m}$, and they are spaced approximately ![]() $s^\ast _{trab} \sim 500\,\mathrm {\mu }\text {m}$ apart (Stockman Reference Stockman2006; Gupta et al. Reference Gupta, Soellinger, Boesiger, Poulikakos and Kurtcuoglu2009; Salerno, Cardillo & Camporeale Reference Salerno, Cardillo and Camporeale2020). In the problem formulation (§ 2.1), we will show with an order of magnitude estimation of the governing fluid–structure interaction equation that the stiffness provided by the trabeculae is indeed the dominating effect that balances the normal force exerted by the two fluid layers on the separating spinal cord.
$s^\ast _{trab} \sim 500\,\mathrm {\mu }\text {m}$ apart (Stockman Reference Stockman2006; Gupta et al. Reference Gupta, Soellinger, Boesiger, Poulikakos and Kurtcuoglu2009; Salerno, Cardillo & Camporeale Reference Salerno, Cardillo and Camporeale2020). In the problem formulation (§ 2.1), we will show with an order of magnitude estimation of the governing fluid–structure interaction equation that the stiffness provided by the trabeculae is indeed the dominating effect that balances the normal force exerted by the two fluid layers on the separating spinal cord.
Inspired by the complex biofluid mechanical problem described in the previous paragraph, in the present paper we study a simplified, canonical configuration, consisting of two infinitely long layers of fluid that undergo an oscillatory motion parallel to a thin planar flexible wall that separates them. We investigate whether the separating wall will remain undeformed, the two oscillatory Stokes layers that form on both sides remaining unperturbed, or whether the configuration acquires a different oscillatory state in which the wall moves together with the two layers. We aim to answer this question by means of a Floquet linear stability analysis, exploring the influence of the different governing parameters such as the layer widths, the Reynolds number and the wall stiffness. The study of fluid–structure interactions in simplified two-layer oscillating flow configurations such as the one presented here may prove helpful to elucidate some of the mechanisms that intervene in the complex, real-life flow described earlier.
The literature on the stability of time-periodic flows in the presence of compliant walls is limited. On the contrary, its rigid counterpart has been studied extensively (Davis Reference Davis1976). The stability of the planar Stokes layer near a rigid wall was investigated by Hall (Reference Hall1978) and Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002). Time-periodic channel and pipe flows with rigid walls have been studied by Yang & Yih (Reference Yang and Yih1977), von Kerczek (Reference von Kerczek1982), Thomas et al. (Reference Thomas, Bassom, Blennerhassett and Davies2011), Pier & Schmid (Reference Pier and Schmid2017) and Pier & Schmid (Reference Pier and Schmid2021), using linear Floquet analyses, non-modal stability analyses, as well fully nonlinear direct numerical simulations. Nevertheless, the absence of flexible walls limits the implications of their findings for the problem under consideration here. The hydrodynamic stability of flows near flexible walls has been mainly focused on steady configurations. Canonical examples include the Couette flow past a flexible membrane (Kumaran & Srivatsan Reference Kumaran and Srivatsan1998; Thaokar & Kumaran Reference Thaokar and Kumaran2002; Kumaran Reference Kumaran2021), and the Poiseuille flow between compliant walls (Carpenter & Garrad Reference Carpenter and Garrad1985; Davies & Carpenter Reference Davies and Carpenter1997; Lebbal, Alizard & Pier Reference Lebbal, Alizard and Pier2022b). The coupling between the wall displacement and fluid velocity provides additional destabilizing mechanisms that enrich the stability characteristics drastically with respect to the rigid analogues of these flows. To the best of our knowledge, there are only a few studies in the literature on the stability of flows that contain both time-periodicity and flexible walls, among which the most relevant for the problem at hand work are the stability analyses of plane pulsatile channel flow between compliant walls by Tsigklifis & Lucey (Reference Tsigklifis and Lucey2017) and Lebbal, Alizard & Pier (Reference Lebbal, Alizard and Pier2022a), and the study of oscillating flow in a channel between a flexible wall and a rigid wall undergoing an in-plane pulsating motion by Thaokar & Kumaran (Reference Thaokar and Kumaran2004). Nevertheless, the main focus of these works is on the stabilizing or destabilizing influence of the modulation of the high-Reynolds-number mean flow, in contrast to the present work, in which the time-average of the basic oscillatory motion is zero.
The remainder of the paper is organized as follows. In § 2, we describe the problem configuration, derive the basic oscillatory flow and apply the Floquet formalism to the Navier–Stokes equations in combination with a simple model equation for the fluid–wall interactions to derive a set of stability equations that is to be solved numerically. The computational method employed to achieve this is set out in § 3. The results are described in detail in § 4. In particular, we focus on the marginal conditions for the onset of instability, investigating the influence of the perturbation wavelength and the control parameters of the problem, which are the layer widths, the Reynolds number and the wall stiffness. Finally, concluding remarks are given in § 5.
2. Problem formulation
2.1. Governing equations and scaling
Based on the description of cerebrospinal fluid flow in the cervical spine given in § 1, we consider here a simplified model problem that consists of an infinitely long channel of fluid with constant density ![]() $\rho$ and kinematic viscosity
$\rho$ and kinematic viscosity ![]() $\nu$, divided longitudinally into two layers of widths
$\nu$, divided longitudinally into two layers of widths ![]() $H^\ast_1$ and
$H^\ast_1$ and ![]() $H^\ast_2$ by an infinitesimally thin flexible wall, as depicted in figure 2. Both layers are subject to the same oscillatory pressure gradient in the longitudinal
$H^\ast_2$ by an infinitesimally thin flexible wall, as depicted in figure 2. Both layers are subject to the same oscillatory pressure gradient in the longitudinal ![]() ${x^\ast }$ direction,
${x^\ast }$ direction, ![]() $-{{\partial {{p^\ast }}}/{\partial {{x^\ast }}}} = {\varPi _\ell ^\ast } \cos ({\omega ^\ast } {t^\ast })$ where
$-{{\partial {{p^\ast }}}/{\partial {{x^\ast }}}} = {\varPi _\ell ^\ast } \cos ({\omega ^\ast } {t^\ast })$ where ![]() $\omega ^*$ denotes the angular frequency, which drives an oscillatory flow parallel to the walls and
$\omega ^*$ denotes the angular frequency, which drives an oscillatory flow parallel to the walls and ![]() ${\varPi _\ell ^\ast }$ is the amplitude of the pressure gradient. In the present analysis we are concerned with the stability of the basic oscillatory state in which the separating wall remains undeformed, and the motion in the two layers reduces to the unidirectional planar Womersley flow (see § 2.2). In the unstable regime, the separating wall undergoes deformations that are coupled to the fluid flow.
${\varPi _\ell ^\ast }$ is the amplitude of the pressure gradient. In the present analysis we are concerned with the stability of the basic oscillatory state in which the separating wall remains undeformed, and the motion in the two layers reduces to the unidirectional planar Womersley flow (see § 2.2). In the unstable regime, the separating wall undergoes deformations that are coupled to the fluid flow.
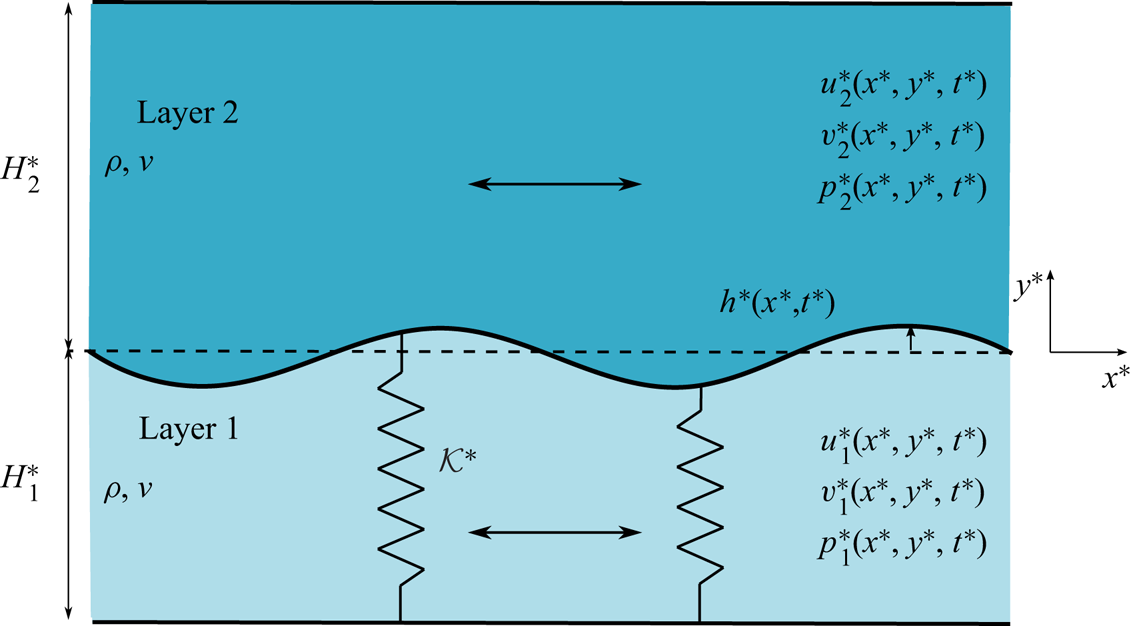
Figure 2. Schematic representation of the flow configuration.
The choice of the particular fluid–structure interaction model considered here, i.e. a massless undamped spring-backed plate, is motivated by the cerebrospinal fluid flow on both sides of the spinal cord, the springs mimicking the trabeculae that keep the spinal cord in place within the spinal canal (figure 1d). The general form of the spring-backed plate-membrane equation, under the assumption of negligible tangential forces on the wall, and constraining the wall motion to the transverse ![]() $y$ direction, takes on the form (see for example Carpenter & Garrad (Reference Carpenter and Garrad1985), Davies & Carpenter (Reference Davies and Carpenter1997) or Shankar & Kumaran (Reference Shankar and Kumaran2002))
$y$ direction, takes on the form (see for example Carpenter & Garrad (Reference Carpenter and Garrad1985), Davies & Carpenter (Reference Davies and Carpenter1997) or Shankar & Kumaran (Reference Shankar and Kumaran2002))
where ![]() ${h^\ast }({x^\ast }, {t^\ast })$ is the transverse plate displacement, and
${h^\ast }({x^\ast }, {t^\ast })$ is the transverse plate displacement, and ![]() $[{p^\ast }]_2^1$ is the pressure difference between the two sides of the membrane in the
$[{p^\ast }]_2^1$ is the pressure difference between the two sides of the membrane in the ![]() ${y^\ast }$ direction. In the model,
${y^\ast }$ direction. In the model, ![]() $m^\ast$ is the membrane mass per unit of area,
$m^\ast$ is the membrane mass per unit of area, ![]() $d^\ast$ is the wall-damping coefficient,
$d^\ast$ is the wall-damping coefficient, ![]() $B^\ast$ is the flexural rigidity,
$B^\ast$ is the flexural rigidity, ![]() $T^\ast$ is the longitudinal tension per unit width and
$T^\ast$ is the longitudinal tension per unit width and ![]() ${\mathcal {K}^\ast }$ is the spring stiffness associated with the trabeculae. Taking into account that the spring stiffness of a single trabecular structure is of the order of
${\mathcal {K}^\ast }$ is the spring stiffness associated with the trabeculae. Taking into account that the spring stiffness of a single trabecular structure is of the order of ![]() $E_{trab} d^{\ast 2}_{trab}/H^\ast_{SSAS}$, and that there are of the order of
$E_{trab} d^{\ast 2}_{trab}/H^\ast_{SSAS}$, and that there are of the order of ![]() $1/s^{\ast 2}_{trab}$ trabeculae per unit area, the spring stiffness coefficient
$1/s^{\ast 2}_{trab}$ trabeculae per unit area, the spring stiffness coefficient ![]() ${\mathcal {K}^\ast }$ in (2.1) can be estimated to be
${\mathcal {K}^\ast }$ in (2.1) can be estimated to be
Here ![]() $E_{trab} \sim 12\ \text {kPa}$ is the trabecular Young's modulus (Jin, Yang & King Reference Jin, Yang and King2011),
$E_{trab} \sim 12\ \text {kPa}$ is the trabecular Young's modulus (Jin, Yang & King Reference Jin, Yang and King2011), ![]() $d^{\ast }_{trab} \sim 10\unicode{x2013}20\,\mathrm {\mu }\text {m}$ the typical diameter of the trabeculae,
$d^{\ast }_{trab} \sim 10\unicode{x2013}20\,\mathrm {\mu }\text {m}$ the typical diameter of the trabeculae, ![]() $H^\ast _{SSAS} \sim 1\unicode{x2013}4\ \text {mm}$ the width of the spinal canal (in other words, the length of the trabeculae) and
$H^\ast _{SSAS} \sim 1\unicode{x2013}4\ \text {mm}$ the width of the spinal canal (in other words, the length of the trabeculae) and ![]() $s^\ast _{trab} \sim 500\,\mathrm {\mu }\text {m}$ the mean distance between trabeculae (figure 1d).
$s^\ast _{trab} \sim 500\,\mathrm {\mu }\text {m}$ the mean distance between trabeculae (figure 1d).
Let us now compare the order of magnitude of the other terms on the left-hand side of (2.1) with that of the spring-stiffness term, ![]() ${\mathcal {K}^\ast }{h^\ast }$. In these estimations, in addition to the aforementioned properties of the trabeculae, we need the Young's modulus and Poisson ratio of the pia mater,
${\mathcal {K}^\ast }{h^\ast }$. In these estimations, in addition to the aforementioned properties of the trabeculae, we need the Young's modulus and Poisson ratio of the pia mater, ![]() $E_{pia} \sim 15\ \text {kPa}$ and
$E_{pia} \sim 15\ \text {kPa}$ and ![]() $\nu _s \sim 0.5$, and its characteristic thickness,
$\nu _s \sim 0.5$, and its characteristic thickness, ![]() $t^\ast _{pia} \sim 100\,\mathrm {\mu }\text {m}$. We also assume small deformations in the transverse direction, of the order of
$t^\ast _{pia} \sim 100\,\mathrm {\mu }\text {m}$. We also assume small deformations in the transverse direction, of the order of ![]() $h^\ast _c \sim t^\ast _{PIA}$, that span a longitudinal distance comparable to the stroke length of the cervical CSF motion,
$h^\ast _c \sim t^\ast _{PIA}$, that span a longitudinal distance comparable to the stroke length of the cervical CSF motion, ![]() $l^\ast _{CSF} \sim 1\ \text {cm}$ (Carpenter & Garrad Reference Carpenter and Garrad1985; Howell, Kozyreff & Ockendon Reference Howell, Kozyreff and Ockendon2008). The relative orders of magnitude of inertia, flexural rigidity and longitudinal tension with respect to the string stiffness are, respectively,
$l^\ast _{CSF} \sim 1\ \text {cm}$ (Carpenter & Garrad Reference Carpenter and Garrad1985; Howell, Kozyreff & Ockendon Reference Howell, Kozyreff and Ockendon2008). The relative orders of magnitude of inertia, flexural rigidity and longitudinal tension with respect to the string stiffness are, respectively,
 $$\begin{gather} \frac{O\left(m^\ast \dfrac{\partial^2 {h^\ast}}{\partial {t^\ast}^2}\right)}{O\left({\mathcal{K}^\ast}{h^\ast}\right)} \sim \frac{\rho_{pia}t^\ast_{pia}{\omega^\ast}^2}{E_{trab}d^{{\ast} 2}_{trab}/H^\ast_{SSAS}s^{{\ast} 2}_{trab}} \sim 10^{{-}3}, \end{gather}$$
$$\begin{gather} \frac{O\left(m^\ast \dfrac{\partial^2 {h^\ast}}{\partial {t^\ast}^2}\right)}{O\left({\mathcal{K}^\ast}{h^\ast}\right)} \sim \frac{\rho_{pia}t^\ast_{pia}{\omega^\ast}^2}{E_{trab}d^{{\ast} 2}_{trab}/H^\ast_{SSAS}s^{{\ast} 2}_{trab}} \sim 10^{{-}3}, \end{gather}$$ $$\begin{gather}\frac{O\left(B^\ast \dfrac{\partial^4 {h^\ast}}{\partial {x^\ast}^4}\right)}{O\left({\mathcal{K}^\ast}{h^\ast}\right)} \sim \frac{E_{pia}t^{{\ast} 3}_{pia}/12(1-\nu_s^2) \, l^{{\ast} 4}_{CSF}}{E_{trab}d^{{\ast} 2}_{trab}/H^\ast_{SSAS}s^{{\ast} 2}_{trab}} \sim 10^{{-}5}, \end{gather}$$
$$\begin{gather}\frac{O\left(B^\ast \dfrac{\partial^4 {h^\ast}}{\partial {x^\ast}^4}\right)}{O\left({\mathcal{K}^\ast}{h^\ast}\right)} \sim \frac{E_{pia}t^{{\ast} 3}_{pia}/12(1-\nu_s^2) \, l^{{\ast} 4}_{CSF}}{E_{trab}d^{{\ast} 2}_{trab}/H^\ast_{SSAS}s^{{\ast} 2}_{trab}} \sim 10^{{-}5}, \end{gather}$$ $$\begin{gather}\frac{O\left(T^\ast \dfrac{\partial^2 {h^\ast}}{\partial {x^\ast}^2}\right)}{O\left({\mathcal{K}^\ast}{h^\ast}\right)} \sim \frac{E_{pia}t^\ast_{pia} h^{{\ast} 2}_{c}/(1-\nu_s^2)\, l^{{\ast} 4}_{CSF}}{E_{trab}d^{{\ast} 2}_{trab}/H^\ast_{SSAS}\, s^{{\ast} 2}_{trab}} \sim 10^{{-}4}. \end{gather}$$
$$\begin{gather}\frac{O\left(T^\ast \dfrac{\partial^2 {h^\ast}}{\partial {x^\ast}^2}\right)}{O\left({\mathcal{K}^\ast}{h^\ast}\right)} \sim \frac{E_{pia}t^\ast_{pia} h^{{\ast} 2}_{c}/(1-\nu_s^2)\, l^{{\ast} 4}_{CSF}}{E_{trab}d^{{\ast} 2}_{trab}/H^\ast_{SSAS}\, s^{{\ast} 2}_{trab}} \sim 10^{{-}4}. \end{gather}$$ Damping is also considered to be negligible compared with the spring stiffness, with ![]() $d^{\ast }{\omega ^\ast }/{\mathcal {K}^\ast } \sim 10^{-2}$ (Fiford & Bilston Reference Fiford and Bilston2005). (The reader is referred to § 4.3 where we briefly explore the effect of the addition of this term, which only introduces little variations in the Floquet growth rate
$d^{\ast }{\omega ^\ast }/{\mathcal {K}^\ast } \sim 10^{-2}$ (Fiford & Bilston Reference Fiford and Bilston2005). (The reader is referred to § 4.3 where we briefly explore the effect of the addition of this term, which only introduces little variations in the Floquet growth rate ![]() $|\mu |$ and the critical Reynolds number
$|\mu |$ and the critical Reynolds number ![]() ${ {Re}}_{cr}$ without changing the most unstable wavelength.) It follows that in the fluid–structure interaction model (2.1), the spring stiffness is the dominating term on the left-hand side that needs to balance the pressure difference between both sides of the wall induced by the fluid motion. Consequently, we focus our attention on the simplified model with
${ {Re}}_{cr}$ without changing the most unstable wavelength.) It follows that in the fluid–structure interaction model (2.1), the spring stiffness is the dominating term on the left-hand side that needs to balance the pressure difference between both sides of the wall induced by the fluid motion. Consequently, we focus our attention on the simplified model with ![]() $m^\ast = d^\ast = B^\ast = T^\ast = 0$, given by
$m^\ast = d^\ast = B^\ast = T^\ast = 0$, given by
Note that this choice of fluid–wall coupling has been adopted in many biofluid mechanical problems in the literature (Čanić et al. Reference Čanić, Tambača, Guidoboni, Mikelić, Hartley and Rosenstrauch2006; Westerhof, Lankhaar & Westerhof Reference Westerhof, Lankhaar and Westerhof2009; Sánchez et al. Reference Sánchez, Martínez-Bazán, Gutiérrez-Montes, Criado-Hidalgo, Pawlak, Bradley, Haughton and Lasheras2018).
When considering the fluid motion, it can be anticipated that in the regime of interest, i.e. near the critical conditions for the onset of instability, the thickness of the Stokes shear-wave layers near the walls is of the same order of magnitude or smaller than the channel half-widths, ![]() $\sqrt {\nu /{\omega ^\ast }} \lesssim H^\ast_{1,2}$, while the characteristic oscillatory velocity in the bulk of the fluid layers is
$\sqrt {\nu /{\omega ^\ast }} \lesssim H^\ast_{1,2}$, while the characteristic oscillatory velocity in the bulk of the fluid layers is ![]() ${U^\ast } \sim {\varPi _\ell ^\ast }/(\rho {\omega ^\ast })$, given by the balance between the driving pressure gradient and the local acceleration. Correspondingly, the typical length scale is the stroke length
${U^\ast } \sim {\varPi _\ell ^\ast }/(\rho {\omega ^\ast })$, given by the balance between the driving pressure gradient and the local acceleration. Correspondingly, the typical length scale is the stroke length ![]() $l^{\ast } \sim {U^\ast }{\omega ^\ast }^{-1}$. Scaling lengths with
$l^{\ast } \sim {U^\ast }{\omega ^\ast }^{-1}$. Scaling lengths with ![]() $l^{\ast }$, time with
$l^{\ast }$, time with ![]() ${\omega ^\ast }^{-1}$, velocities with
${\omega ^\ast }^{-1}$, velocities with ![]() ${U^\ast }$ and pressures with
${U^\ast }$ and pressures with ![]() ${\varPi _\ell ^\ast }^2/(\rho {\omega ^\ast }^2)$, the dimensionless governing equations become (with the subindex
${\varPi _\ell ^\ast }^2/(\rho {\omega ^\ast }^2)$, the dimensionless governing equations become (with the subindex ![]() $j = 1,2$ distinguishing between layer 1,
$j = 1,2$ distinguishing between layer 1, ![]() $y < 0$, and layer 2,
$y < 0$, and layer 2, ![]() $y \geq 0$)
$y \geq 0$)
The Reynolds number ![]() ${ {Re}} = {U^\ast }^2/(\nu {\omega ^\ast }) = {U^\ast } l^{\ast } / \nu = {\varPi _\ell ^\ast }^2/(\rho ^2\nu {\omega ^\ast }^3)$ and thedimensionless wall stiffness
${ {Re}} = {U^\ast }^2/(\nu {\omega ^\ast }) = {U^\ast } l^{\ast } / \nu = {\varPi _\ell ^\ast }^2/(\rho ^2\nu {\omega ^\ast }^3)$ and thedimensionless wall stiffness ![]() $\mathcal {K} = {\mathcal {K}^\ast }/{\varPi _\ell ^\ast } = {\mathcal {K}^\ast }/(\rho {U^\ast } {\omega ^\ast })$ are the parameters that, together with the dimensionless channel widths
$\mathcal {K} = {\mathcal {K}^\ast }/{\varPi _\ell ^\ast } = {\mathcal {K}^\ast }/(\rho {U^\ast } {\omega ^\ast })$ are the parameters that, together with the dimensionless channel widths ![]() $H_1 = H^\ast_1/l^{\ast }$ and
$H_1 = H^\ast_1/l^{\ast }$ and ![]() $H_2 = H^\ast_2/l^{\ast }$, govern the problem. Note that for the flow of CSF near the spinal cord suspended by the trabecular network inside the subarachnoid space,
$H_2 = H^\ast_2/l^{\ast }$, govern the problem. Note that for the flow of CSF near the spinal cord suspended by the trabecular network inside the subarachnoid space, ![]() $\mathcal {K} \sim 2\unicode{x2013}4$, as can be obtained by introducing the values of the geometric and elastic parameters of the problem in (2.2). In § 4 we will see that the fluid–structure interaction is indeed found to be optimal for order unity values of
$\mathcal {K} \sim 2\unicode{x2013}4$, as can be obtained by introducing the values of the geometric and elastic parameters of the problem in (2.2). In § 4 we will see that the fluid–structure interaction is indeed found to be optimal for order unity values of ![]() $\mathcal {K}$.
$\mathcal {K}$.
The boundary conditions to be satisfied are the non-slip conditions at the channel walls and the kinematic condition at the deformable separating boundary,
 \begin{equation} \left. \begin{array}{ll@{}} y = H_2: & u_2 = 0, v_2 = 0,\\ y = h: & u_1 = u_2 = 0, v_1 = v_2 = {{\partial{h}}/{\partial{t}}},\\ y ={-}H_1: & u_1 = 0, v_1 = 0. \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{ll@{}} y = H_2: & u_2 = 0, v_2 = 0,\\ y = h: & u_1 = u_2 = 0, v_1 = v_2 = {{\partial{h}}/{\partial{t}}},\\ y ={-}H_1: & u_1 = 0, v_1 = 0. \end{array} \right\} \end{equation}
Note that when ![]() $H_1, H_2$ become very large compared with the Stokes layer thickness, of order
$H_1, H_2$ become very large compared with the Stokes layer thickness, of order ![]() $1/\sqrt {{ {Re}}}$, the velocity profiles outside the Stokes layers tend to be uniform
$1/\sqrt {{ {Re}}}$, the velocity profiles outside the Stokes layers tend to be uniform ![]() $(\sin t, 0)$. In those cases, the Stokes layer on the non-deformable wall is so far away that it does not influence the flow near the flexible wall any longer. In the present work we focus on Reynolds numbers of order unity or larger, so that the thickness of the Stokes layer is order unity or smaller. Therefore, a pragmatic approach to study the case
$(\sin t, 0)$. In those cases, the Stokes layer on the non-deformable wall is so far away that it does not influence the flow near the flexible wall any longer. In the present work we focus on Reynolds numbers of order unity or larger, so that the thickness of the Stokes layer is order unity or smaller. Therefore, a pragmatic approach to study the case ![]() $H_1, H_2 \to \infty$ is to substitute the boundary conditions (2.11) by
$H_1, H_2 \to \infty$ is to substitute the boundary conditions (2.11) by
 \begin{equation} \left. \begin{array}{ll@{}} y \to \infty: & u_2 \to \sin t, v_2 = 0,\\ y = h: & u_1 = u_2 = 0, v_1 = v_2 = {{\partial{h}}/{\partial{t}}},\\ y \to -\infty: & u_1 \to \sin t, v_1 = 0. \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{ll@{}} y \to \infty: & u_2 \to \sin t, v_2 = 0,\\ y = h: & u_1 = u_2 = 0, v_1 = v_2 = {{\partial{h}}/{\partial{t}}},\\ y \to -\infty: & u_1 \to \sin t, v_1 = 0. \end{array} \right\} \end{equation}2.2. Oscillatory base flow
The basic state about which the Floquet stability analysis is performed is the strictly parallel Womersley-like flow driven by the oscillatory pressure gradient when the separating boundary remains undeformed, given by
with ![]() $\beta = (1+\mathrm {i}) \sqrt {{ {Re}}/2}$. Notice that, since the tangential stresses are not taken into account, the base flow of both streams must be in phase for the separating surface to remain undeformed. In the limit
$\beta = (1+\mathrm {i}) \sqrt {{ {Re}}/2}$. Notice that, since the tangential stresses are not taken into account, the base flow of both streams must be in phase for the separating surface to remain undeformed. In the limit ![]() $H_1,H_2\to \infty$, the basic state becomes
$H_1,H_2\to \infty$, the basic state becomes
As an example, figure 3 shows the base flow for three different combinations of ![]() $H_1$,
$H_1$, ![]() $H_2$ and
$H_2$ and ![]() ${ {Re}}$.
${ {Re}}$.

Figure 3. Oscillatory base flow at four instants of time during an oscillation cycle, for (a) ![]() $H_1, H_2 \to \infty$ and
$H_1, H_2 \to \infty$ and ![]() ${ {Re}} = 21.3$; (b)
${ {Re}} = 21.3$; (b) ![]() $H_1 = 3$,
$H_1 = 3$, ![]() $H_2 = 4$ and
$H_2 = 4$ and ![]() ${ {Re}} = 27.2$; and (c)
${ {Re}} = 27.2$; and (c) ![]() $H_1 = 1$,
$H_1 = 1$, ![]() $H_2 = 2$ and
$H_2 = 2$ and ![]() ${ {Re}} = 60.1$.
${ {Re}} = 60.1$.
2.3. Floquet linear stability analysis
Floquet theory (Iooss & Joseph Reference Iooss and Joseph2012) is employed to analyse the stability of the basic oscillatory state. To that aim, small perturbations in the form of space-periodic Floquet modes are superposed onto the basic oscillatory state as
Both, the base flow ![]() $[\bar {u}_j(t), \ldots ]$ and the amplitudes
$[\bar {u}_j(t), \ldots ]$ and the amplitudes ![]() $[\skew 3\hat {u}_j(y, t), \ldots ]$ are
$[\skew 3\hat {u}_j(y, t), \ldots ]$ are ![]() $2{\rm \pi}$-periodic functions.
$2{\rm \pi}$-periodic functions. ![]() $k\in \mathbb {R}$ is the dimensionless perturbation wavenumber, and
$k\in \mathbb {R}$ is the dimensionless perturbation wavenumber, and ![]() $\sigma \in \mathbb {C}$ is the Floquet exponent. Note that the Floquet multiplier
$\sigma \in \mathbb {C}$ is the Floquet exponent. Note that the Floquet multiplier ![]() $\mu = \mathrm {e}^{2{\rm \pi} \sigma }$ is introduced such that
$\mu = \mathrm {e}^{2{\rm \pi} \sigma }$ is introduced such that ![]() $\mathrm {e}^{\sigma t} = \mu ^{t/(2{\rm \pi} )}$. Substitution of (2.19)–(2.22) into (2.7)–(2.12) yields
$\mathrm {e}^{\sigma t} = \mu ^{t/(2{\rm \pi} )}$. Substitution of (2.19)–(2.22) into (2.7)–(2.12) yields
subject to
 \begin{equation} \left. \begin{array}{ll@{}} y = H_2: & \skew3\hat{u}_2 = 0, \skew3\hat{v}_2 = 0,\\ y = h: & \skew3\hat{u}_j + \bar{u}_j'\skew3\hat{h} = 0, \skew3\hat{v}_1 = \skew3\hat{v}_2 = (\partial_t + \sigma) \skew3\hat{h},\\ y ={-}H_1: & \skew3\hat{u}_1 = 0, \skew3\hat{v}_1 = 0, \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{ll@{}} y = H_2: & \skew3\hat{u}_2 = 0, \skew3\hat{v}_2 = 0,\\ y = h: & \skew3\hat{u}_j + \bar{u}_j'\skew3\hat{h} = 0, \skew3\hat{v}_1 = \skew3\hat{v}_2 = (\partial_t + \sigma) \skew3\hat{h},\\ y ={-}H_1: & \skew3\hat{u}_1 = 0, \skew3\hat{v}_1 = 0, \end{array} \right\} \end{equation}
where ![]() $\mathcal {D}$ indicates partial
$\mathcal {D}$ indicates partial ![]() $y$ derivatives and
$y$ derivatives and ![]() $\mathcal {D}^n = \partial ^n/\partial y^n$. The kinematic boundary conditions at the perturbed interface in the normal direction,
$\mathcal {D}^n = \partial ^n/\partial y^n$. The kinematic boundary conditions at the perturbed interface in the normal direction, ![]() $u_j (x, y = h, t) = 0$, has been expanded in a Taylor series about its equilibrium value at
$u_j (x, y = h, t) = 0$, has been expanded in a Taylor series about its equilibrium value at ![]() $y = h$, i.e.
$y = h$, i.e.
where the primes indicate ![]() $y$ derivatives of the base flow, for example
$y$ derivatives of the base flow, for example ![]() $\bar {u}_j' = \partial \bar {u}_j/\partial y$. Leveraging the time-periodicity, the amplitude functions
$\bar {u}_j' = \partial \bar {u}_j/\partial y$. Leveraging the time-periodicity, the amplitude functions ![]() $[\skew 3\hat {u}_j(y,t), \ldots ]$ are expanded as Fourier series
$[\skew 3\hat {u}_j(y,t), \ldots ]$ are expanded as Fourier series ![]() $[\skew 3\hat {u}(y,t) = \sum _{n=-\infty }^{\infty } \skew 3\hat {u}_{j,n}(y) \mathrm {e}^{\mathrm {i} n t}, \ldots ]$,
$[\skew 3\hat {u}(y,t) = \sum _{n=-\infty }^{\infty } \skew 3\hat {u}_{j,n}(y) \mathrm {e}^{\mathrm {i} n t}, \ldots ]$, ![]() $n \in \mathbb {Z}$. Casting the base flow in the form
$n \in \mathbb {Z}$. Casting the base flow in the form ![]() $\bar {u}_j = \bar {u}_j^{\oplus }\mathrm {e}^{\mathrm {i} t} + \bar {u}_j^{\ominus }\mathrm {e}^{-\mathrm {i} t}$, yields the following set of coupled stability equations for
$\bar {u}_j = \bar {u}_j^{\oplus }\mathrm {e}^{\mathrm {i} t} + \bar {u}_j^{\ominus }\mathrm {e}^{-\mathrm {i} t}$, yields the following set of coupled stability equations for ![]() $n = -\infty, \ldots, 0 , \ldots,\infty$:
$n = -\infty, \ldots, 0 , \ldots,\infty$:
 $$\begin{gather}\left[ \sigma+\mathrm{i} n-{{Re}}^{{-}1}(\mathcal{D}^2-k^2) \right] \skew3\hat{u}_{j,n} + \bar{u}_j^{{\oplus}}\mathrm{i} k\skew3\hat{u}_{j,n-1} + \bar{u}_j^{{\ominus}}\mathrm{i} k\skew3\hat{u}_{j,n+1} \nonumber\\ +\, \bar{u}_j^{{\oplus}\prime} \skew3\hat{v}_{j,n-1} + \bar{u}_j^{{\ominus}\prime} \skew3\hat{v}_{j,n+1} + \mathrm{i} k\skew3\hat{p}_{j,n} = 0, \end{gather}$$
$$\begin{gather}\left[ \sigma+\mathrm{i} n-{{Re}}^{{-}1}(\mathcal{D}^2-k^2) \right] \skew3\hat{u}_{j,n} + \bar{u}_j^{{\oplus}}\mathrm{i} k\skew3\hat{u}_{j,n-1} + \bar{u}_j^{{\ominus}}\mathrm{i} k\skew3\hat{u}_{j,n+1} \nonumber\\ +\, \bar{u}_j^{{\oplus}\prime} \skew3\hat{v}_{j,n-1} + \bar{u}_j^{{\ominus}\prime} \skew3\hat{v}_{j,n+1} + \mathrm{i} k\skew3\hat{p}_{j,n} = 0, \end{gather}$$subject to
 \begin{equation} \left. \begin{array}{ll@{}} y = H_2: & \skew3\hat{u}_{2,n} = 0, \skew3\hat{v}_{2,n} = 0,\\ y = h: & \skew3\hat{u}_{j,n} + \bar{u}_j^{{\oplus}\prime} \skew3\hat{h}_{n-1} + \bar{u}_j^{{\ominus}\prime} \skew3\hat{h}_{n+1} = 0, \skew3\hat{v}_{1,n} = \skew3\hat{v}_{2,n} = (\sigma + \mathrm{i} n) \skew3\hat{h}_n,\\ y ={-}H_1: & \skew3\hat{u}_{1,n} = 0, \skew3\hat{v}_{1,n} = 0. \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{ll@{}} y = H_2: & \skew3\hat{u}_{2,n} = 0, \skew3\hat{v}_{2,n} = 0,\\ y = h: & \skew3\hat{u}_{j,n} + \bar{u}_j^{{\oplus}\prime} \skew3\hat{h}_{n-1} + \bar{u}_j^{{\ominus}\prime} \skew3\hat{h}_{n+1} = 0, \skew3\hat{v}_{1,n} = \skew3\hat{v}_{2,n} = (\sigma + \mathrm{i} n) \skew3\hat{h}_n,\\ y ={-}H_1: & \skew3\hat{u}_{1,n} = 0, \skew3\hat{v}_{1,n} = 0. \end{array} \right\} \end{equation}System (2.29)–(2.33) can be written in the form of a generalized eigenvalue problem
where the eigenvector ![]() $\boldsymbol {q} = [\ldots, \boldsymbol {q}_{-n}, \ldots, \boldsymbol {q}_{-1}, \boldsymbol {q}_0, \boldsymbol {q}_1, \ldots, \boldsymbol {q}_n, \ldots ]^\textrm {T}$ contains the Fourier modes
$\boldsymbol {q} = [\ldots, \boldsymbol {q}_{-n}, \ldots, \boldsymbol {q}_{-1}, \boldsymbol {q}_0, \boldsymbol {q}_1, \ldots, \boldsymbol {q}_n, \ldots ]^\textrm {T}$ contains the Fourier modes ![]() $\boldsymbol {q}_n = [\skew 3\hat {u}_{1,n}, \skew 3\hat {v}_{1,n}, \skew 3\hat {p}_{1,n}, \skew 3\hat {u}_{2,n}, \skew 3\hat {v}_{2,n}, \skew 3\hat {p}_{2,n}, \skew 3\hat {h}_n]^\textrm {T}$ that in turn contain all perturbation quantities.
$\boldsymbol {q}_n = [\skew 3\hat {u}_{1,n}, \skew 3\hat {v}_{1,n}, \skew 3\hat {p}_{1,n}, \skew 3\hat {u}_{2,n}, \skew 3\hat {v}_{2,n}, \skew 3\hat {p}_{2,n}, \skew 3\hat {h}_n]^\textrm {T}$ that in turn contain all perturbation quantities.
The eigenvalues ![]() $\sigma$ or, equivalently, the corresponding Floquet multipliers
$\sigma$ or, equivalently, the corresponding Floquet multipliers ![]() $\mu = \mathrm {e}^{2{\rm \pi} \sigma }$, determine the linear stability of the two-layer system. When, for a certain combination of governing parameters
$\mu = \mathrm {e}^{2{\rm \pi} \sigma }$, determine the linear stability of the two-layer system. When, for a certain combination of governing parameters ![]() $(\mathcal {K}, { {Re}}, H_1, H_2)$ and for a certain wavenumber
$(\mathcal {K}, { {Re}}, H_1, H_2)$ and for a certain wavenumber ![]() $k$, all
$k$, all ![]() $|\mu | < 1$, the system is linearly stable to all perturbations of wavelength
$|\mu | < 1$, the system is linearly stable to all perturbations of wavelength ![]() $2{\rm \pi} /k$. In the present work, we are concerned with obtaining the conditions for marginal stability, i.e. the values of
$2{\rm \pi} /k$. In the present work, we are concerned with obtaining the conditions for marginal stability, i.e. the values of ![]() $(\mathcal {K}, { {Re}}, H_1, H_2)$ and
$(\mathcal {K}, { {Re}}, H_1, H_2)$ and ![]() $k$ for which a single value of
$k$ for which a single value of ![]() $\mu$ crosses the unit circle
$\mu$ crosses the unit circle ![]() $|\mu | = 1$.
$|\mu | = 1$.
3. Numerical method
The system of stability equations (2.29)–(2.33) is solved numerically using a finite number ![]() $N$ of Fourier modes. A Chebyshev collocation method is used for the spatial discretization in the wall-normal (
$N$ of Fourier modes. A Chebyshev collocation method is used for the spatial discretization in the wall-normal (![]() $y$) direction, employing a number
$y$) direction, employing a number ![]() $M_1$ of collocation points in layer 1, and
$M_1$ of collocation points in layer 1, and ![]() $M_2$ points in layer 2. Since the
$M_2$ points in layer 2. Since the ![]() $n$th Fourier mode is only coupled with modes
$n$th Fourier mode is only coupled with modes ![]() $n-1$ and
$n-1$ and ![]() $n+1$, the general structure of the discretized eigenvalue problem is block-tridiagonal,
$n+1$, the general structure of the discretized eigenvalue problem is block-tridiagonal,
 \begin{align} &\begin{bmatrix} & & & & & & & & & \\ & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{L}}_{n-1}^{n-2} & \boldsymbol{\mathsf{L}}_{n-1}^{n-1} & \boldsymbol{\mathsf{L}}_{n-1}^{n} & \boldsymbol{0} & \cdots & & \\ & & & & & & & \\ & & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{L}}_{n}^{n-1} & \boldsymbol{\mathsf{L}}_{n}^{n} & \boldsymbol{\mathsf{L}}_{n}^{n+1} & \boldsymbol{0} & \cdots & \\ & & & & & & & \\ & & & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{L}}_{n+1}^{n} & \boldsymbol{\mathsf{L}}_{n+1}^{n+1} & \boldsymbol{\mathsf{L}}_{n+1}^{n+2} & \boldsymbol{0} & \cdots\\ & & & & & & & \end{bmatrix} \begin{bmatrix} \vdots \\ \boldsymbol{q}_{n-1} \\ \boldsymbol{q}_n \\ \boldsymbol{q}_{n+1} \\ \vdots \end{bmatrix}\nonumber\\ &\qquad = \sigma \begin{bmatrix} & & & & & & \\ & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{B}}_{n-1}^{n-1} & \boldsymbol{0} & \cdots & & \\ & & & & & \\ & & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{B}}_{n}^{n} & \boldsymbol{0} & \cdots & \\ & & & & & \\ & & & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{B}}_{n+1}^{n+1} & \boldsymbol{0} & \cdots\\ & & & & & & & \end{bmatrix} \begin{bmatrix} \vdots \\ \boldsymbol{q}_{n-1} \\ \boldsymbol{q}_n \\ \boldsymbol{q}_{n+1} \\ \vdots \end{bmatrix}, \end{align}
\begin{align} &\begin{bmatrix} & & & & & & & & & \\ & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{L}}_{n-1}^{n-2} & \boldsymbol{\mathsf{L}}_{n-1}^{n-1} & \boldsymbol{\mathsf{L}}_{n-1}^{n} & \boldsymbol{0} & \cdots & & \\ & & & & & & & \\ & & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{L}}_{n}^{n-1} & \boldsymbol{\mathsf{L}}_{n}^{n} & \boldsymbol{\mathsf{L}}_{n}^{n+1} & \boldsymbol{0} & \cdots & \\ & & & & & & & \\ & & & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{L}}_{n+1}^{n} & \boldsymbol{\mathsf{L}}_{n+1}^{n+1} & \boldsymbol{\mathsf{L}}_{n+1}^{n+2} & \boldsymbol{0} & \cdots\\ & & & & & & & \end{bmatrix} \begin{bmatrix} \vdots \\ \boldsymbol{q}_{n-1} \\ \boldsymbol{q}_n \\ \boldsymbol{q}_{n+1} \\ \vdots \end{bmatrix}\nonumber\\ &\qquad = \sigma \begin{bmatrix} & & & & & & \\ & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{B}}_{n-1}^{n-1} & \boldsymbol{0} & \cdots & & \\ & & & & & \\ & & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{B}}_{n}^{n} & \boldsymbol{0} & \cdots & \\ & & & & & \\ & & & \cdots & \boldsymbol{0} & \boldsymbol{\mathsf{B}}_{n+1}^{n+1} & \boldsymbol{0} & \cdots\\ & & & & & & & \end{bmatrix} \begin{bmatrix} \vdots \\ \boldsymbol{q}_{n-1} \\ \boldsymbol{q}_n \\ \boldsymbol{q}_{n+1} \\ \vdots \end{bmatrix}, \end{align}
where each set of square submatrices ![]() $\boldsymbol{\mathsf{L}}_{n}^{n\pm 1}$ and
$\boldsymbol{\mathsf{L}}_{n}^{n\pm 1}$ and ![]() $\boldsymbol{\mathsf{B}}_{n}^{n\pm 1}$, of size
$\boldsymbol{\mathsf{B}}_{n}^{n\pm 1}$, of size ![]() $3(M_1+M_2)+1$, contains the discretized stability equations (2.29)–(2.33). Their rows are arranged such that the first
$3(M_1+M_2)+1$, contains the discretized stability equations (2.29)–(2.33). Their rows are arranged such that the first ![]() $3M_1$ rows encode the continuity and momentum equations (2.29)–(2.31) for the fluid in layer 1, the next
$3M_1$ rows encode the continuity and momentum equations (2.29)–(2.31) for the fluid in layer 1, the next ![]() $3M_2$ rows encode the corresponding equations for the fluid in layer 2, and the last row contains the fluid–solid interaction equation (2.32). The boundary conditions (2.33) are implemented by replacing the corresponding rows in
$3M_2$ rows encode the corresponding equations for the fluid in layer 2, and the last row contains the fluid–solid interaction equation (2.32). The boundary conditions (2.33) are implemented by replacing the corresponding rows in ![]() $\boldsymbol{\mathsf{L}}_{n}^{n\pm 1}$ and
$\boldsymbol{\mathsf{L}}_{n}^{n\pm 1}$ and ![]() $\boldsymbol{\mathsf{B}}_{n}^{n\pm 1}$.
$\boldsymbol{\mathsf{B}}_{n}^{n\pm 1}$.
The numerical implementation was performed in MATLAB. The number of Fourier modes ![]() $N$ and the number of discretization points
$N$ and the number of discretization points ![]() $M_1$,
$M_1$, ![]() $M_2$ was increased until numerical convergence was obtained (a varying number of points was needed for varying layer depths
$M_2$ was increased until numerical convergence was obtained (a varying number of points was needed for varying layer depths ![]() $H_1$ and
$H_1$ and ![]() $H_2$ and varying Reynolds numbers
$H_2$ and varying Reynolds numbers ![]() ${ {Re}}$). For all cases,
${ {Re}}$). For all cases, ![]() $N=10$ Fourier modes was found to be sufficient, whereas
$N=10$ Fourier modes was found to be sufficient, whereas ![]() $M_1$ and
$M_1$ and ![]() $M_2$ ranged from 48 to 128.
$M_2$ ranged from 48 to 128.
4. Results
4.1. Floquet eigenvalues and eigenmode analysis
The numerical solution of the eigenvalue problem that determines the linear Floquet stability of the two-layer configuration for a particular combination of canal widths ![]() $H_1$ and
$H_1$ and ![]() $H_2$, stiffness
$H_2$, stiffness ![]() $\mathcal {K}$, Reynolds number
$\mathcal {K}$, Reynolds number ![]() ${ {Re}}$ and perturbation wavenumber
${ {Re}}$ and perturbation wavenumber ![]() $k$, yields a spectrum of eigenvalues
$k$, yields a spectrum of eigenvalues ![]() $\sigma$, or, correspondingly, a spectrum of Floquet multipliers
$\sigma$, or, correspondingly, a spectrum of Floquet multipliers ![]() $\mu = \mathrm {e}^{2{\rm \pi} \sigma }$. The insets of figure 4 show such spectra for
$\mu = \mathrm {e}^{2{\rm \pi} \sigma }$. The insets of figure 4 show such spectra for ![]() $\mathcal {K} = 1$,
$\mathcal {K} = 1$, ![]() $H_1 = H_2 = \infty$,
$H_1 = H_2 = \infty$, ![]() ${ {Re}} = 25.9$ and three values of the wavenumber
${ {Re}} = 25.9$ and three values of the wavenumber ![]() $k = (0.8, 1.5, 2.2)$. Whereas for the smallest and largest wavenumbers the most unstable mode has a non-zero imaginary part (left-hand and right-hand inset), there is a band of intermediate wavenumbers for which the most unstable mode is purely real (middle inset), corresponding to perturbations of the flow field that oscillate synchronous with the base flow. It is this branch of Floquet modes that gets most amplified when the Reynolds number increases (compare in figure 4 the curve
$k = (0.8, 1.5, 2.2)$. Whereas for the smallest and largest wavenumbers the most unstable mode has a non-zero imaginary part (left-hand and right-hand inset), there is a band of intermediate wavenumbers for which the most unstable mode is purely real (middle inset), corresponding to perturbations of the flow field that oscillate synchronous with the base flow. It is this branch of Floquet modes that gets most amplified when the Reynolds number increases (compare in figure 4 the curve ![]() $\mu (k)$ for
$\mu (k)$ for ![]() ${ {Re}} = 20$ with that for
${ {Re}} = 20$ with that for ![]() ${ {Re}} = 25.9$), crossing the unit circle
${ {Re}} = 25.9$), crossing the unit circle ![]() $|\mu | = 1$ for
$|\mu | = 1$ for ![]() $k = 1.5$ and
$k = 1.5$ and ![]() ${ {Re}} = 25.9$. A curve of marginal stability can be traced in the
${ {Re}} = 25.9$. A curve of marginal stability can be traced in the ![]() $({ {Re}}-k)$ plane by obtaining, for each value of
$({ {Re}}-k)$ plane by obtaining, for each value of ![]() $k$, the value of
$k$, the value of ![]() ${ {Re}}$ for which the most unstable mode has
${ {Re}}$ for which the most unstable mode has ![]() $|\mu | = 1$ (figure 5). We can then define a critical Reynolds number,
$|\mu | = 1$ (figure 5). We can then define a critical Reynolds number, ![]() ${ {Re}}_{cr}$, indicated in figure 5 with a dot, as the minimum
${ {Re}}_{cr}$, indicated in figure 5 with a dot, as the minimum ![]() ${ {Re}}$-value of the marginal curve. Note that the value
${ {Re}}$-value of the marginal curve. Note that the value ![]() ${ {Re}}_{cr} = 25.9$ of figure 5 corresponds of course to the critical condition shown in figure 4. The condition
${ {Re}}_{cr} = 25.9$ of figure 5 corresponds of course to the critical condition shown in figure 4. The condition ![]() $({ {Re}} = 25.9, \mathcal {K} = 1, H_1 = \infty, H_2 = \infty )$ thus lies on the marginal surface delimiting the linearly stable and unstable regimes in the parameter space spanned by
$({ {Re}} = 25.9, \mathcal {K} = 1, H_1 = \infty, H_2 = \infty )$ thus lies on the marginal surface delimiting the linearly stable and unstable regimes in the parameter space spanned by ![]() ${ {Re}}, \mathcal {K}, H_1 \ \textrm {and}\ H_2$. In § 4.2 different slices in this space are explored to see the individual influence of the different physical parameters on the stability of the system.
${ {Re}}, \mathcal {K}, H_1 \ \textrm {and}\ H_2$. In § 4.2 different slices in this space are explored to see the individual influence of the different physical parameters on the stability of the system.

Figure 4. Floquet growth rate ![]() $|\mu |$ as a function of the perturbation wavenumber
$|\mu |$ as a function of the perturbation wavenumber ![]() $k$, for two values of the Reynolds number,
$k$, for two values of the Reynolds number, ![]() ${ {Re}} = 20$ and
${ {Re}} = 20$ and ![]() ${ {Re}} = 25.9$, and
${ {Re}} = 25.9$, and ![]() $\mathcal {K} = 1$,
$\mathcal {K} = 1$, ![]() $H_1 = H_2 \rightarrow \infty$. Insets show the spectra of Floquet multipliers
$H_1 = H_2 \rightarrow \infty$. Insets show the spectra of Floquet multipliers ![]() $\mu$ for three different wavenumbers. The critical conditions correspond to
$\mu$ for three different wavenumbers. The critical conditions correspond to ![]() ${ {Re}} = 25.9$ and
${ {Re}} = 25.9$ and ![]() $k = 1.5$.
$k = 1.5$.

Figure 5. The curve of marginal stability corresponding to ![]() $|\mu | = 1$ in the
$|\mu | = 1$ in the ![]() $({ {Re}}, k)$ plane, for
$({ {Re}}, k)$ plane, for ![]() $\mathcal {K} = 1$ and
$\mathcal {K} = 1$ and ![]() $H_2 = H_1 = \infty$. The critical Reynolds number
$H_2 = H_1 = \infty$. The critical Reynolds number ![]() ${ {Re}}_{cr}$, indicated with a dot, is defined as the minimum
${ {Re}}_{cr}$, indicated with a dot, is defined as the minimum ![]() ${ {Re}}$ value of the marginal curve. Note that the value
${ {Re}}$ value of the marginal curve. Note that the value ![]() ${ {Re}}_{cr} = 25.9$ corresponds to the critical condition shown in figure 4.
${ {Re}}_{cr} = 25.9$ corresponds to the critical condition shown in figure 4.
Figure 6 shows the time evolution of the perturbation eigenvector (figure 6a), together with that of the total, perturbed, flow (figure 6b), computed as the superposition of the perturbation eigenvector and the base flow, ![]() $(\bar {u}_{1,2}, \bar {v}_{1,2}) + 0.1 (\skew 3\hat {u}_{1,2}, \skew 3\hat {v}_{1,2}) \mathrm {e}^{\mathrm {i} k x} \mathrm {e}^{\sigma t}$, over the course of one oscillation cycle (with dimensionless period
$(\bar {u}_{1,2}, \bar {v}_{1,2}) + 0.1 (\skew 3\hat {u}_{1,2}, \skew 3\hat {v}_{1,2}) \mathrm {e}^{\mathrm {i} k x} \mathrm {e}^{\sigma t}$, over the course of one oscillation cycle (with dimensionless period ![]() $T = 2{\rm \pi}$), for the marginally unstable case
$T = 2{\rm \pi}$), for the marginally unstable case ![]() $k = 1.52$,
$k = 1.52$, ![]() ${ {Re}} = 26$,
${ {Re}} = 26$, ![]() $K = 1$,
$K = 1$, ![]() $H_1 = 3$,
$H_1 = 3$, ![]() $H_2 = 4$. Note that the perturbation eigenvector is normalized such that
$H_2 = 4$. Note that the perturbation eigenvector is normalized such that ![]() $[\int _{-H_1}^{H_2} (\skew 3\hat {u}^{\dagger} \skew 3\hat {u} + \skew 3\hat {v}^{\dagger} \skew 3\hat {v}) \,\mathrm {d} y]^{1/2} = 1$, where here
$[\int _{-H_1}^{H_2} (\skew 3\hat {u}^{\dagger} \skew 3\hat {u} + \skew 3\hat {v}^{\dagger} \skew 3\hat {v}) \,\mathrm {d} y]^{1/2} = 1$, where here ![]() ${\dagger}$ indicates the complex conjugate. Vectors indicate the direction of the flow and colour represents the magnitude of the velocity perturbation in figure 6(a), and of its superposition with the base flow in figure 6(b). The perturbation corrugates the separating wall in a time-periodic fashion, with an associated spatially periodic perturbed flow field that decays in the transverse direction
${\dagger}$ indicates the complex conjugate. Vectors indicate the direction of the flow and colour represents the magnitude of the velocity perturbation in figure 6(a), and of its superposition with the base flow in figure 6(b). The perturbation corrugates the separating wall in a time-periodic fashion, with an associated spatially periodic perturbed flow field that decays in the transverse direction ![]() $y$ towards the upper and lower bounding walls. The spatial wavelength is dictated by the wavenumber
$y$ towards the upper and lower bounding walls. The spatial wavelength is dictated by the wavenumber ![]() $k$ as
$k$ as ![]() $2{\rm \pi} /k = 4.1$, being
$2{\rm \pi} /k = 4.1$, being ![]() $k=1.52$ in this case.
$k=1.52$ in this case.

Figure 6. Time evolution of (a) the perturbation eigenvector alone and (b) the total, perturbed, flow, computed as the superposition of the perturbation eigenvector and the base flow, ![]() $(\bar {u}_{1,2}, \bar {v}_{1,2}) + 0.1 (\skew 3\hat {u}_{1,2}, \skew 3\hat {v}_{1,2}) \mathrm {e}^{\mathrm {i} k x} \mathrm {e}^{\sigma t}$, over the course of one oscillation cycle (with dimensionless period
$(\bar {u}_{1,2}, \bar {v}_{1,2}) + 0.1 (\skew 3\hat {u}_{1,2}, \skew 3\hat {v}_{1,2}) \mathrm {e}^{\mathrm {i} k x} \mathrm {e}^{\sigma t}$, over the course of one oscillation cycle (with dimensionless period ![]() $T = 2{\rm \pi}$), for the marginally unstable case
$T = 2{\rm \pi}$), for the marginally unstable case ![]() ${k = 1.52}$,
${k = 1.52}$, ![]() ${ {Re}} = 26$,
${ {Re}} = 26$, ![]() $K = 1$,
$K = 1$, ![]() $H_1 = 3$,
$H_1 = 3$, ![]() $H_2 = 4$.
$H_2 = 4$.
4.2. Influence of the canal widths  $H_1$,
$H_1$,  $H_2$ and the wall stiffness
$H_2$ and the wall stiffness  $\mathcal {K}$ on the onset of instability
$\mathcal {K}$ on the onset of instability
A parametric analysis has been carried out to study the influence of the widths ![]() $H_1$ and
$H_1$ and ![]() $H_2$ of the two fluid layers and the wall stiffness
$H_2$ of the two fluid layers and the wall stiffness ![]() $\mathcal {K}$ on the linear Floquet stability of the system. Curves of marginal stability in the
$\mathcal {K}$ on the linear Floquet stability of the system. Curves of marginal stability in the ![]() $({ {Re}}, k)$ plane for different values of
$({ {Re}}, k)$ plane for different values of ![]() $H_1$ are given for two illustrative cases:
$H_1$ are given for two illustrative cases: ![]() $H_2 \rightarrow \infty$,
$H_2 \rightarrow \infty$, ![]() $\mathcal {K} = 1$ (figure 7a); and
$\mathcal {K} = 1$ (figure 7a); and ![]() $H_2 = 1$,
$H_2 = 1$, ![]() $\mathcal {K} = 1$ (figure 7b). Reducing the canal width has a stabilizing effect, increasing the Reynolds number associated with the onset of instability over the entire range of wavenumbers studied here. The most unstable wavenumber, corresponding to the critical Reynolds numbers indicated by the dots in figure 7, is not influenced appreciably by the canal widths, remaining close to
$\mathcal {K} = 1$ (figure 7b). Reducing the canal width has a stabilizing effect, increasing the Reynolds number associated with the onset of instability over the entire range of wavenumbers studied here. The most unstable wavenumber, corresponding to the critical Reynolds numbers indicated by the dots in figure 7, is not influenced appreciably by the canal widths, remaining close to ![]() $k = 1.5$ for the value
$k = 1.5$ for the value ![]() $\mathcal {K} = 1$ studied in figure 7, although a slight decrease of the most unstable wavenumber can be inferred in figure 7(b) as
$\mathcal {K} = 1$ studied in figure 7, although a slight decrease of the most unstable wavenumber can be inferred in figure 7(b) as ![]() $H_1$ increases for
$H_1$ increases for ![]() $H_2=1$.
$H_2=1$.

Figure 7. Curves of marginal stability in the ![]() $({ {Re}}, k)$ plane, for various values of
$({ {Re}}, k)$ plane, for various values of ![]() $H_1$ for the cases
$H_1$ for the cases ![]() $({H_2 = \infty}, {\mathcal {K} = 1})$ (a) and
$({H_2 = \infty}, {\mathcal {K} = 1})$ (a) and ![]() $(H_2 = 1, \mathcal {K} = 1)$ (b). Solid dots indicate the critical Reynolds number
$(H_2 = 1, \mathcal {K} = 1)$ (b). Solid dots indicate the critical Reynolds number ![]() ${ {Re}}_{cr}$ as the minimum
${ {Re}}_{cr}$ as the minimum ![]() ${ {Re}}$-value of each marginal curve.
${ {Re}}$-value of each marginal curve.
Figure 8 slices the parameter space ![]() $({ {Re}}, H_1, H_2, \mathcal {K})$ by showing how the critical Reynolds number varies with
$({ {Re}}, H_1, H_2, \mathcal {K})$ by showing how the critical Reynolds number varies with ![]() $H_1$, for various values of
$H_1$, for various values of ![]() $H_2$, and for four values of
$H_2$, and for four values of ![]() $\mathcal {K}$, corresponding to figure 8(a–d). The stabilizing influence of decreasing the canal widths
$\mathcal {K}$, corresponding to figure 8(a–d). The stabilizing influence of decreasing the canal widths ![]() $H_1$ and
$H_1$ and ![]() $H_2$ becomes more pronounced the thinner the canals become. This is indicated both by the slope of the marginal curves near
$H_2$ becomes more pronounced the thinner the canals become. This is indicated both by the slope of the marginal curves near ![]() $H_1 = 1$ and by the distance between the different marginal curves for different
$H_1 = 1$ and by the distance between the different marginal curves for different ![]() $H_2$. At this point, it is worth pointing out that, because of the symmetry of the configuration,
$H_2$. At this point, it is worth pointing out that, because of the symmetry of the configuration, ![]() $H_1$ and
$H_1$ and ![]() $H_2$ are completely interchangeable in the analysis. The stabilizing effect of confinement originates from the imposed attenuation of the velocity perturbations at the lateral walls (boundary condition (2.33)). When unconfined (
$H_2$ are completely interchangeable in the analysis. The stabilizing effect of confinement originates from the imposed attenuation of the velocity perturbations at the lateral walls (boundary condition (2.33)). When unconfined (![]() $H_1 \rightarrow \infty$ and/or
$H_1 \rightarrow \infty$ and/or ![]() $H_2 \rightarrow \infty$), the eigenfunction decays exponentially in the transverse direction over a distance that scales with the perturbation wavelength
$H_2 \rightarrow \infty$), the eigenfunction decays exponentially in the transverse direction over a distance that scales with the perturbation wavelength ![]() $2{\rm \pi} /k$ (stemming from the
$2{\rm \pi} /k$ (stemming from the ![]() $\mathcal {D}^2 - k^2$ operator in the stability equations (2.30)–(2.31)). This is illustrated in figure 9, which shows the velocity perturbation
$\mathcal {D}^2 - k^2$ operator in the stability equations (2.30)–(2.31)). This is illustrated in figure 9, which shows the velocity perturbation ![]() $\hat {u}_2(y, t)$ at eight instants of time over the course of one cycle for two critical cases, one case with a large wavenumber (
$\hat {u}_2(y, t)$ at eight instants of time over the course of one cycle for two critical cases, one case with a large wavenumber (![]() $k = 1.94$,
$k = 1.94$, ![]() $\mathcal {K} = 0.5$,
$\mathcal {K} = 0.5$, ![]() ${ {Re}} = 30.1$, figure 9a), and another one with a small wavenumber (
${ {Re}} = 30.1$, figure 9a), and another one with a small wavenumber (![]() $k = 0.76$,
$k = 0.76$, ![]() $\mathcal {K} = 2.7$,
$\mathcal {K} = 2.7$, ![]() ${ {Re}} = 21.31$, figure 9b). As commented previously, when changing
${ {Re}} = 21.31$, figure 9b). As commented previously, when changing ![]() $H_1$ or
$H_1$ or ![]() $H_2$, the most unstable wavenumber, corresponding to
$H_2$, the most unstable wavenumber, corresponding to ![]() ${ {Re}}_{cr}$, hardly changes. Therefore, for smaller wavenumbers (larger wavelengths), the transverse extent of the eigenfunctions being larger leads to the effect that decreasing
${ {Re}}_{cr}$, hardly changes. Therefore, for smaller wavenumbers (larger wavelengths), the transverse extent of the eigenfunctions being larger leads to the effect that decreasing ![]() $H_1$ and/or
$H_1$ and/or ![]() $H_2$ on the critical Reynolds number is noticed earlier (larger
$H_2$ on the critical Reynolds number is noticed earlier (larger ![]() $H_1$ or
$H_1$ or ![]() $H_2$). On the contrary, for larger wavenumbers (smaller wavelengths), the eigenfunctions extend over a smaller distance, and the confinement is noticed later (smaller
$H_2$). On the contrary, for larger wavenumbers (smaller wavelengths), the eigenfunctions extend over a smaller distance, and the confinement is noticed later (smaller ![]() $H_1$ or
$H_1$ or ![]() $H_2$). This also explains why the influence of
$H_2$). This also explains why the influence of ![]() $H_1$ and
$H_1$ and ![]() $H_2$ occurs at different rates for the four panels of figure 8. Each panel corresponds to a different value of
$H_2$ occurs at different rates for the four panels of figure 8. Each panel corresponds to a different value of ![]() $\mathcal {K}$ and has a different associated wavenumber
$\mathcal {K}$ and has a different associated wavenumber ![]() $k$.
$k$.

Figure 8. Variation of the critical Reynolds number ![]() ${ {Re}}_{cr}$ with
${ {Re}}_{cr}$ with ![]() $H_1$, for different values of
$H_1$, for different values of ![]() $H_2$, and four values of
$H_2$, and four values of ![]() $\mathcal {K}$: (a)
$\mathcal {K}$: (a) ![]() $\mathcal {K}=0.5$; (b)
$\mathcal {K}=0.5$; (b) ![]() $\mathcal {K}=1$; (c)
$\mathcal {K}=1$; (c) ![]() $\mathcal {K}=2$; and (d)
$\mathcal {K}=2$; and (d) ![]() $\mathcal {K}=2.7$. Note that the wavenumber is approximately
$\mathcal {K}=2.7$. Note that the wavenumber is approximately ![]() $k \simeq 1.94$ for all cases in (a);
$k \simeq 1.94$ for all cases in (a); ![]() $k \simeq 1.5$ for all cases in (b);
$k \simeq 1.5$ for all cases in (b); ![]() $k \simeq 0.98$ for all cases in (c); and
$k \simeq 0.98$ for all cases in (c); and ![]() $k \simeq 0.76$ for all cases in (d).
$k \simeq 0.76$ for all cases in (d).

Figure 9. Velocity perturbation ![]() $\hat {u}_2(y, t)$ for two marginally stable cases for
$\hat {u}_2(y, t)$ for two marginally stable cases for ![]() $H_1\rightarrow \infty$ and
$H_1\rightarrow \infty$ and ![]() $H_2 \rightarrow \infty$:(a)
$H_2 \rightarrow \infty$:(a) ![]() $k = 1.94$,
$k = 1.94$, ![]() $\mathcal {K} = 0.5$ and
$\mathcal {K} = 0.5$ and ![]() ${ {Re}} = 30.1$; and (b)
${ {Re}} = 30.1$; and (b) ![]() $k = 0.76$,
$k = 0.76$, ![]() $\mathcal {K} = 2.7$ and
$\mathcal {K} = 2.7$ and ![]() ${ {Re}} = 21.31$. The longer the wavelength
${ {Re}} = 21.31$. The longer the wavelength ![]() $2{\rm \pi} /k$, the slower the transverse decay of the perturbations.
$2{\rm \pi} /k$, the slower the transverse decay of the perturbations.
The occurrence of the instability and its associated wavenumber strongly depends on the value of the dimensionless stiffness ![]() $\mathcal {K}$. Figure 10 shows, in blue, how the most unstable wavenumber
$\mathcal {K}$. Figure 10 shows, in blue, how the most unstable wavenumber ![]() $k_{uns}$ decreases with increasing stiffness
$k_{uns}$ decreases with increasing stiffness ![]() $\mathcal {K}$ for symmetric channel configurations (
$\mathcal {K}$ for symmetric channel configurations (![]() $H_1 = H_2$). Note that, in agreement with the results presented before, in the range
$H_1 = H_2$). Note that, in agreement with the results presented before, in the range ![]() $1 \leq H_1=H_2 < \infty$ studied here,
$1 \leq H_1=H_2 < \infty$ studied here, ![]() $k_{uns}(\mathcal {K})$ is essentially independent of
$k_{uns}(\mathcal {K})$ is essentially independent of ![]() $H_1$ and
$H_1$ and ![]() $H_2$, and can therefore be presented in figure 10 as a single curve. The family of green curves in this figure represents the dependence of the critical Reynolds number,
$H_2$, and can therefore be presented in figure 10 as a single curve. The family of green curves in this figure represents the dependence of the critical Reynolds number, ![]() ${ {Re}}_{cr}$, with
${ {Re}}_{cr}$, with ![]() $\mathcal {K}$. Except for the case
$\mathcal {K}$. Except for the case ![]() $H_1 = H_2 = 1$, there exist a value of
$H_1 = H_2 = 1$, there exist a value of ![]() $\mathcal {K}$ for which the
$\mathcal {K}$ for which the ![]() ${ {Re}}_{cr}$ is minimum. This minimum depends on the channel configuration, with the unbounded case being the most unstable, in the sense of exhibiting the lowest value of
${ {Re}}_{cr}$ is minimum. This minimum depends on the channel configuration, with the unbounded case being the most unstable, in the sense of exhibiting the lowest value of ![]() ${ {Re}}_{cr}$ (
${ {Re}}_{cr}$ (![]() $\mathcal {K} \simeq 3$). The dimensionless wall stiffness
$\mathcal {K} \simeq 3$). The dimensionless wall stiffness ![]() $\mathcal {K}$ can be interpreted as the inverse of the square root of a reduced velocity, i.e.
$\mathcal {K}$ can be interpreted as the inverse of the square root of a reduced velocity, i.e. ![]() $\sqrt {1/\mathcal {K}} = \sqrt {\rho l^{\ast }/{\mathcal {K}^\ast }} / ({\omega ^\ast }^{-1})$, which is the ratio of the characteristic time associated with the spring-backed wall moving the adjacent fluid layer in the transverse direction, and the longitudinal oscillation time of the basic fluid motion. Therefore, optimal fluid–structure interaction can be expected for order-unity values of
$\sqrt {1/\mathcal {K}} = \sqrt {\rho l^{\ast }/{\mathcal {K}^\ast }} / ({\omega ^\ast }^{-1})$, which is the ratio of the characteristic time associated with the spring-backed wall moving the adjacent fluid layer in the transverse direction, and the longitudinal oscillation time of the basic fluid motion. Therefore, optimal fluid–structure interaction can be expected for order-unity values of ![]() $\mathcal {K}$, in agreement with the non-monotonic behaviour of the marginal stability curves of figure 10.
$\mathcal {K}$, in agreement with the non-monotonic behaviour of the marginal stability curves of figure 10.

Figure 10. Critical Reynolds number ![]() ${ {Re}}_{cr}$ and corresponding wavenumber
${ {Re}}_{cr}$ and corresponding wavenumber ![]() $k_{uns}$ as a function of the wall stiffness
$k_{uns}$ as a function of the wall stiffness ![]() $\mathcal {K}$ in symmetric channel configurations with
$\mathcal {K}$ in symmetric channel configurations with ![]() $H_1 = H_2= 1, 1.25, 1.5, 2, 3, 4, \infty$.
$H_1 = H_2= 1, 1.25, 1.5, 2, 3, 4, \infty$.
In the limit of vanishing wall flexibility, i.e. when the spring stiffness ![]() $\mathcal {K}\to \infty$, the problem configuration reduces to that of oscillatory flow in a channel with rigid walls, which, for
$\mathcal {K}\to \infty$, the problem configuration reduces to that of oscillatory flow in a channel with rigid walls, which, for ![]() $H_1, H_2 \to \infty$ further reduces to the oscillatory Stokes-layer flow over a rigid wall. The linear stability of the Stokes layer was first studied by Hall (Reference Hall1978), and revisited by Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002), who determined that the onset of instability occurs when the Reynolds number, based on the shear-layer thickness
$H_1, H_2 \to \infty$ further reduces to the oscillatory Stokes-layer flow over a rigid wall. The linear stability of the Stokes layer was first studied by Hall (Reference Hall1978), and revisited by Blennerhassett & Bassom (Reference Blennerhassett and Bassom2002), who determined that the onset of instability occurs when the Reynolds number, based on the shear-layer thickness ![]() $\sqrt {2\nu /{\omega ^\ast }}$,
$\sqrt {2\nu /{\omega ^\ast }}$, ![]() ${ {Re}}_{BB} = {U^\ast } \sqrt {2\nu /{\omega ^\ast }}/(2\nu ) = 708$, for perturbations of wavelength
${ {Re}}_{BB} = {U^\ast } \sqrt {2\nu /{\omega ^\ast }}/(2\nu ) = 708$, for perturbations of wavelength ![]() $\lambda _{BB} = \lambda ^\ast / \sqrt {2\nu /{\omega ^\ast }} = 2{\rm \pi} /0.38$. In terms of the scales employed in the present analysis, this means a Reynolds number
$\lambda _{BB} = \lambda ^\ast / \sqrt {2\nu /{\omega ^\ast }} = 2{\rm \pi} /0.38$. In terms of the scales employed in the present analysis, this means a Reynolds number ![]() ${ {Re}} = 2 { {Re}}_{BB}^2 \simeq 10^6$ and a wavelength
${ {Re}} = 2 { {Re}}_{BB}^2 \simeq 10^6$ and a wavelength ![]() $\lambda = \lambda ^\ast /l^\ast = \lambda _{BB}/{ {Re}}_{BB} \simeq 2{\rm \pi} /270$. Thus, the conditions for which the wall deformation is optimally coupled to the oscillatory fluid motion, found here for
$\lambda = \lambda ^\ast /l^\ast = \lambda _{BB}/{ {Re}}_{BB} \simeq 2{\rm \pi} /270$. Thus, the conditions for which the wall deformation is optimally coupled to the oscillatory fluid motion, found here for ![]() $\mathcal {K}$ of order unity and
$\mathcal {K}$ of order unity and ![]() ${ {Re}} \sim 20-30$ lie very far away from the critical conditions for the onset instability in the Stokes layer near a rigid wall. Capturing the transition from the present problem to its rigid counterpart requires a different treatment, using the shear-layer thickness instead of the stroke length as characteristic length scale, and lies out of the scope of the present work.
${ {Re}} \sim 20-30$ lie very far away from the critical conditions for the onset instability in the Stokes layer near a rigid wall. Capturing the transition from the present problem to its rigid counterpart requires a different treatment, using the shear-layer thickness instead of the stroke length as characteristic length scale, and lies out of the scope of the present work.
4.3. Influence of additional damping
As detailed and discussed in § 2.1, the choice of the particular fluid–structure interaction model considered here, i.e. the massless undamped spring-backed plate, is motivated by the cerebrospinal fluid flow on both sides of the spinal cord in subjects with syringomyelia, the springs mimicking microanatomical features that keep the spinal cord in place within the spinal canal. Now, we briefly explore the effect of including a damping term in (2.10),
where ![]() $\unicode{x1D4B9}$
$\unicode{x1D4B9}$ ![]() $= d^\ast {\omega ^\ast }/{\varPi _\ell ^\ast }$. This term is related with the amount of energy irreversibly removed from the wall. In the particular problem under consideration here, the order of the damping coefficient is estimated to be around
$= d^\ast {\omega ^\ast }/{\varPi _\ell ^\ast }$. This term is related with the amount of energy irreversibly removed from the wall. In the particular problem under consideration here, the order of the damping coefficient is estimated to be around ![]() $\unicode{x1D4B9} \sim 10^{-2}$ (Fiford & Bilston Reference Fiford and Bilston2005). Figure 11 shows the stabilizing effect of damping on the growth rate
$\unicode{x1D4B9} \sim 10^{-2}$ (Fiford & Bilston Reference Fiford and Bilston2005). Figure 11 shows the stabilizing effect of damping on the growth rate ![]() $|\mu |$ of the perturbation (conditions similar to those of figure 4). Note that, the additional damping only introduces little variations in the Floquet growth rate
$|\mu |$ of the perturbation (conditions similar to those of figure 4). Note that, the additional damping only introduces little variations in the Floquet growth rate ![]() $|\mu |$ and the critical Reynolds number
$|\mu |$ and the critical Reynolds number ![]() ${ {Re}}_{cr}$, the most unstable wavelength remaining unchanged with respect to the undamped case.
${ {Re}}_{cr}$, the most unstable wavelength remaining unchanged with respect to the undamped case.

Figure 11. Floquet growth rate ![]() $|\mu |$ as a function of the perturbation wavenumber
$|\mu |$ as a function of the perturbation wavenumber ![]() $k$, for
$k$, for ![]() ${ {Re}} = 26$, and
${ {Re}} = 26$, and ![]() $\mathcal {K} = 1$,
$\mathcal {K} = 1$, ![]() $H_1 = H_2 = \infty$, when, on top of the spring stiffness, a damping term is included in the fluid–wall interaction model, for three values of the corresponding dimensionless damping coefficient,
$H_1 = H_2 = \infty$, when, on top of the spring stiffness, a damping term is included in the fluid–wall interaction model, for three values of the corresponding dimensionless damping coefficient, ![]() $\unicode{x1D4B9} = 0$,
$\unicode{x1D4B9} = 0$, ![]() $\unicode{x1D4B9} = 0.02$,
$\unicode{x1D4B9} = 0.02$, ![]() $\unicode{x1D4B9} = 0.04$.
$\unicode{x1D4B9} = 0.04$.
5. Concluding remarks
We have investigated the stability of the fluid–structure interaction problem constituted by two layers of a fluid undergoing an oscillatory motion parallel to the compliant wall that separates them. The study of this canonical configuration is inspired by the cerebrospinal fluid flow occurring in hydromyelia/syringomyelia, a pathology of the central nervous system characterized by the accumulation of fluid within the spinal cord, and its aim is to shed light on the underlying mechanical processes. The problem is governed by the Navier–Stokes equations for a Newtonian, incompressible, fluid, together with a constitutive equation for the compliant solid, for which a spring-backed plate equation was used, only accounting for the stiffness ![]() $\mathcal {K}$ and assuming wall-normal deformations. We investigated the linear stability of the problem by means of a Floquet analysis, focusing on the effect of the different control parameters of the problem, namely the dimensionless fluid layer widths,
$\mathcal {K}$ and assuming wall-normal deformations. We investigated the linear stability of the problem by means of a Floquet analysis, focusing on the effect of the different control parameters of the problem, namely the dimensionless fluid layer widths, ![]() $H_1$ and
$H_1$ and ![]() $H_2$, the Reynolds number,
$H_2$, the Reynolds number, ![]() ${ {Re}}$, and the dimensionless wall stiffness,
${ {Re}}$, and the dimensionless wall stiffness, ![]() $\mathcal {K}$.
$\mathcal {K}$.
Around criticality, i.e. when the absolute value of the Floquet multiplier of the most unstable mode crosses the unit circle, it was found that the perturbations of the flow field oscillate synchronous with the base flow. The associated dimensionless perturbation wavenumber ![]() $k$ is of order unity, or, in other words, the spatially periodic deformations of the separating wall have a length
$k$ is of order unity, or, in other words, the spatially periodic deformations of the separating wall have a length ![]() $2{\rm \pi} /k^\ast$ that is of the order of the stroke length
$2{\rm \pi} /k^\ast$ that is of the order of the stroke length ![]() $l^{\ast }$ of the oscillatory fluid motion. The exact value of that wavenumber depends strongly on the wall stiffness
$l^{\ast }$ of the oscillatory fluid motion. The exact value of that wavenumber depends strongly on the wall stiffness ![]() $\mathcal {K}$, as does the critical Reynolds number
$\mathcal {K}$, as does the critical Reynolds number ![]() ${ {Re}}_{cr}$, underscoring the role that
${ {Re}}_{cr}$, underscoring the role that ![]() $\mathcal {K}$ plays as a reduced velocity, comparing the characteristic time of the spring-induced transverse motion with the longitudinal fluid oscillation period. Our results also reveal that reducing the channel widths has a stabilizing effect, i.e. a larger Reynolds number is necessary to trigger the onset of instability over the entire range of perturbation wavenumbers herein considered. In particular, such stabilizing effect has been found to become stronger as the fluid layers become thinner. The latter stems from the attenuation of the velocity perturbation close to the lateral rigid walls.
$\mathcal {K}$ plays as a reduced velocity, comparing the characteristic time of the spring-induced transverse motion with the longitudinal fluid oscillation period. Our results also reveal that reducing the channel widths has a stabilizing effect, i.e. a larger Reynolds number is necessary to trigger the onset of instability over the entire range of perturbation wavenumbers herein considered. In particular, such stabilizing effect has been found to become stronger as the fluid layers become thinner. The latter stems from the attenuation of the velocity perturbation close to the lateral rigid walls.
The present work constitutes an initial step in understanding the complex fluid–structure interactions encountered in syringomyelia as self-induced perturbations of the flow. It adds a different approach to previous modelling efforts found in the syringomyelia corpus (e.g. Bertram, Brodbelt & Stoodley Reference Bertram, Brodbelt and Stoodley2005; Bertram & Heil Reference Bertram and Heil2016; Heil & Bertram Reference Heil and Bertram2016). In the case studied here, it is encouraging that we find the most unstable wavelengths to be approximately ![]() $2{\rm \pi} /1.5 \simeq 4$ times the stroke length
$2{\rm \pi} /1.5 \simeq 4$ times the stroke length ![]() $l^{\ast }$, which, with
$l^{\ast }$, which, with ![]() $l_{CSF}^{\ast } \simeq 1 \, \textrm {cm}$ in the spinal canal, yields
$l_{CSF}^{\ast } \simeq 1 \, \textrm {cm}$ in the spinal canal, yields ![]() $4\,\textrm {cm}$, comparable to the size of fluid accumulation. This may suggest that syrinx sizes lie in the range in which optimal fluid–structure interaction is achieved, and in which the motion of the intrasyringal fluid is most easily coupled with that of the cerebrospinal fluid surrounding the spinal cord. Future efforts will be focused on the validation of the results using laboratory experiments and direct numerical simulations.
$4\,\textrm {cm}$, comparable to the size of fluid accumulation. This may suggest that syrinx sizes lie in the range in which optimal fluid–structure interaction is achieved, and in which the motion of the intrasyringal fluid is most easily coupled with that of the cerebrospinal fluid surrounding the spinal cord. Future efforts will be focused on the validation of the results using laboratory experiments and direct numerical simulations.
Funding
This work was supported by the coordinated project, PID2020-115961RB-C31, PID2020-115961RB-C32 and PID2020-115961RA-C33, financed by MCIN/AEI/10.13039/501100011033 and by the Junta de Andalucía and European Funds, project no. P18-FR-4619. Funding for open access charge provided by Universidad de Granada.
Declaration of interests
The authors report no conflict of interest.