Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-07-02T20:03:52.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Flexible ring flapping in a uniform flow

Published online by Cambridge University Press:  02 August 2012

Boyoung Kim ,
Wei-Xi Huang ,
Soo Jai Shin  and
Hyung Jin Sung
Boyoung Kim
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 305-701, Korea
Wei-Xi Huang
Affiliation:
Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China
Soo Jai Shin
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 305-701, Korea
Hyung Jin Sung*
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 305-701, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An improved version of the immersed boundary (IB) method for simulating an initially circular or elliptic flexible ring pinned at one point in a uniform flow has been developed. The boundary of the ring consists of a flexible filament with tension and bending stiffness. A penalty method derived from fluid compressibility was used to ensure the conservation of the internal volume of the flexible ring. At 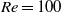, two different flapping modes were identified by varying the tension coefficient for a fixed bending stiffness, or by changing the bending coefficient for a fixed tension coefficient. The optimal tension and bending coefficients that minimize the drag force of the flexible ring were found. Visualization of the vorticity field showed that the two flapping modes correspond to different vortex shedding patterns. We observed the hysteresis property of the flexible ring, which exhibits bistable states over a range of flow velocities depending on the initial inclination angle, i.e. one is a stationary stable state and the other a self-sustained periodically flapping state. The Reynolds number range of the bistability region and the flapping amplitude were determined for various aspect ratios 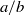. For 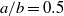, the hysteresis region arises at the highest Reynolds number and the flapping amplitude in the self-sustained flapping state is minimized. A new bistability phenomenon was observed: for certain aspect ratios, two periodically flapping states coexist with different amplitudes in a particular Reynolds number range, instead of the presence of a stationary stable state and a periodically flapping state.

JFM classification

Flow Control: Drag reduction Aerodynamics: Flow-structure interactions Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 129 - 149
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alben, S. & Shelley, M. J. 2008 Flapping states of a flag in an inviscid fluid: bistability and the transition to chaos. Phys. Rev. Lett. 100, 074301.CrossRefGoogle Scholar
2. Bailey, H. 2000 Motion of a hanging chain after the free end is given an initial velocity. Am. J. Phys. 68, 764–767.CrossRefGoogle Scholar
3. Belmonte, A., Shelley, M. J., Eldakar, S. T. & Wiggins, C. H. 2001 Dynamic patterns and self-knotting of a driven hanging chain. Phys. Rev. Lett. 87, 114301.CrossRefGoogle ScholarPubMed
4. Connell, B. S. H. & Yue, D. K. P. 2007 Flapping dynamics of a flag in a uniform stream. J. Fluid Mech. 581, 33–67.CrossRefGoogle Scholar
5. Cortez, R. & Minion, M. 2000 The blob projection method for immersed boundary problems. J. Comput. Phys. 161, 428–453.CrossRefGoogle Scholar
6. Cortez, R., Peskin, C. S., Stockie, J. M. & Varela, D. 2004 Parametric resonance in immersed elastic boundaries. SIAM J. Appl. Maths 65, 494–520.CrossRefGoogle Scholar
7. Eloy, C., Lagrange, R., Souilliez, C. & Schouveiler, L. 2008 Aeroelastic instability of cantilevered flexible plates in uniform flow. J. Fluid Mech. 611, 97–106.CrossRefGoogle Scholar
8. Farnell, D. J. J., David, T. & Barton, D. C. 2004 Numerical simulations of a filament in a flowing soap film. Intl J. Numer. Meth. Fluids 44, 313–330.CrossRefGoogle Scholar
9. Fish, F. E. & Lauder, G. V. 2006 Passive and active flow control by swimming fishes and mammals. Annu. Rev. Fluid Mech. 38, 193–224.CrossRefGoogle Scholar
10. Glowinski, R., Pana, T.-W., Hesla, T. I. & Joseph, D. D. 1999 A distributed Lagrange multiplier/fictitious domain method for particulate flows. Intl J. Multiphase Flow 25, 755–794.CrossRefGoogle Scholar
11. Goldstein, D., Handler, R. & Sirovich, L. 1993 Modeling a no-slip flow boundary with an external force field. J. Comput. Phys 105, 354–366.CrossRefGoogle Scholar
12. Huang, W.-X., Shin, S. J. & Sung, H. J. 2007 Simulation of flexible filaments in a uniform flow by the immersed boundary method. J. Comput. Phys. 226, 2206–2228.CrossRefGoogle Scholar
13. Huber, G. 2000 Swimming in flat sea. Nature 408, 777–778.CrossRefGoogle Scholar
14. Jung, S., Mareck, K., Shelley, M. & Zhang, J. 2006 Dynamics of a deformable body in a fast flowing soap film. Phys. Rev. Lett. 97, 134502.CrossRefGoogle Scholar
15. Kim, K., Baek, S.-J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38, 125–138.CrossRefGoogle Scholar
16. Kim, Y. & Peskin, C. S. 2007 Penalty immersed boundary method for an elastic boundary with mass. Phys. Fluids 19, 053103.CrossRefGoogle Scholar
17. Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Course of Theoretical Physics , vol. 6. Butterworth-Heinemann.Google Scholar
18. Li, Z. & Lai, M.-C. 2001 The immersed interface method for the Navier–Stokes equations with singular forces. J. Comput. Phys. 171, 822–842.CrossRefGoogle Scholar
19. Liao, J. C., Beal, D. N., Lauder, G. V. & Triantafyllou, M. S. 2003 Fish exploiting vortices decrease muscle activity. Science 302, 1566–1569.CrossRefGoogle ScholarPubMed
20. Müller, U. K. 2003 Fish ’n flag. Science 302, 1511–1512.CrossRefGoogle ScholarPubMed
21. Peng, Z., Asaro, R. J. & Zhu, Q. 2010 Multiscale simulation of erythrocyte membrane. Phys. Rev. E 81, 031904.CrossRefGoogle Scholar
22. Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.CrossRefGoogle Scholar
23. Peskin, C. S. & Printz, B. F. 2002 Improved volume conservation in the computation of flows with immersed elastic boundaries. J. Comput. Phys. 105, 33–46.CrossRefGoogle Scholar
24. Qi, D. 2007 A new method for direct simulations of flexible filament suspensions in non-zero Reynolds number flows. Intl J. Numer. Meth. Fluids 54, 103–118.CrossRefGoogle Scholar
25. Shin, S. J., Huang, W.-X. & Sung, H. J. 2008 Assessment of regularized delta functions and feedback forcing schemes for an immersed boundary method. Intl J. Numer. Meth. Fluids 58, 263–286.CrossRefGoogle Scholar
26. Shelley, M. J., Vandenberghe, N. & Zhang, J. 2005 Heavy flags undergo spontaneous oscillations in flowing water. Phys. Rev. Lett. 94, 094302.CrossRefGoogle ScholarPubMed
27. Shoele, K. & Zhu, Q. 2010 Flow-induced vibrations of a deformable ring. J. Fluid Mech. 650, 343–362.CrossRefGoogle Scholar
28. Thess, A., Zikanov, O. & Nepomnyashchy, A. 1999 Finite-time singularity in the vortex dynamics of a string. Phys. Rev. E 59, 3637–3640.CrossRefGoogle Scholar
29. Tornberg, A.-K. & Shelley, M. J. 2004 Simulating the dynamics and interactions of flexible fibres in Stokes flows. J. Comput. Phys. 196, 8–40.CrossRefGoogle Scholar
30. Uhlmann, M. 2006 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209, 448–476.CrossRefGoogle Scholar
31. Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar
32. Yu, Z. 2005 A DLM/FD method for fluid/flexible-body interactions. J. Comput. Phys. 207, 1–27.CrossRefGoogle Scholar
33. Zhang, J., Childress, S., Libchaber, A. & Shelley, M. 2000 Flexible filaments in a flowing soap film as a model for one-dimensional flags in a two-dimensional wind. Nature 408, 835–839.CrossRefGoogle Scholar
34. Zhang, L. J & Eldredge, J. D. 2009 A viscous vortex particle method for deforming bodies with application to biolocomotion. Intl J. Numer. Meth. Fluids 59, 1299–1320.CrossRefGoogle Scholar
35. Zhu, L. & Peskin, C. S. 2002 Simulation of a flapping flexible filament in a flowing soap film by the immersed boundary method. J. Comput. Phys. 179, 452–468.CrossRefGoogle Scholar
36. Zhu, L. & Peskin, C. S. 2003 Interaction of two flapping filaments in a flowing soap film. Phys. Fluids 15, 1954–1960.CrossRefGoogle Scholar