Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T06:51:44.254Z Has data issue: false hasContentIssue false
  • English
  • Français

Flame edge structures and dynamics in planar turbulent non-premixed inclined slot-jet flames impinging at a wall

Published online by Cambridge University Press:  15 June 2021

Guo Chen ,
Haiou Wang Open the ORCID record for Haiou Wang [Opens in a new window] ,
Kun Luo Open the ORCID record for Kun Luo [Opens in a new window]  and
Jianren Fan Open the ORCID record for Jianren Fan [Opens in a new window]
Guo Chen
Affiliation:
State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou310027, PR China
Haiou Wang*
Affiliation:
State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou310027, PR China
Kun Luo
Affiliation:
State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou310027, PR China
Jianren Fan
Affiliation:
State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou310027, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

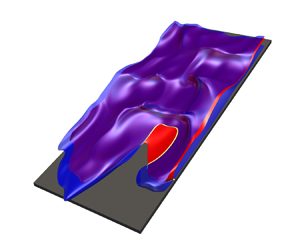
The present paper focuses on the structures and dynamics of flame edges in planar turbulent non-premixed flames bounded with a wall using direct numerical simulation (DNS). The global quenching behaviour was first examined and the flame edges were identified based on the intersections of mixture fraction and OH mass fraction iso-surfaces. For the upper branch of the planar jet flame, it is observed that the structures of flame edges change from tribrachial to monobrachial with increasing scalar dissipation rate. The flame edge speed is negatively correlated with the scalar dissipation rate in regions away from the wall, highlighting the role of turbulent mixing on the flame edge dynamics. During flame–wall interactions, the propagation speed of flame edges is mainly affected by the projection of edge flame normal in the wall-normal direction, i.e. $\boldsymbol {N}_{Z}\boldsymbol {\cdot }\boldsymbol {N}_{wall}$. In particular, the propagation speed increases with increasing $\boldsymbol {N}_{Z}\boldsymbol {\cdot }\boldsymbol {N}_{wall}$ in the near-wall region. The interactions of flame edges and turbulence bounded with a wall are characterized by the alignment between edge flame normal and principal strain rates. The normal of quenching edges has a tendency to align with the most extensive strain rate $\boldsymbol {e}_{1}$ in regions where the heat-release-induced dilatation is dominant over turbulent strain. In contrast, when the heat loss by cold wall effect is large enough to counteract the heat release induced by chemical reactions, turbulent strain is prevalent and the edge flame normal of the quenching edges preferentially aligns with the most compressive strain rate $\boldsymbol {e}_{3}$.

JFM classification

Reacting Flows: Combustion Reacting Flows: Flames Reacting Flows: Turbulent reacting flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , A43
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Amantini, G., Frank, J.H., Bennett, B.A.V., Smooke, M.D. & Gomez, A. 2007 Comprehensive study of the evolution of an annular edge flame during extinction and reignition of a counterflow diffusion flame perturbed by vortices. Combust. Flame 150, 292–319.CrossRefGoogle Scholar
Ashurst, W.T., Kerstein, A.R., Kerr, R.M. & Gibson, C.H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343–2353.CrossRefGoogle Scholar
Bilger, R.W. 1976 The structure of diffusion flames. Combust. Sci. Technol. 13, 155–170.CrossRefGoogle Scholar
Boust, B., Sotton, J., Labuda, S.A. & Bellenoue, M. 2007 A thermal formulation for single-wall quenching of transient laminar flames. Combust. Flame 149, 286–294.CrossRefGoogle Scholar
Bruneaux, G., Akselvoll, K., Poinsot, T. & Ferziger, J.H. 1996 Flame-wall interaction simulation in a turbulent channel flow. Combust. Flame 107, 27–44.CrossRefGoogle Scholar
Buckmaster, J. 2002 Edge-flames. Prog. Energy Combust. Sci. 28, 435–475.CrossRefGoogle Scholar
Cha, M.S. & Ronney, P.D. 2006 Propagation rates of nonpremixed edge flames. Combust. Flame 146, 312–328.CrossRefGoogle Scholar
Chakraborty, N. & Mastorakos, E. 2006 Numerical investigation of edge flame propagation characteristics in turbulent mixing layers. Phys. Fluids 18, 105103.CrossRefGoogle Scholar
Chakraborty, N. & Swaminathan, N. 2007 Influence of the Damköhler number on turbulence-scalar interaction in premixed flames. I. Physical insight. Phys. Fluids 19, 045103.CrossRefGoogle Scholar
Chao, B.H., Law, C.K. & T'ien, J.S. 1991 Structure and extinction of diffusion flames with flame radiation. Symp. (Intl) Combust. 23, 523–531.CrossRefGoogle Scholar
Chen, J.H., et al. 2009 Terascale direct numerical simulations of turbulent combustion using S3D. Comput. Sci. Disc. 2, 015001.CrossRefGoogle Scholar
Chung, S.H. 2007 Stabilization, propagation and instability of tribrachial triple flames. Proc. Combust. Inst. 31, 877–892.CrossRefGoogle Scholar
Cifuentes, L., Dopazo, C., Martin, J. & Jimenez, C. 2014 Local flow topologies and scalar structures in a turbulent premixed flame. Phys. Fluids 26, 065108.CrossRefGoogle Scholar
Daou, J. & Liñán, A. 1998 The role of unequal diffusivities in ignition and extinction fronts in strained mixing layers. Combust. Theor. Model. 2, 449–477.CrossRefGoogle Scholar
Dold, J.W. 1989 Flame propagation in a nonuniform mixture: analysis of a slowly varying triple flame. Combust. Flame 76, 71–88.CrossRefGoogle Scholar
Domingo, P. & Vervisch, L. 1996 Triple flames and partially premixed combustion in autoignition of non-premixed turbulent mixtures. Symp. (Intl) Combust. 26, 233–240.CrossRefGoogle Scholar
Dreizler, A. & Böhm, B. 2015 Advanced laser diagnostics for an improved understanding of premixed flame-wall interactions. Proc. Combust. Inst. 35, 37–64.CrossRefGoogle Scholar
Echekki, T. & Chen, J.H. 1998 Structure and propagation of methanol–air triple flames. Combust. Flame 114, 231–245.CrossRefGoogle Scholar
Favier, V. & Vervisch, L. 2001 Edge flames and partially premixed combustion in diffusion flame quenching. Combust. Flame 125, 788–803.CrossRefGoogle Scholar
Gruber, A., Sankaran, R., Hawkes, E.R. & Chen, J.H. 2010 Turbulent flame–wall interaction: a direct numerical simulation study. J. Fluid Mech. 658, 5–32.CrossRefGoogle Scholar
Hamlington, P.E., Poludnenko, A.Y. & Oran, E.S. 2011 Interactions between turbulence and flames in premixed reacting flows. Phys. Fluids 23, 125111.CrossRefGoogle Scholar
Hartley, L.J. & Dold, J.W. 1991 Flame propagation in a nonuniform mixture: analysis of a propagating triple-flame. Combust. Sci. Technol. 80, 23–46.CrossRefGoogle Scholar
Hartung, G., Hult, J., Kaminski, C.F., Rogerson, J.W. & Swaminathan, N. 2008 Effect of heat release on turbulence and scalar-turbulence interaction in premixed combustion. Phys. Fluids 20, 035110.CrossRefGoogle Scholar
Hasselbrink, E.F. Jr. & Mungal, M.G. 1998 Characteristics of the velocity field near the instantaneous base of lifted non-premixed turbulent jet flames. Symp. (Intl) Combust. 27, 867–873.CrossRefGoogle Scholar
Hawkes, E.R., Chatakonda, O., Kolla, H., Kerstein, A.R. & Chen, J.H. 2012 A petascale direct numerical simulation study of the modelling of flame wrinkling for large-eddy simulations in intense turbulence. Combust. Flame 159, 2690–2703.CrossRefGoogle Scholar
Hawkes, E.R., Sankaran, R. & Chen, J.H. 2007 a Reignition dynamics in massively parallel direct numerical simulations of CO/H$_2$ jet flames. Proc. Aust. Fluid Mech. Conf. 16, 1271–1274.Google Scholar
Hawkes, E.R., Sankaran, R., Sutherland, J.C. & Chen, J.H. 2007 b Scalar mixing in direct numerical simulations of temporally evolving plane jet flames with skeletal CO/H$_2$ kinetics. Proc. Combust. Inst. 31, 1633–1640.CrossRefGoogle Scholar
Hesse, H., Chakraborty, N. & Mastorakos, E. 2009 The effects of the Lewis number of the fuel on the displacement speed of edge flames in igniting turbulent mixing layers. Proc. Combust. Inst. 32, 1399–1407.CrossRefGoogle Scholar
Hewson, J.C. & Kerstein, A.R. 2002 Local extinction and reignition in nonpremixed turbulent CO/H$_2$/N$_2$ jet flames. Combust. Sci. Technol. 174, 35–66.CrossRefGoogle Scholar
Im, H.G. & Chen, J.H. 1999 Structure and propagation of triple flames in partially premixed hydrogen–air mixtures. Combust. Flame 119, 436–454.CrossRefGoogle Scholar
Im, H.G. & Chen, J.H. 2001 Effects of flow strain on triple flame propagation. Combust. Flame 126, 1384–1392.CrossRefGoogle Scholar
Jainski, C., Rißmann, M., Böhm, B. & Dreizler, A. 2017 Experimental investigation of flame surface density and mean reaction rate during flame–wall interaction. Proc. Combust. Inst. 36, 1827–1834.CrossRefGoogle Scholar
Juddoo, M. & Masri, A.R. 2011 High-speed OH-PLIF imaging of extinction and re-ignition in non-premixed flames with various levels of oxygenation. Combust. Flame 158, 902–914.CrossRefGoogle Scholar
Karami, S., Hawkes, E.R., Talei, M. & Chen, J.H. 2015 Mechanisms of flame stabilisation at low lifted height in a turbulent lifted slot-jet flame. J. Fluid Mech. 777, 633–689.CrossRefGoogle Scholar
Karami, S., Hawkes, E.R., Talei, M. & Chen, J.H. 2016 Edge flame structure in a turbulent lifted flame: A direct numerical simulation study. Combust. Flame 169, 110–128.CrossRefGoogle Scholar
Kee, R.J., Rupley, F.M. & Miller, J.A. 1989 Chemkin-II: A Fortran chemical kinetics package for the analysis of gas-phase chemical kinetics, No. SAND-89-8009, Sandia National Lab., Livermore, CA, USA.CrossRefGoogle Scholar
Kennedy, C.A. & Carpenter, M.H. 1994 Several new numerical methods for compressible shear-layer simulations. Appl. Numer. Math. 14, 397–433.CrossRefGoogle Scholar
Kennedy, C.A., Carpenter, M.H. & Lewis, R.M. 2000 Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Math. 35, 177–219.CrossRefGoogle Scholar
Kerr, R.M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Kim, S.H. & Pitsch, H. 2007 Scalar gradient and small-scale structure in turbulent premixed combustion. Phys. Fluids 19, 115104.CrossRefGoogle Scholar
Kim, N.I., Seo, J.I., Oh, K.C. & Shin, H.D. 2005 Lift-off characteristics of triple flame with concentration gradient. Proc. Combust. Inst. 30, 367–374.CrossRefGoogle Scholar
Ko, Y.S., Chung, T.M. & Chung, S.H. 2002 Characteristics of propagating tribrachial flames in counterflow. KSME Intl J. 16, 1710–1718.CrossRefGoogle Scholar
Mann, M., Jainski, C., Euler, M., Böhm, B. & Dreizler, A. 2014 Transient flame–wall interactions: experimental analysis using spectroscopic temperature and CO concentration measurements. Combust. Flame 161, 2371–2386.CrossRefGoogle Scholar
Mastorakos, E. 2009 Ignition of turbulent non-premixed flames. Prog. Energy Combust. Sci. 35, 57–97.CrossRefGoogle Scholar
Mastorakos, E., Taylor, A.M.K.P. & Whitelaw, J.H. 1992 Extinction and temperature characteristics of turbulent counterflow diffusion flames with partial premixing. Combust. Flame 91, 40–54.CrossRefGoogle Scholar
Narukawa, K., Minamoto, Y., Shimura, M. & Tanahashi, M. 2020 Near-wall flame propagation behaviour with and without surface reactions. Fuel 268, 117216.CrossRefGoogle Scholar
Pantano, C. 2004 Direct simulation of non-premixed flame extinction in a methane–air jet with reduced chemistry. J. Fluid Mech. 514, 231–270.CrossRefGoogle Scholar
Pantano, C. & Pullin, D.I. 2004 A statistical description of turbulent diffusion flame holes. Combust. Flame 137, 295–305.CrossRefGoogle Scholar
Passot, T. & Pouquet, A. 1987 Numerical simulation of compressible homogeneous flows in the turbulent regime. J. Fluid Mech. 181, 441–466.CrossRefGoogle Scholar
Phillips, H. 1965 Flame in a buoyant methane layer. Symp. (Intl) Combust. 10, 1277–1283.CrossRefGoogle Scholar
Pitsch, H. 1998 Flamemaster v3. 3.10: A C++ computer program for 0d combustion and 1d laminar flame calculations. http://www.itv.rwth-aachen.de/en/downloads/flamemaster.Google Scholar
Poinsot, T.J., Haworth, D.C. & Bruneaux, G. 1993 Direct simulation and modeling of flame-wall interaction for premixed turbulent combustion. Combust. Flame 95, 118–132.CrossRefGoogle Scholar
Popp, P. & Baum, M. 1997 Analysis of wall heat fluxes, reaction mechanisms, and unburnt hydrocarbons during the head-on quenching of a laminar methane flame. Combust. Flame 108, 327–348.CrossRefGoogle Scholar
Ruetsch, G.R. & Maxey, M.R. 1991 Small-scale features of vorticity and passive scalar fields in homogeneous isotropic turbulence. Phys. Fluids A 3, 1587–1597.CrossRefGoogle Scholar
Santoro, V.S., Liñán, A. & Gomez, A. 2000 Propagation of edge flames in counterflow mixing layers: experiments and theory. Proc. Combust. Inst. 28, 2039–2046.CrossRefGoogle Scholar
Shay, M.L. & Ronney, P.D. 1998 Nonpremixed edge flames in spatially varying straining flows. Combust. Flame 112, 171–180.CrossRefGoogle Scholar
Song, H., Wang, P., Boles, R.S., Matinyan, D., Prahanphap, H., Piotrowicz, J. & Ronney, P.D. 2017 Effects of mixture fraction on edge-flame propagation speeds. Proc. Combust. Inst. 36, 1403–1409.CrossRefGoogle Scholar
Sponfeldner, T., Boxx, I., Hardalupas, Y., Meier, W. & Taylor, M.K.P. 2015 On the alignment of fluid-dynamic principal strain-rates with the 3D flamelet-normal in a premixed turbulent V-flame. Proc. Combust. Inst. 35, 1269–1276.CrossRefGoogle Scholar
Sripakagorn, P., Mitarai, S., Kosaly, G. & Pitsch, H. 2004 Extinction and reignition in a diffusion flame: a direct numerical simulation study. J. Fluid Mech. 518, 231–259.CrossRefGoogle Scholar
Steinberg, A.M., Boxx, I., Arndt, C.M., Frank, J.H. & Meier, W. 2011 Experimental study of flame-hole reignition mechanisms in a turbulent non-premixed jet flame using sustained multi-kHz PIV and crossed-plane OH PLIF. Proc. Combust. Inst. 33, 1663–1672.CrossRefGoogle Scholar
Steinberg, A.M., Driscoll, J.F. & Swaminathan, N. 2012 Statistics and dynamics of turbulence–flame alignment in premixed combustion. Combust. Flame 159, 2576–2588.CrossRefGoogle Scholar
Su, L.K., Sun, O.S. & Mungal, M.G. 2006 Experimental investigation of stabilization mechanisms in turbulent, lifted jet diffusion flames. Combust. Flame 144, 494–512.CrossRefGoogle Scholar
Swaminathan, N. & Grout, R.W. 2006 Interaction of turbulence and scalar fields in premixed flames. Phys. Fluids 18, 045102.CrossRefGoogle Scholar
Trunk, P.J., Boxx, I., Heeger, C., Meier, W., Böhm, B. & Dreizler, A. 2013 Premixed flame propagation in turbulent flow by means of stereoscopic PIV and dual-plane OH-PLIF at sustained kHz repetition rates. Proc. Combust. Inst. 34, 3565–3572.CrossRefGoogle Scholar
Upatnieks, A., Driscoll, J.F., Rasmussen, C.C. & Ceccio, S.L. 2004 Liftoff of turbulent jet flames–assessment of edge flame and other concepts using cinema-PIV. Combust. Flame 138, 259–272.CrossRefGoogle Scholar
Vlachos, D.G., Schmidt, L.D. & Aris, R. 1994 Ignition and extinction of flames near surfaces: combustion of CH$_4$ in air. AIChE J. 40, 1005–1017.CrossRefGoogle Scholar
Wang, H., Chen, G., Luo, K., Hawkes, E.R., Chen, J.H. & Fan, J. 2021 a Turbulence/flame/wall interactions in non-premixed inclined slot-jet flames impinging at a wall using direct numerical simulation. Proc. Combust. Inst. 38 (2), 2711–2720.CrossRefGoogle Scholar
Wang, L., Hawkes, E.R. & Chen, J.H. 2011 Flame edge statistics in turbulent combustion. Proc. Combust. Inst. 33, 1439–1446.CrossRefGoogle Scholar
Wang, H., Hawkes, E.R. & Chen, J.H. 2016 Turbulence-flame interactions in DNS of a laboratory high Karlovitz premixed turbulent jet flame. Phys. Fluids 28, 095107.CrossRefGoogle Scholar
Wang, H., Hawkes, E.R. & Chen, J.H. 2017 a A direct numerical simulation study of flame structure and stabilization of an experimental high Ka CH$_4$/air premixed jet flame. Combust. Flame 180, 110–123.CrossRefGoogle Scholar
Wang, H., Hawkes, E.R., Chen, J.H., Zhou, B., Li, Z. & Aldén, M. 2017 b Direct numerical simulations of a high Karlovitz number laboratory premixed jet flame—an analysis of flame stretch and flame thickening. J. Fluid Mech. 815, 511–536.CrossRefGoogle Scholar
Wang, H., Hawkes, E.R., Ren, J., Chen, G., Luo, K. & Fan, J. 2021 b 2-D and 3-D measurements of flame stretch and turbulence–flame interactions in turbulent premixed flames using DNS. J. Fluid Mech. 913, A11.CrossRefGoogle Scholar
Wang, Y. & Trouvé, A. 2006 Direct numerical simulation of nonpremixed flame–wall interactions. Combust. Flame 144, 461–475.CrossRefGoogle Scholar
Wang, H., Wang, Z., Luo, K., Hawkes, E.R., Chen, J.H. & Fan, J. 2021 c Direct numerical simulation of turbulent boundary layer premixed combustion under auto-ignitive conditions. Combust. Flame 228, 292–301.CrossRefGoogle Scholar
Westbrook, C.K., Adamczyk, A.A. & Lavoie, G.A. 1981 A numerical study of laminar flame wall quenching. Combust. Flame 40, 81–99.CrossRefGoogle Scholar
Williams, F.A. 1985 Combustion Theory. CRC Press.Google Scholar
Yamashita, H., Shimada, M. & Takeno, T. 1996 A numerical study on flame stability at the transition point of jet diffusion flames. Symp. (Intl) Combust. 26, 27–34.CrossRefGoogle Scholar
Yoo, C.S., Sankaran, R. & Chen, J.H. 2009 Three-dimensional direct numerical simulation of a turbulent lifted hydrogen jet flame in heated coflow: flame stabilization and structure. J. Fluid Mech. 640, 453–481.CrossRefGoogle Scholar
Zhao, P., Wang, L. & Chakraborty, N. 2018 Analysis of the flame–wall interaction in premixed turbulent combustion. J. Fluid Mech. 848, 193–218.CrossRefGoogle Scholar