Article contents
The first open channel for yield-stress fluids in porous media
Published online by Cambridge University Press: 03 February 2021
Abstract
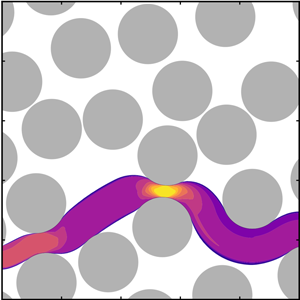
The prediction of the first fluidized path of yield-stress fluids in complex porous media is a challenging yet important task to understand the fundamentals of fluid flow in several industrial and biological processes. In most cases, the conditions that open this first path are known either through experiments or expensive computations. Here, we present a simple network model to predict the first open channel for a yield-stress fluid in a porous medium. For porous media made of non-overlapping discs, we find that the pressure drop  ${\rm \Delta} P_c$ required to open the first channel for a given yield stress
${\rm \Delta} P_c$ required to open the first channel for a given yield stress  $\tau _y$ depends on both the relative discs size
$\tau _y$ depends on both the relative discs size  $R_s$ to the macroscopic length
$R_s$ to the macroscopic length  $L$ of the system and the packing fraction
$L$ of the system and the packing fraction  $\phi$. The non-dimensional pressure gradient
$\phi$. The non-dimensional pressure gradient  ${\rm \Delta} P_c R_s/ \tau _y L$ (i.e. the critical yield number), however, depends on the packing fraction
${\rm \Delta} P_c R_s/ \tau _y L$ (i.e. the critical yield number), however, depends on the packing fraction  $\phi$ only, leading to a mastercurve for all examined ratios of
$\phi$ only, leading to a mastercurve for all examined ratios of  $R_s/L$. In the case of non-overlapping discs, we find
$R_s/L$. In the case of non-overlapping discs, we find  ${\rm \Delta} P_c R_s/ \tau _y L\sim \phi /(1-\phi )$. We also report the statistics on the arclength of the first open path. Finally, we discuss the implication of our results for the design of porous media used in energy storage applications.
${\rm \Delta} P_c R_s/ \tau _y L\sim \phi /(1-\phi )$. We also report the statistics on the arclength of the first open path. Finally, we discuss the implication of our results for the design of porous media used in energy storage applications.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by



