Article contents
Finite-Péclet-number effects on the scaling exponents of high-order passive scalar structure functions
Published online by Cambridge University Press: 26 October 2012
Abstract
The effect of scalar-field (temperature) boundary conditions on the inertial-convective-range scaling exponents of the high-order passive scalar structure functions is studied in the turbulent, heated wake downstream of a circular cylinder. The temperature field is generated two ways: using (i) a heating element embedded within the cylinder that generates the hydrodynamic wake (thus creating a heated cylinder) and (ii) a mandoline (an array of fine, heated wires) installed downstream of the cylinder. The hydrodynamic field is independent of the scalar-field boundary conditions/injection methods, and the same in both flows. Using the two heat injection mechanisms outlined above, the inertial-convective-range scaling exponents of the high-order passive scalar structure functions were measured. It is observed that the different scalar-field boundary conditions yield significantly different scaling exponents (with the magnitude of the difference increasing with structure function order). Moreover, the exponents obtained from the mandoline experiment are smaller than the analogous exponents from the heated cylinder experiment (both of which exhibit a significant departure from the Kolmogorov prediction). Since the observed deviation from the Kolmogorov 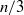 $n/ 3$ prediction arises due to the effects of internal intermittency, the typical interpretation of this result would be that the scalar field downstream of the mandoline is more internally intermittent than that generated by the heated cylinder. However, additional measures of internal intermittency (namely the inertial-convective-range scaling exponents of the mixed, sixth-order, velocity–temperature structure functions and the non-centred autocorrelations of the dissipation rate of scalar variance) suggest that both scalar fields possess similar levels of internal intermittency – a distinctly different conclusion. Examination of the normalized high-order moments reveals that the smaller scaling exponents (of the high-order passive scalar structure functions) obtained for the mandoline experiment arise due to the smaller thermal integral length scale of the flow (i.e. the narrower inertial-convective subrange) and are not solely the result of a more intermittent scalar field. The difference in the passive scalar structure function scaling exponents can therefore be interpreted as an artifact of the different, finite Péclet numbers of the flows under consideration – an effect that is notably less prominent in the other measures of internal intermittency.
$n/ 3$ prediction arises due to the effects of internal intermittency, the typical interpretation of this result would be that the scalar field downstream of the mandoline is more internally intermittent than that generated by the heated cylinder. However, additional measures of internal intermittency (namely the inertial-convective-range scaling exponents of the mixed, sixth-order, velocity–temperature structure functions and the non-centred autocorrelations of the dissipation rate of scalar variance) suggest that both scalar fields possess similar levels of internal intermittency – a distinctly different conclusion. Examination of the normalized high-order moments reveals that the smaller scaling exponents (of the high-order passive scalar structure functions) obtained for the mandoline experiment arise due to the smaller thermal integral length scale of the flow (i.e. the narrower inertial-convective subrange) and are not solely the result of a more intermittent scalar field. The difference in the passive scalar structure function scaling exponents can therefore be interpreted as an artifact of the different, finite Péclet numbers of the flows under consideration – an effect that is notably less prominent in the other measures of internal intermittency.
- Type
- Papers
- Information
- Copyright
- ©2012 Cambridge University Press
References
- 9
- Cited by


