Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T04:17:10.028Z Has data issue: false hasContentIssue false
  • English
  • Français

Feedback loop and upwind-propagating waves in ideally expanded supersonic impinging round jets

Published online by Cambridge University Press:  22 June 2017

Christophe Bogey Open the ORCID record for Christophe Bogey [Opens in a new window]  and
Romain Gojon Open the ORCID record for Romain Gojon [Opens in a new window]
Christophe Bogey*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR CNRS 5509, Ecole Centrale de Lyon, Université de Lyon, 69134 Ecully CEDEX, France
Romain Gojon
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR CNRS 5509, Ecole Centrale de Lyon, Université de Lyon, 69134 Ecully CEDEX, France Department of Mechanics, Royal Institute of Technology (KTH), Linné FLOW Centre, Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The aeroacoustic feedback loop establishing in a supersonic round jet impinging on a flat plate normally has been investigated by combining compressible large-eddy simulations and modelling of that loop. At the exit of a straight pipe nozzle of radius 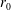$r_{0}$, the jet is ideally expanded, and has a Mach number of 1.5 and a Reynolds number of 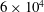$6\times 10^{4}$. Four distances between the nozzle exit and the flat plate, equal to $6r_{0}$, 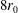$8r_{0}$, 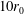$10r_{0}$ and 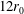$12r_{0}$, have been considered. In this way, the variations of the convection velocity of the shear-layer turbulent structures according to the nozzle-to-plate distance are shown. In the spectra obtained inside and outside of the flow near the nozzle, several tones emerge at Strouhal numbers in agreement with measurements in the literature. At these frequencies, by applying Fourier decomposition to the pressure fields, hydrodynamic-acoustic standing waves containing a whole number of cells between the nozzle and the plate and axisymmetric or helical jet oscillations are found. The tone frequencies and the mode numbers inferred from the standing-wave patterns are in line with the classical feedback-loop model, in which the loop is closed by acoustic waves outside the jet. The axisymmetric or helical nature of the jet oscillations at the tone frequencies is also consistent with a wave analysis using a jet vortex-sheet model, providing the allowable frequency ranges for the upstream-propagating acoustic wave modes of the jet. In particular, the tones are located on the part of the dispersion relations of the modes where these waves have phase and group velocities close to the ambient speed of sound. Based on the observation of the pressure fields and on frequency–wavenumber spectra on the jet axis and in the shear layers, such waves are identified inside the present jets, for the first time to the best of our knowledge, for a supersonic jet flow. This study thus suggests that the feedback loop in ideally expanded impinging jets is completed by these waves.

JFM classification

Acoustics: Acoustics Acoustics: Aeroacoustics Acoustics: Jet noise
Type
Papers
Information
Journal of Fluid Mechanics , Volume 823 , 25 July 2017 , pp. 562 - 591
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berland, J., Bogey, C., Marsden, O. & Bailly, C. 2007 High-order, low dispersive and low dissipative explicit schemes for multiple-scale and boundary problems. J. Comput. Phys. 224 (2), 637–662.CrossRefGoogle Scholar
Berman, C. H. & Williams, J. E. 1970 Instability of a two-dimensional compressible jet. J. Fluid Mech. 42 (01), 151–159.CrossRefGoogle Scholar
Bogey, C.2017 Direct numerical simulation of a temporally-developing subsonic round jet and its sound field. AIAA Paper 2017-0925.CrossRefGoogle Scholar
Bogey, C. & Bailly, C. 2004 A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 194 (1), 194–214.CrossRefGoogle Scholar
Bogey, C. & Bailly, C. 2006 Large eddy simulations of transitional round jets: influence of the Reynolds number on flow development and energy dissipation. Phys. Fluids 18, 065101.CrossRefGoogle Scholar
Bogey, C. & Bailly, C. 2009 Turbulence and energy budget in a self-preserving round jet: direct evaluation using large eddy simulation. J. Fluid Mech. 627, 129–160.CrossRefGoogle Scholar
Bogey, C., de Cacqueray, N. & Bailly, C. 2009 A shock-capturing methodology based on adaptative spatial filtering for high-order non-linear computations. J. Comput. Phys. 228 (5), 1447–1465.CrossRefGoogle Scholar
Bogey, C., de Cacqueray, N. & Bailly, C. 2011a Finite differences for coarse azimuthal discretization and for reduction of effective resolution near origin of cylindrical flow equations. J. Comput. Phys. 230 (4), 1134–1146.CrossRefGoogle Scholar
Bogey, C. & Marsden, O. 2016 Simulations of initially highly disturbed jets with experiment-like exit boundary layers. AIAA J. 54 (2), 1299–2016.CrossRefGoogle Scholar
Bogey, C., Marsden, O. & Bailly, C. 2011b Large-eddy simulation of the flow and acoustic fields of a Reynolds number 105 subsonic jet with tripped exit boundary layers. Phys. Fluids 23, 035104.CrossRefGoogle Scholar
Bogey, C., Marsden, O. & Bailly, C. 2012a Effects of moderate Reynolds numbers on subsonic round jets with highly disturbed nozzle-exit boundary layers. Phys. Fluids 24 (10), 105107.CrossRefGoogle Scholar
Bogey, C., Marsden, O. & Bailly, C. 2012b Influence of initial turbulence level on the flow and sound fields of a subsonic jet at a diameter-based Reynolds number of 105 . J. Fluid Mech. 701, 352–385.CrossRefGoogle Scholar
Brehm, C., Housman, J. A. & Kiris, C. C. 2016 Noise generation mechanisms for a supersonic jet impinging on an inclined plate. J. Fluid Mech. 797, 802–850.CrossRefGoogle Scholar
Brès, G. A., Khalaghi, Y., Ham, F. & Lele, S. K. 2011 Unstructured large eddy simulation technology for aeroacoustics of complex jet flows. In Proceedings of the Inter-Noise 2011 Conference, Institute of Noise Control Engineering, Japan & Acoustical Society of Japan.Google Scholar
Buchmann, N. A., Mitchell, D. M., Ingvorsen, K. M., Honnery, D. R. & Soria, J. 2011 High spatial resolution imaging of a supersonic underexpanded jet impinging on a flat plate. In Proc. 6th Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion, University of New South Wales, Canberra.Google Scholar
de Cacqueray, N., Bogey, C. & Bailly, C. 2011 Investigation of a high-Mach-number overexpanded jet using large-eddy simulation. AIAA J. 49 (10), 2171–2182.CrossRefGoogle Scholar
Dauptain, A., Cuenot, B. & Gicquel, L. Y. M. 2010 Large eddy simulation of stable supersonic jet impinging on flat plate. AIAA J. 48 (10), 2325–2338.CrossRefGoogle Scholar
Dauptain, A., Gicquel, L. Y. M. & Moreau, S. 2012 Large eddy simulation of supersonic impinging jets. AIAA J. 50 (7), 1560–1574.CrossRefGoogle Scholar
Davis, T., Edstrand, A., Alvi, F., Cattafesta, L., Yorita, D. & Asai, K. 2015 Investigation of impinging jet resonant modes using unsteady pressure-sensitive paint measurements. Exp. Fluids 56 (5), 1–13.CrossRefGoogle Scholar
Fauconnier, D., Bogey, C. & Dick, E. 2013 On the performance of relaxation filtering for large-eddy simulation. J. Turbul. 14 (1), 22–49.CrossRefGoogle Scholar
Gojon, R. & Bogey, C. 2017 Flow structure oscillations and tone production in underexpanded impinging round jets. AIAA J. 55 (6), 1792–1804; see also AIAA Paper 2015-2209.CrossRefGoogle Scholar
Gojon, R., Bogey, C. & Marsden, O. 2016 Investigation of tone generation in ideally expanded supersonic planar impinging jets using large-eddy simulation. J. Fluid Mech. 808, 90–115.CrossRefGoogle Scholar
Gutmark, E. & Ho, C.-M. 1983 Preferred modes and the spreading rates of jets. Phys. Fluids 26 (10), 2932–2938.CrossRefGoogle Scholar
Henderson, B., Bridges, J. & Wernet, M. 2005 An experimental study of the oscillatory flow structure of tone-producing supersonic impinging jets. J. Fluid Mech. 542, 115–137.CrossRefGoogle Scholar
Henderson, B. & Powell, A. 1993 Experiments concerning tones produced by an axisymmetric choked jet impinging on flat plates. J. Sound Vib. 168 (2), 307–326.CrossRefGoogle Scholar
Hildebrand, N. & Nichols, J. W.2015 Simulation and stability analysis of a supersonic impinging jet at varying nozzle-to-wall distances. AIAA Paper 2015-2212.CrossRefGoogle Scholar
Ho, C. M. & Nosseir, N. S. 1981 Dynamics of an impinging jet. Part 1. The feedback phenomenon. J. Fluid Mech. 105, 119–142.CrossRefGoogle Scholar
Kim, S. L. & Park, S. O. 2005 Oscillatory behavior of supersonic impinging jet flows. Shock Waves 14 (4), 259–272.CrossRefGoogle Scholar
Kremer, F. & Bogey, C. 2015 Large-eddy simulation of turbulent channel flow using relaxation filtering: resolution requirement and Reynolds number effect. Comput. Fluids 17 (7), 17–28.CrossRefGoogle Scholar
Krothapalli, A. 1985 Discrete tones generated by an impinging underexpanded rectangular jet. AIAA J. 23 (12), 1910–1915.CrossRefGoogle Scholar
Krothapalli, A., Rajkuperan, E., Alvi, F. & Lourenco, L. 1999 Flow field and noise characteristics of a supersonic impinging jet. J. Fluid Mech. 392, 155–181.CrossRefGoogle Scholar
Kuo, C. Y. & Dowling, A. P. 1996 Oscillations of a moderately underexpanded choked jet impinging upon a flat plate. J. Fluid Mech. 315, 267–291.CrossRefGoogle Scholar
Lau, J. C., Morris, P. J. & Fisher, M. J. 1979 Measurements in subsonic and supersonic free jets using a laser velocimeter. J. Fluid Mech. 93 (1), 1–27.CrossRefGoogle Scholar
Lepicovsky, J. & Ahuja, K. K. 1985 Experimental results on edge-tone oscillations in high-speed subsonic jets. AIAA J. 23 (10), 1463–1468.CrossRefGoogle Scholar
Loh, C. Y.2005 Computation of tone noise from supersonic jet impinging on flat plates. NASA/CR-2005-213426, see also AIAA Paper 2005-0418.Google Scholar
Mack, L. M. 1990 On the inviscid acoustic-mode instability of supersonic shear flows. Theor. Comput. Fluid Dyn. 2 (2), 97–123.CrossRefGoogle Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21, 159–199.CrossRefGoogle Scholar
Mitchell, D. M., Honnery, D. R. & Soria, J. 2012 The visualization of the acoustic feedback loop in impinging underexpanded supersonic jet flows using ultra-high frame rate schlieren. J. Vis. 15 (4), 333–341.Google Scholar
Mohseni, K. & Colonius, T. 2000 Numerical treatment of polar coordinate singularities. J. Comput. Phys. 157 (2), 787–795.CrossRefGoogle Scholar
Nichols, J. W. & Lele, S. K. 2011 Global modes and transient response of a cold supersonic jet. J. Fluid Mech. 669, 225–241.CrossRefGoogle Scholar
Nonomura, T., Goto, Y. & Fujii, K. 2011 Aeroacoustic waves generated from a supersonic jet impinging on an inclined flat plate. Intl J. Aeroacoust. 10 (4), 401–426.CrossRefGoogle Scholar
Norum, T. D. 1991 Supersonic rectangular jet impingement noise experiments. AIAA J. 29 (7), 1051–1057.CrossRefGoogle Scholar
Nosseir, N. S. & Ho, C. M. 1982 Dynamics of an impinging jet. Part 2. The noise generation. J. Fluid Mech. 116, 379–391.CrossRefGoogle Scholar
Panda, J., Raman, G. & Zaman, K. B. M. Q.1997 Underexpanded screeching jets from circular, rectangular and elliptic nozzles. AIAA Paper 97-1623.Google Scholar
Powell, A. 1953 On edge tones and associated phenomena. Acta Acust. United Ac. 3, 233–243.Google Scholar
Risborg, A. & Soria, J.2009 High-speed optical measurements of an underexpanded supersonic jet impinging on an inclined plate. In Proc. SPIE 7126, 28th International Congress on High-Speed Imaging and Photonics.CrossRefGoogle Scholar
Rockwell, D. & Naudascher, E. 1978 Review-self-sustaining oscillations of flow past cavities. Trans. ASME J. Fluids Engng 100 (2), 152–165.CrossRefGoogle Scholar
Sabatini, R. & Bailly, C. 2014 Numerical algorithm for computing acoustic and vortical spatial instability waves. AIAA J. 53 (3), 692–702.CrossRefGoogle Scholar
Sakakibara, Y. & Iwamoto, J. 2002 Oscillation of impinging jet with generation of acoustic waves. Intl J. Aeroacoust. 1 (4), 385–402.CrossRefGoogle Scholar
Tam, C. K. W. & Ahuja, K. K. 1990 Theoretical model of discrete tone generation by impinging jets. J. Fluid Mech. 214, 67–87.CrossRefGoogle Scholar
Tam, C. K. W. & Dong, Z. 1994 Wall boundary conditions for high-order finite-difference schemes in computational aeroacoustics. Theor. Comput. Fluid Dyn. 6, 303–322.CrossRefGoogle Scholar
Tam, C. K. W. & Hu, F. Q. 1989 On the three families of instability waves of high-speed jets. J. Fluid Mech. 201, 447–483.CrossRefGoogle Scholar
Tam, C. K. W. & Norum, T. D. 1992 Impingement tones of large aspect ratio supersonic rectangular jets. AIAA J. 30 (2), 304–311.CrossRefGoogle Scholar
Towne, A., Cavalieri, A. V. G, Jordan, P., Colonius, T., Jaunet, V., Schmidt, O. & Brès, G.2016 Trapped acoustic waves in the potential core of subsonic jets. AIAA Paper 2016-2809.CrossRefGoogle Scholar
Umeda, Y., Maeda, H. & Ishii, R. 1987 Discrete tones generated by the impingement of a highspeed jet on a circular cylinder. Phys. Fluids 30 (8), 2380–2388.CrossRefGoogle Scholar
Uzun, A., Kumar, R., Hussaini, M. Y. & Alvi, F. S. 2013 Simulation of tonal noise generation by supersonic impinging jets. AIAA J. 51 (7), 1593–1611.CrossRefGoogle Scholar

Bogey and Gojon supplementary movie

Representation in the $(z,r)$ plane of density in the jet and near the flat plate and of pressure $p-p_0$ for (a) JetL6, (b) JetL8, (c) JetL10 and (d) JetL12. The colour scales range from $1$ to $2$~kg.m$^{-3}$ for density, from blue to red, and from $-5000$ to $5000$~Pa for pressure, from black to white. The nozzle is in black.

Download Bogey and Gojon supplementary movie(Video)
Video 12.1 MB