Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jones, B. Ll.
2014.
Gap Metric Bound Construction From Frequency Response Data.
IFAC Proceedings Volumes,
Vol. 47,
Issue. 3,
p.
9295.
Morgans, Aimee S.
Dahan, Jeremy A.
and
Flinois, Thibault
2014.
Feedback control for reducing the pressure drag of bluff bodies terminated by a backward-facing step.
p.
220.
Lu, Q.
Bowyer, R.
and
Jones, B.Ll.
2015.
Analysis and design of Coleman transform‐based individual pitch controllers for wind‐turbine load reduction.
Wind Energy,
Vol. 18,
Issue. 8,
p.
1451.
Mao, Xuerui
Blackburn, Hugh
and
Sherwin, Spencer
2015.
Optimal suppression of flow perturbations using boundary control.
Computers & Fluids,
Vol. 121,
Issue. ,
p.
133.
Gautier, N.
Aider, J.-L.
Duriez, T.
Noack, B. R.
Segond, M.
and
Abel, M.
2015.
Closed-loop separation control using machine learning.
Journal of Fluid Mechanics,
Vol. 770,
Issue. ,
p.
442.
Oxlade, Anthony R.
Morrison, Jonathan F.
Qubain, Ala
and
Rigas, Georgios
2015.
High-frequency forcing of a turbulent axisymmetric wake.
Journal of Fluid Mechanics,
Vol. 770,
Issue. ,
p.
305.
Mushyam, Aditya
and
Bergada, Josep M
2015.
Active Flow Control on Laminar flow over a Backward facing step.
Journal of Physics: Conference Series,
Vol. 633,
Issue. ,
p.
012110.
Jones, Bryn Ll.
Heins, P. H.
Kerrigan, E. C.
Morrison, J. F.
and
Sharma, A. S.
2015.
Modelling for robust feedback control of fluid flows.
Journal of Fluid Mechanics,
Vol. 769,
Issue. ,
p.
687.
Gautier, N.
and
Aider, J.-L.
2015.
Frequency-lock reactive control of a separated flow enabled by visual sensors.
Experiments in Fluids,
Vol. 56,
Issue. 1,
Zhang, Weiwei
Li, Xintao
Ye, Zhengyin
and
Jiang, Yuewen
2015.
Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 783,
Issue. ,
p.
72.
Brackston, R. D.
García de la Cruz, J. M.
Wynn, A.
Rigas, G.
and
Morrison, J. F.
2016.
Stochastic modelling and feedback control of bistability in a turbulent bluff body wake.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
726.
Flinois, Thibault L. B.
and
Morgans, Aimee S.
2016.
Feedback control of unstable flows: a direct modelling approach using the Eigensystem Realisation Algorithm.
Journal of Fluid Mechanics,
Vol. 793,
Issue. ,
p.
41.
Brackston, Rowan D.
Wynn, Andrew
and
Morrison, Jonathan F.
2016.
Extremum seeking to control the amplitude and frequency of a pulsed jet for bluff body drag reduction.
Experiments in Fluids,
Vol. 57,
Issue. 10,
Sipp, Denis
and
Schmid, Peter J.
2016.
Linear Closed-Loop Control of Fluid Instabilities and Noise-Induced Perturbations: A Review of Approaches and Tools1.
Applied Mechanics Reviews,
Vol. 68,
Issue. 2,
Barros, Diogo
Borée, Jacques
Noack, Bernd R.
Spohn, Andreas
and
Ruiz, Tony
2016.
Bluff body drag manipulation using pulsed jets and Coanda effect.
Journal of Fluid Mechanics,
Vol. 805,
Issue. ,
p.
422.
Atam, Ercan
Mathelin, Lionel
and
Cordier, Laurent
2017.
Identification-Based Closed-Loop Control Strategies for a Cylinder Wake Flow.
IEEE Transactions on Control Systems Technology,
Vol. 25,
Issue. 4,
p.
1488.
Dellar, O. J.
and
Jones, B. Ll
2017.
Dynamically correct formulations of the linearised Navier–Stokes equations.
International Journal for Numerical Methods in Fluids,
Vol. 85,
Issue. 1,
p.
3.
Dalla Longa, L.
Morgans, A. S.
and
Dahan, J. A.
2017.
Reducing the pressure drag of a D-shaped bluff body using linear feedback control.
Theoretical and Computational Fluid Dynamics,
Vol. 31,
Issue. 5-6,
p.
567.
Evstafyeva, O.
Morgans, A. S.
and
Dalla Longa, L.
2017.
Simulation and feedback control of the Ahmed body flow exhibiting symmetry breaking behaviour.
Journal of Fluid Mechanics,
Vol. 817,
Issue. ,
Berk, T.
Medjnoun, T.
and
Ganapathisubramani, B.
2017.
Entrainment effects in periodic forcing of the flow over a backward-facing step.
Physical Review Fluids,
Vol. 2,
Issue. 7,
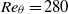 , and a turbulent three-dimensional (3D) flow at
, and a turbulent three-dimensional (3D) flow at 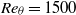 using large-eddy simulation. The control is effected by a full-span slot jet with zero-net-mass-flux, and two jet locations are examined. Linear system identification is performed to characterize the flow response to actuation, used to synthesize a control law. The control strategy is based on the premise that an attenuation of the instantaneous pressure fluctuations on the base of the step should lead to an increase in the time-averaged base pressure. Open-loop harmonic forcing is examined within a broad frequency range for both the 2D and 3D flows, which are found to respond differently to actuation. The controllers based on disturbance attenuation lead to sensible increases in base pressure (up to 70 % in 2D and 20 % in 3D) with higher efficiency than the best results achieved in open-loop. The results support the conjecture about the link between the base pressure fluctuations and mean, although it is shown that such a black-box model approach is not suitable for optimization without further physical insight.
using large-eddy simulation. The control is effected by a full-span slot jet with zero-net-mass-flux, and two jet locations are examined. Linear system identification is performed to characterize the flow response to actuation, used to synthesize a control law. The control strategy is based on the premise that an attenuation of the instantaneous pressure fluctuations on the base of the step should lead to an increase in the time-averaged base pressure. Open-loop harmonic forcing is examined within a broad frequency range for both the 2D and 3D flows, which are found to respond differently to actuation. The controllers based on disturbance attenuation lead to sensible increases in base pressure (up to 70 % in 2D and 20 % in 3D) with higher efficiency than the best results achieved in open-loop. The results support the conjecture about the link between the base pressure fluctuations and mean, although it is shown that such a black-box model approach is not suitable for optimization without further physical insight.