Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T21:33:52.688Z Has data issue: false hasContentIssue false
  • English
  • Français

A falling film on a porous medium

Published online by Cambridge University Press:  25 January 2013

A. Samanta ,
B. Goyeau  and
C. Ruyer-Quil
A. Samanta
Affiliation:
Laboratoire FAST, UPMC Univ. Paris 06, Univ. Paris-Sud, CNRS, UMR CNRS 7608, Bat. 502, Campus Universitaire, F-91405 Orsay, France
B. Goyeau
Affiliation:
Laboratoire EM2C, UPR CNRS 288, Ecole Central Paris, Grande Voie des Vignes, F-92295 Châtenay-Malabry CEDEX, France
C. Ruyer-Quil*
Affiliation:
Laboratoire FAST, UPMC Univ. Paris 06, Univ. Paris-Sud, CNRS, UMR CNRS 7608, Bat. 502, Campus Universitaire, F-91405 Orsay, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A gravity-driven falling film on a saturated porous inclined plane is studied via a continuum approach, where the liquid and porous layers are considered as a single composite layer. Using a weighted residual technique, a two-equation model is derived in terms of the local flow rate $q(x, t)$ and the entire layer thickness 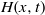$H(x, t)$. Its linear stability analysis has been satisfactorily compared to the results of the Orr–Sommerfeld problem. The principal effect of the porous substrate on the film flow is to displace the liquid–porous interface to an effective liquid–solid interface located at the lower boundary of the upper momentum boundary layer in the porous medium. The stability and dynamics of the film is thus only weakly affected by the presence of a permeable substrate. In both the linear and the nonlinear regimes, the spatial response of a falling film on a porous medium is not very different from that observed on an impermeable inclined wall. However, the wavy motion of the film triggers a significant exchange of mass at the liquid–porous interface.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Geophysical and Geological Flows: Shallow water flows Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 414 - 444
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseenko, S. V., Nakoryakov, V. E. & Pokusaev, B. G. 1994 Wave Flow in Liquid Films, 3rd edn. Begell House.Google Scholar
Beavers, G. S. & Joseph, D. D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207.Google Scholar
Beckermann, C., Ramadhyani, S. & Viskanta, R. 1988 Natural convection in vertical enclosures containing simultaneously fluid and porous layers. J. Fluid Mech. 186, 257–284.Google Scholar
Benjamin, T. B. 1957 Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 2, 554–573.Google Scholar
Bousquet-Melou, P., Goyeau, B., Quintard, M., Fichot, F. & Gobin, D. 2002 Average momentum equation for interdendritic flow in a solidifying columnar mushy zone. Intl J. Heat Mass Transfer 45, 3651–3665.CrossRefGoogle Scholar
Chang, H. C. & Demekhin, E. A. 2002 Complex Wave Dynamics on Thin Films, 1st edn. Elsevier.Google Scholar
Chang, H.-C., Demekhin, E. A. & Kopelevitch, D. I. 1993 Nonlinear evolution of waves on a vertically falling film. J. Fluid Mech. 250, 433–480.CrossRefGoogle Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81, 1131–1198.Google Scholar
Dietze, G. F., Al-Sibai, F. & Kneer, R. 2009 Experimental study of flow separation in laminar falling liquid films. J. Fluid Mech. 637, 73–104.Google Scholar
Dietze, G. F., Leefken, A. & Kneer, R. 2008 Investigation of the backflow phenomenon in falling liquid films. J. Fluid Mech. 595, 435–459.CrossRefGoogle Scholar
Doedel, E. J., Champneys, A. R., Fairgrieve, T. F., Kuznetsov, Y. A., Sandstede, B. & Wang, X.-J. 2007 Auto07: continuation and bifurcation software for ordinary differential equations. Tech. Rep. Department of Computer Science, Concordia University, Montreal, Canada (available from ftp.cs.concordia.ca in directory pub/doedel/auto).Google Scholar
Goyeau, B., Lhuillier, D., Gobin, D. & Velarde, M. G. 2003 Momentum transport at a fluid–porous interface. Intl J. Heat Mass Transfer 46, 4071–4081.Google Scholar
Guyon, E., Hulin, J.-P., Petit, L. & Mitescu, C. 2001 Physical Hydrodynamics, 1st edn. Oxford University Press.CrossRefGoogle Scholar
Hirata, S. C., Goyeau, B. & Gobin, D. 2009 Stability of thermosolutal natural convection in superposed fluid and porous layers. Trans. Porous Med. 78, 525–536.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2011 Falling Liquid Films, 1st edn. Applied Mathematical Sciences , vol. 176. Springer.Google Scholar
Kapitza, P. L. & Kapitza, S. P. 1949 Wave flow of thin layers of a viscous fluid. Part 3. Experimental study of undulatory flow conditions. In Collected Papers of P. L. Kapitza (1965) (ed. D. T. Haar), pp. 690–709. Pergamon.Google Scholar
Kunugi, T. & Kino, C. 2005 DNS of falling film structure and heat transfer via MARS method. Comput. Struct. 83, 455–462.CrossRefGoogle Scholar
Liu, J. & Gollub, J. 1994 Solitary wave dynamics of film flows. Phys. Fluids 6, 1702–1712.Google Scholar
Liu, J., Paul, J. D. & Gollub, J. P. 1993 Measurements of the primary instabilities of film flows. J. Fluid Mech. 250, 69–101.Google Scholar
Malamataris, N. A., Vlachogiannis, M. & Bontozoglou, V. 2002 Solitary waves on inclined films: flow structure and binary interactions. Phys. Fluids 14 (3), 1082–1094.Google Scholar
Nusselt, W. 1916 Die Oberflächenkondensation des Wasserdampfes. Z. Verein. Deutsch. Ing. 50, 541–546.Google Scholar
Ochoa-Tapia, J. A. & Whitaker, S. 1995 Momentum transfer at the boundary between a porous medium and a homogeneous fluid. Part 1. Theoretical development. Intl J. Heat Mass Transfer 38, 2635–2646.Google Scholar
Ooshida, T. 1999 Surface equation of falling film flows with moderate Reynolds number and large but finite Weber number. Phys. Fluids 11, 3247–3269.Google Scholar
Pascal, J. P. 1999 Linear stability of fluid flow down a porous inclined plane. J. Phys. D Appl. Phys. 32, 417–422.Google Scholar
Pradas, M., Tseluiko, D. & Kalliadasis, S. 2011 Rigorous coherent-structure theory for falling liquid films: viscous dispersion effects on bound-state formation and self-organization. Phys. Fluids 23, 044104.CrossRefGoogle Scholar
Roberts, A. J. 1996 Low-dimensional models of thin film fluid dynamics. Phys. Lett. A 212, 63–71.Google Scholar
Ruyer-Quil, C. & Kalliadasis, S. 2012 Wavy regimes of film flow down a fibre. Phys. Rev. E 85, 046302.Google Scholar
Ruyer-Quil, C. & Manneville, P. 1998 Modeling of film flows down inclined planes. Eur. Phys. J. B 6, 277–292.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15, 357–369.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2005 On the speed of solitary waves running down a vertical wall. J. Fluid Mech. 531, 181–190.Google Scholar
Sadiq, I. M. R. & Usha, R. 2008 Thin Newtonian film flow down a porous inclined plane: stability analysis. Phys. Fluids 20, 022105.Google Scholar
Samanta, A., Ruyer-Quil, C. R. & Goyeau, B. 2011 A falling film down a slippery inclined plane. J. Fluid Mech. 684, 353–383.Google Scholar
Scheid, B., Ruyer-Quil, C. & Manneville, P. 2006 Wave patterns in film flows: modelling and three-dimensional waves. J. Fluid Mech. 562, 183–222.CrossRefGoogle Scholar
Shkadov, V. Ya. 1967 Wave flow regimes of a thin layer of viscous fluid subject to gravity. Izv. Ak. Nauk SSSR, Mekh. Zhidk Gaza 1, 43–51. English translation in Fluid Dyn. 2, 29–34 (1970), Faraday Press.CrossRefGoogle Scholar
Sisoev, G. M. & Shkadov, V. Ya. 1999 A two-parameter manifold of wave solutions to an equation for a falling film of viscous fluid. Dokl. Phys. 44, 454–459.Google Scholar
Thiele, U., Goyeau, B. & Velarde, M. G. 2009 Stability analysis of thin film flow along a heated porous wall. Phys. Fluids 21, 014103.Google Scholar
Thomas, H. A. 1939 The propagation of waves in steep prismatic conduits. In Proceedings of Hydraulics Conference, pp. 214–229. University of Iowa.Google Scholar
Usha, R., Millet, S., BenHadid, H. & Rousset, F. 2011 Shear-thinning film on a porous substrate: stability analysis of a one-sided model. Chem. Engng Sci. 66, 5614–5627.CrossRefGoogle Scholar
Whitaker, S. 1996 The Forchheimer equation: a theoretical development. Trans. Porous Med. 25, 27–61.Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley-Interscience.Google Scholar