1. Batchelor & Nitsche's falling clouds
Nitsche & Batchelor (Reference Nitsche and Batchelor1997) examined the temporal evolution of an initially spherical cloud of particles falling in a quiescent fluid in the Stokes regime. Their questions of interest were as follows: Do particles leave the cloud, and if so, how? What is the lifetime of the cloud as a cohesive entity? Their analysis was substantiated by a numerical simulation of interacting particles (with a maximum particle number of  $N=320$), in which the particles were supposed to act as Stokeslets. This approximation assumed that spherical particles could be treated as point particles that interact with their leading fluid velocity disturbance in Stokes flows, which decays as one over the distance to their centre. The cloud was observed to maintain its initial shape, while particles were observed to leak from its rear in a vertical tail that eventually led to its disintegration.
$N=320$), in which the particles were supposed to act as Stokeslets. This approximation assumed that spherical particles could be treated as point particles that interact with their leading fluid velocity disturbance in Stokes flows, which decays as one over the distance to their centre. The cloud was observed to maintain its initial shape, while particles were observed to leak from its rear in a vertical tail that eventually led to its disintegration.
Notwithstanding the small gravitational slip of the particle phase (Batchelor Reference Batchelor1974; Ekiel-Jeżewska, Metzger & Guazzelli Reference Ekiel-Jeżewska, Metzger and Guazzelli2006), the flow around the suspension cloud is, in fact, related to that of the settling of a spherical drop of heavy fluid in an otherwise lighter fluid as described by Hadamard (Reference Hadamard1911) and Rybczyński (Reference Rybczyński1911). Consequently, the cloud falls like a dense, effective-fluid drop, with no surface tension, at a settling speed  $V_c \sim N V_S a/R$, where
$V_c \sim N V_S a/R$, where  $a$ is the particle radius,
$a$ is the particle radius,  $R$ the cloud radius and
$R$ the cloud radius and  $V_S =2 (\rho _p-\rho _f)a^2 g/9\mu$ is the Stokes velocity of an individual particle of density
$V_S =2 (\rho _p-\rho _f)a^2 g/9\mu$ is the Stokes velocity of an individual particle of density  $\rho _p$ settling in the quiescent fluid of viscosity
$\rho _p$ settling in the quiescent fluid of viscosity  $\mu$ and density
$\mu$ and density  $\rho _f$ under the gravitational acceleration
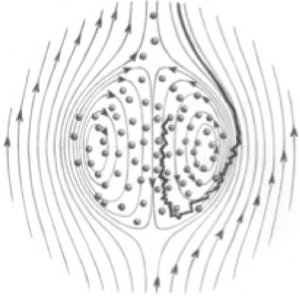
$\rho _f$ under the gravitational acceleration  $g$. In the reference frame of the moving cloud, the particles experience a circular motion along closed toroidal trajectories (the well-known Hadamard–Rybczyński toroidal flow) within the entire volume of the cloud. The hydrodynamic interactions between the particles cause random displacements superposed on this toroidal motion. These random displacements ultimately result in the particle crossing over into the region of the cloud where there is no particle presence, as depicted in figure 1. In this region, the streamlines sweep around the cloud surface and are no longer closed (as they are inside), but extend to infinity. Once particles are swept around to the rear, they fall behind the faster-moving cloud and never catch up again, and thus are lost in the aforementioned tail.
$g$. In the reference frame of the moving cloud, the particles experience a circular motion along closed toroidal trajectories (the well-known Hadamard–Rybczyński toroidal flow) within the entire volume of the cloud. The hydrodynamic interactions between the particles cause random displacements superposed on this toroidal motion. These random displacements ultimately result in the particle crossing over into the region of the cloud where there is no particle presence, as depicted in figure 1. In this region, the streamlines sweep around the cloud surface and are no longer closed (as they are inside), but extend to infinity. Once particles are swept around to the rear, they fall behind the faster-moving cloud and never catch up again, and thus are lost in the aforementioned tail.
Figure 1. A schematic representation of a falling particle cloud illustrating the toroidal circulation of particles within the cloud and the particle leakage in the reference frame of the moving cloud (from a drawing of Sylvie Pic in Guazzelli & Morris Reference Guazzelli and Morris2012).
Having identified the mechanism of the cloud disintegration, Nitsche & Batchelor (Reference Nitsche and Batchelor1997) sought a law governing the rate of particle loss. They proposed that the leakage rate is given by  $-{\rm d}N/{\rm d}t \propto V_c/d$, considering that the rate-determining factor is the fall velocity of the cloud,
$-{\rm d}N/{\rm d}t \propto V_c/d$, considering that the rate-determining factor is the fall velocity of the cloud,  $V_c$, and that the relevant unit of length is the mean particle spacing,
$V_c$, and that the relevant unit of length is the mean particle spacing,  $d= (4{\rm \pi} /3N)^{1/3} R$, as it describes the chaotic displacements of the particles which may result in their escape from the cloud internal circulation. This was confirmed in their simulations, which demonstrated a linear increase in the leakage rate over time.
$d= (4{\rm \pi} /3N)^{1/3} R$, as it describes the chaotic displacements of the particles which may result in their escape from the cloud internal circulation. This was confirmed in their simulations, which demonstrated a linear increase in the leakage rate over time.
2. Later fate of the clouds
The clouds described by Nitsche & Batchelor (Reference Nitsche and Batchelor1997) were composed of a relatively small number of particles ( $20\lesssim N \lesssim 320$) and exhibited a high degree of cohesion until they disintegrated due to the constant loss of particles. In contrast, clouds comprising a larger number of particles (
$20\lesssim N \lesssim 320$) and exhibited a high degree of cohesion until they disintegrated due to the constant loss of particles. In contrast, clouds comprising a larger number of particles ( $N \gtrsim 500$) were subsequently studied and were seen to become unstable (see e.g. Adachi, Kiriyama & Yoshioka Reference Adachi, Kiriyama and Yoshioka1978; Machu et al. Reference Machu, Meile, Nitsche and Schaflinger2001; Metzger, Nicolas & Guazzelli Reference Metzger, Nicolas and Guazzelli2007). These clouds initially remained roughly spherical, with a leakage of particles in a vertical tail, and then slowly evolved into a torus which subsequently broke up into two droplets in a repeating cascade, as shown in figure 2.
$N \gtrsim 500$) were subsequently studied and were seen to become unstable (see e.g. Adachi, Kiriyama & Yoshioka Reference Adachi, Kiriyama and Yoshioka1978; Machu et al. Reference Machu, Meile, Nitsche and Schaflinger2001; Metzger, Nicolas & Guazzelli Reference Metzger, Nicolas and Guazzelli2007). These clouds initially remained roughly spherical, with a leakage of particles in a vertical tail, and then slowly evolved into a torus which subsequently broke up into two droplets in a repeating cascade, as shown in figure 2.
Figure 2. A schematic representation of the evolution of the cloud into a torus and subsequent breakup (the time,  $t^*$, is normalised by the time for the spherical cloud to fall its radius) (from a drawing of Sylvie Pic in Guazzelli & Morris Reference Guazzelli and Morris2012).
$t^*$, is normalised by the time for the spherical cloud to fall its radius) (from a drawing of Sylvie Pic in Guazzelli & Morris Reference Guazzelli and Morris2012).
The leakage rate found by Nitsche & Batchelor (Reference Nitsche and Batchelor1997) was at least confirmed as the cloud remains spherical while falling through the first 10 cloud diameters. At larger times, when the cloud has evolved towards a toroidal shape, the loss slowed down, and a  $t^{-1/3}$ leakage rate was observed (Metzger et al. Reference Metzger, Nicolas and Guazzelli2007). What is more intriguing is the later development that took place long after the early times of cloud evolution studied by Nitsche & Batchelor (Reference Nitsche and Batchelor1997). This process involved the robust evolution of the initial spherical cloud into a torus, followed by its subsequent breakup, which occurs even in the complete absence of inertia and without the need to perturb the initial cloud shape. The previously described leakage of particles from the outer streamlines of the toroidal circulation results in a deficit of particles near the vertical axis in the central region of the cloud, which in turn gives rise to the formation of a torus. The toroidal cloud is then observed to expand and to break into two droplets for a critical horizontal to vertical aspect ratio. While the precise mechanism by which the toroidal cloud expands remains unclear, the breakup of the torus is a consequence of the change in flow configuration created by the particles when the aspect ratio reaches a critical value (Metzger et al. Reference Metzger, Nicolas and Guazzelli2007).
$t^{-1/3}$ leakage rate was observed (Metzger et al. Reference Metzger, Nicolas and Guazzelli2007). What is more intriguing is the later development that took place long after the early times of cloud evolution studied by Nitsche & Batchelor (Reference Nitsche and Batchelor1997). This process involved the robust evolution of the initial spherical cloud into a torus, followed by its subsequent breakup, which occurs even in the complete absence of inertia and without the need to perturb the initial cloud shape. The previously described leakage of particles from the outer streamlines of the toroidal circulation results in a deficit of particles near the vertical axis in the central region of the cloud, which in turn gives rise to the formation of a torus. The toroidal cloud is then observed to expand and to break into two droplets for a critical horizontal to vertical aspect ratio. While the precise mechanism by which the toroidal cloud expands remains unclear, the breakup of the torus is a consequence of the change in flow configuration created by the particles when the aspect ratio reaches a critical value (Metzger et al. Reference Metzger, Nicolas and Guazzelli2007).
The point-particle approach, pioneered by Nitsche & Batchelor (Reference Nitsche and Batchelor1997), has proven to be highly effective in capturing the evolution of the cloud. Subsequent numerical simulations, which have employed a range of varying degrees of sophistication, have been conducted to replicate this evolution (see, for example, one of the latest modelling attempt by Zhan & Wenxiao Reference Zhan and Wenxiao2024). These more evolved simulations capture the multi-body and lubrication effects that are missed in the Stokeslet approximation and are certainly more accurate at modelling more concentrated clouds. However, the primary objective of the simplified Stokeslet simulation is to demonstrate the minimal physics required to describe the long-range hydrodynamic interactions between the particles and to illustrate how the coupling between hydrodynamics and the microscopic arrangement of the particles gives rise to a collective dynamics.
Up to this point, our attention has been directed towards clouds of spherical particles. A comparable evolution and breakup has been observed in clouds of fibres, although at a faster rate due to the self-motion of the anisotropic particles (Park et al. Reference Park, Metzger, Guazzelli and Butler2010).
3. Beyond Stokes flows
In §§ 1 and 2, inertia was ignored. However, in most phenomena involving the dispersion of particles, such as turbidity currents, volcanic clouds, particle sedimentation in river beds or dust particle transport in the atmosphere, the particulate flow is dominated by inertial forces.
As the inertia of the falling cloud is increased, a transition occurs to a regime dominated by macro-scale inertia. This transition happens when the inertia at the scale of the cloud becomes large, which is indicated by the cloud Reynolds number,  $Re_c=\rho _f V_c R/\mu$, reaching a value of approximately one, i.e.
$Re_c=\rho _f V_c R/\mu$, reaching a value of approximately one, i.e.  $Re_c \sim 1$ (Bosse et al. Reference Bosse, Kleiser, Härtel and Meiburg2005). The subsequent transition is toward a micro-scale inertial regime when the inertia at the particle scale becomes important, i.e. when the individual particle wakes interact within the cloud boundaries. In its most basic form, particles interact through their steady Oseen velocity fields within the cloud and the micro-scale inertial regime occurs when the inertial length is of the order of the cloud radius, i.e.
$Re_c \sim 1$ (Bosse et al. Reference Bosse, Kleiser, Härtel and Meiburg2005). The subsequent transition is toward a micro-scale inertial regime when the inertia at the particle scale becomes important, i.e. when the individual particle wakes interact within the cloud boundaries. In its most basic form, particles interact through their steady Oseen velocity fields within the cloud and the micro-scale inertial regime occurs when the inertial length is of the order of the cloud radius, i.e.  $a/Re_a \sim R$, where
$a/Re_a \sim R$, where  $Re_a=\rho _f V_S a/\mu$ is the particle Reynolds number (Subramanian & Koch Reference Subramanian and Koch2008). In both inertial regimes, the cloud deforms into a flat torus that eventually destabilises and breaks up into a number of secondary droplets. However, particle leakage is much weaker if not null. While this evolution resembles that observed in the Stokes regime, the physical mechanisms involved are qualitatively different (Pignatel, Nicolas & Guazzelli Reference Pignatel, Nicolas and Guazzelli2011). In the inertial regimes, the evolution towards a torus shape is due to fluid inflow at the rear of the cloud, which leads to a decrease in particle leakage. The breakup process also differs, occurring at a larger aspect ratio of the torus within the inertial regime.
$Re_a=\rho _f V_S a/\mu$ is the particle Reynolds number (Subramanian & Koch Reference Subramanian and Koch2008). In both inertial regimes, the cloud deforms into a flat torus that eventually destabilises and breaks up into a number of secondary droplets. However, particle leakage is much weaker if not null. While this evolution resembles that observed in the Stokes regime, the physical mechanisms involved are qualitatively different (Pignatel, Nicolas & Guazzelli Reference Pignatel, Nicolas and Guazzelli2011). In the inertial regimes, the evolution towards a torus shape is due to fluid inflow at the rear of the cloud, which leads to a decrease in particle leakage. The breakup process also differs, occurring at a larger aspect ratio of the torus within the inertial regime.
The aforementioned studies consider finite-but-moderate-Reynolds-number clouds. However, there are additional complexities in even larger-Reynolds-number clouds, including turbulent clouds of particles whose behaviour may deviate from a turbulent thermal model due to inertial particulate effects (see e.g. Kriaa et al. Reference Kriaa, Subra, Favier and Le Bars2022). Furthermore, the interactions between particles and flow structures, as well as the collective effects between particles, are also important when particle clouds are settling in a complex flowing fluid rather than a quiescent fluid (see e.g. Marchetti, Bergougnoux & Guazzelli Reference Marchetti, Bergougnoux and Guazzelli2011).
Although these cloud behaviours are considerably more complex than those studied by Nitsche & Batchelor (Reference Nitsche and Batchelor1997), their work evidencing collective effects remains a great source of inspiration.


 $t^*$, is normalised by the time for the spherical cloud to fall its radius) (from a drawing of Sylvie Pic in Guazzelli & Morris 2012).
$t^*$, is normalised by the time for the spherical cloud to fall its radius) (from a drawing of Sylvie Pic in Guazzelli & Morris 2012).
1. Batchelor & Nitsche's falling clouds
Nitsche & Batchelor (Reference Nitsche and Batchelor1997) examined the temporal evolution of an initially spherical cloud of particles falling in a quiescent fluid in the Stokes regime. Their questions of interest were as follows: Do particles leave the cloud, and if so, how? What is the lifetime of the cloud as a cohesive entity? Their analysis was substantiated by a numerical simulation of interacting particles (with a maximum particle number of $N=320$), in which the particles were supposed to act as Stokeslets. This approximation assumed that spherical particles could be treated as point particles that interact with their leading fluid velocity disturbance in Stokes flows, which decays as one over the distance to their centre. The cloud was observed to maintain its initial shape, while particles were observed to leak from its rear in a vertical tail that eventually led to its disintegration.
$N=320$), in which the particles were supposed to act as Stokeslets. This approximation assumed that spherical particles could be treated as point particles that interact with their leading fluid velocity disturbance in Stokes flows, which decays as one over the distance to their centre. The cloud was observed to maintain its initial shape, while particles were observed to leak from its rear in a vertical tail that eventually led to its disintegration.
Notwithstanding the small gravitational slip of the particle phase (Batchelor Reference Batchelor1974; Ekiel-Jeżewska, Metzger & Guazzelli Reference Ekiel-Jeżewska, Metzger and Guazzelli2006), the flow around the suspension cloud is, in fact, related to that of the settling of a spherical drop of heavy fluid in an otherwise lighter fluid as described by Hadamard (Reference Hadamard1911) and Rybczyński (Reference Rybczyński1911). Consequently, the cloud falls like a dense, effective-fluid drop, with no surface tension, at a settling speed $V_c \sim N V_S a/R$, where
$V_c \sim N V_S a/R$, where  $a$ is the particle radius,
$a$ is the particle radius,  $R$ the cloud radius and
$R$ the cloud radius and  $V_S =2 (\rho _p-\rho _f)a^2 g/9\mu$ is the Stokes velocity of an individual particle of density
$V_S =2 (\rho _p-\rho _f)a^2 g/9\mu$ is the Stokes velocity of an individual particle of density  $\rho _p$ settling in the quiescent fluid of viscosity
$\rho _p$ settling in the quiescent fluid of viscosity  $\mu$ and density
$\mu$ and density  $\rho _f$ under the gravitational acceleration
$\rho _f$ under the gravitational acceleration  $g$. In the reference frame of the moving cloud, the particles experience a circular motion along closed toroidal trajectories (the well-known Hadamard–Rybczyński toroidal flow) within the entire volume of the cloud. The hydrodynamic interactions between the particles cause random displacements superposed on this toroidal motion. These random displacements ultimately result in the particle crossing over into the region of the cloud where there is no particle presence, as depicted in figure 1. In this region, the streamlines sweep around the cloud surface and are no longer closed (as they are inside), but extend to infinity. Once particles are swept around to the rear, they fall behind the faster-moving cloud and never catch up again, and thus are lost in the aforementioned tail.
$g$. In the reference frame of the moving cloud, the particles experience a circular motion along closed toroidal trajectories (the well-known Hadamard–Rybczyński toroidal flow) within the entire volume of the cloud. The hydrodynamic interactions between the particles cause random displacements superposed on this toroidal motion. These random displacements ultimately result in the particle crossing over into the region of the cloud where there is no particle presence, as depicted in figure 1. In this region, the streamlines sweep around the cloud surface and are no longer closed (as they are inside), but extend to infinity. Once particles are swept around to the rear, they fall behind the faster-moving cloud and never catch up again, and thus are lost in the aforementioned tail.
Figure 1. A schematic representation of a falling particle cloud illustrating the toroidal circulation of particles within the cloud and the particle leakage in the reference frame of the moving cloud (from a drawing of Sylvie Pic in Guazzelli & Morris Reference Guazzelli and Morris2012).
Having identified the mechanism of the cloud disintegration, Nitsche & Batchelor (Reference Nitsche and Batchelor1997) sought a law governing the rate of particle loss. They proposed that the leakage rate is given by $-{\rm d}N/{\rm d}t \propto V_c/d$, considering that the rate-determining factor is the fall velocity of the cloud,
$-{\rm d}N/{\rm d}t \propto V_c/d$, considering that the rate-determining factor is the fall velocity of the cloud,  $V_c$, and that the relevant unit of length is the mean particle spacing,
$V_c$, and that the relevant unit of length is the mean particle spacing,  $d= (4{\rm \pi} /3N)^{1/3} R$, as it describes the chaotic displacements of the particles which may result in their escape from the cloud internal circulation. This was confirmed in their simulations, which demonstrated a linear increase in the leakage rate over time.
$d= (4{\rm \pi} /3N)^{1/3} R$, as it describes the chaotic displacements of the particles which may result in their escape from the cloud internal circulation. This was confirmed in their simulations, which demonstrated a linear increase in the leakage rate over time.
2. Later fate of the clouds
The clouds described by Nitsche & Batchelor (Reference Nitsche and Batchelor1997) were composed of a relatively small number of particles ( $20\lesssim N \lesssim 320$) and exhibited a high degree of cohesion until they disintegrated due to the constant loss of particles. In contrast, clouds comprising a larger number of particles (
$20\lesssim N \lesssim 320$) and exhibited a high degree of cohesion until they disintegrated due to the constant loss of particles. In contrast, clouds comprising a larger number of particles ( $N \gtrsim 500$) were subsequently studied and were seen to become unstable (see e.g. Adachi, Kiriyama & Yoshioka Reference Adachi, Kiriyama and Yoshioka1978; Machu et al. Reference Machu, Meile, Nitsche and Schaflinger2001; Metzger, Nicolas & Guazzelli Reference Metzger, Nicolas and Guazzelli2007). These clouds initially remained roughly spherical, with a leakage of particles in a vertical tail, and then slowly evolved into a torus which subsequently broke up into two droplets in a repeating cascade, as shown in figure 2.
$N \gtrsim 500$) were subsequently studied and were seen to become unstable (see e.g. Adachi, Kiriyama & Yoshioka Reference Adachi, Kiriyama and Yoshioka1978; Machu et al. Reference Machu, Meile, Nitsche and Schaflinger2001; Metzger, Nicolas & Guazzelli Reference Metzger, Nicolas and Guazzelli2007). These clouds initially remained roughly spherical, with a leakage of particles in a vertical tail, and then slowly evolved into a torus which subsequently broke up into two droplets in a repeating cascade, as shown in figure 2.
Figure 2. A schematic representation of the evolution of the cloud into a torus and subsequent breakup (the time, $t^*$, is normalised by the time for the spherical cloud to fall its radius) (from a drawing of Sylvie Pic in Guazzelli & Morris Reference Guazzelli and Morris2012).
$t^*$, is normalised by the time for the spherical cloud to fall its radius) (from a drawing of Sylvie Pic in Guazzelli & Morris Reference Guazzelli and Morris2012).
The leakage rate found by Nitsche & Batchelor (Reference Nitsche and Batchelor1997) was at least confirmed as the cloud remains spherical while falling through the first 10 cloud diameters. At larger times, when the cloud has evolved towards a toroidal shape, the loss slowed down, and a $t^{-1/3}$ leakage rate was observed (Metzger et al. Reference Metzger, Nicolas and Guazzelli2007). What is more intriguing is the later development that took place long after the early times of cloud evolution studied by Nitsche & Batchelor (Reference Nitsche and Batchelor1997). This process involved the robust evolution of the initial spherical cloud into a torus, followed by its subsequent breakup, which occurs even in the complete absence of inertia and without the need to perturb the initial cloud shape. The previously described leakage of particles from the outer streamlines of the toroidal circulation results in a deficit of particles near the vertical axis in the central region of the cloud, which in turn gives rise to the formation of a torus. The toroidal cloud is then observed to expand and to break into two droplets for a critical horizontal to vertical aspect ratio. While the precise mechanism by which the toroidal cloud expands remains unclear, the breakup of the torus is a consequence of the change in flow configuration created by the particles when the aspect ratio reaches a critical value (Metzger et al. Reference Metzger, Nicolas and Guazzelli2007).
$t^{-1/3}$ leakage rate was observed (Metzger et al. Reference Metzger, Nicolas and Guazzelli2007). What is more intriguing is the later development that took place long after the early times of cloud evolution studied by Nitsche & Batchelor (Reference Nitsche and Batchelor1997). This process involved the robust evolution of the initial spherical cloud into a torus, followed by its subsequent breakup, which occurs even in the complete absence of inertia and without the need to perturb the initial cloud shape. The previously described leakage of particles from the outer streamlines of the toroidal circulation results in a deficit of particles near the vertical axis in the central region of the cloud, which in turn gives rise to the formation of a torus. The toroidal cloud is then observed to expand and to break into two droplets for a critical horizontal to vertical aspect ratio. While the precise mechanism by which the toroidal cloud expands remains unclear, the breakup of the torus is a consequence of the change in flow configuration created by the particles when the aspect ratio reaches a critical value (Metzger et al. Reference Metzger, Nicolas and Guazzelli2007).
The point-particle approach, pioneered by Nitsche & Batchelor (Reference Nitsche and Batchelor1997), has proven to be highly effective in capturing the evolution of the cloud. Subsequent numerical simulations, which have employed a range of varying degrees of sophistication, have been conducted to replicate this evolution (see, for example, one of the latest modelling attempt by Zhan & Wenxiao Reference Zhan and Wenxiao2024). These more evolved simulations capture the multi-body and lubrication effects that are missed in the Stokeslet approximation and are certainly more accurate at modelling more concentrated clouds. However, the primary objective of the simplified Stokeslet simulation is to demonstrate the minimal physics required to describe the long-range hydrodynamic interactions between the particles and to illustrate how the coupling between hydrodynamics and the microscopic arrangement of the particles gives rise to a collective dynamics.
Up to this point, our attention has been directed towards clouds of spherical particles. A comparable evolution and breakup has been observed in clouds of fibres, although at a faster rate due to the self-motion of the anisotropic particles (Park et al. Reference Park, Metzger, Guazzelli and Butler2010).
3. Beyond Stokes flows
In §§ 1 and 2, inertia was ignored. However, in most phenomena involving the dispersion of particles, such as turbidity currents, volcanic clouds, particle sedimentation in river beds or dust particle transport in the atmosphere, the particulate flow is dominated by inertial forces.
As the inertia of the falling cloud is increased, a transition occurs to a regime dominated by macro-scale inertia. This transition happens when the inertia at the scale of the cloud becomes large, which is indicated by the cloud Reynolds number, $Re_c=\rho _f V_c R/\mu$, reaching a value of approximately one, i.e.
$Re_c=\rho _f V_c R/\mu$, reaching a value of approximately one, i.e.  $Re_c \sim 1$ (Bosse et al. Reference Bosse, Kleiser, Härtel and Meiburg2005). The subsequent transition is toward a micro-scale inertial regime when the inertia at the particle scale becomes important, i.e. when the individual particle wakes interact within the cloud boundaries. In its most basic form, particles interact through their steady Oseen velocity fields within the cloud and the micro-scale inertial regime occurs when the inertial length is of the order of the cloud radius, i.e.
$Re_c \sim 1$ (Bosse et al. Reference Bosse, Kleiser, Härtel and Meiburg2005). The subsequent transition is toward a micro-scale inertial regime when the inertia at the particle scale becomes important, i.e. when the individual particle wakes interact within the cloud boundaries. In its most basic form, particles interact through their steady Oseen velocity fields within the cloud and the micro-scale inertial regime occurs when the inertial length is of the order of the cloud radius, i.e.  $a/Re_a \sim R$, where
$a/Re_a \sim R$, where  $Re_a=\rho _f V_S a/\mu$ is the particle Reynolds number (Subramanian & Koch Reference Subramanian and Koch2008). In both inertial regimes, the cloud deforms into a flat torus that eventually destabilises and breaks up into a number of secondary droplets. However, particle leakage is much weaker if not null. While this evolution resembles that observed in the Stokes regime, the physical mechanisms involved are qualitatively different (Pignatel, Nicolas & Guazzelli Reference Pignatel, Nicolas and Guazzelli2011). In the inertial regimes, the evolution towards a torus shape is due to fluid inflow at the rear of the cloud, which leads to a decrease in particle leakage. The breakup process also differs, occurring at a larger aspect ratio of the torus within the inertial regime.
$Re_a=\rho _f V_S a/\mu$ is the particle Reynolds number (Subramanian & Koch Reference Subramanian and Koch2008). In both inertial regimes, the cloud deforms into a flat torus that eventually destabilises and breaks up into a number of secondary droplets. However, particle leakage is much weaker if not null. While this evolution resembles that observed in the Stokes regime, the physical mechanisms involved are qualitatively different (Pignatel, Nicolas & Guazzelli Reference Pignatel, Nicolas and Guazzelli2011). In the inertial regimes, the evolution towards a torus shape is due to fluid inflow at the rear of the cloud, which leads to a decrease in particle leakage. The breakup process also differs, occurring at a larger aspect ratio of the torus within the inertial regime.
The aforementioned studies consider finite-but-moderate-Reynolds-number clouds. However, there are additional complexities in even larger-Reynolds-number clouds, including turbulent clouds of particles whose behaviour may deviate from a turbulent thermal model due to inertial particulate effects (see e.g. Kriaa et al. Reference Kriaa, Subra, Favier and Le Bars2022). Furthermore, the interactions between particles and flow structures, as well as the collective effects between particles, are also important when particle clouds are settling in a complex flowing fluid rather than a quiescent fluid (see e.g. Marchetti, Bergougnoux & Guazzelli Reference Marchetti, Bergougnoux and Guazzelli2011).
Although these cloud behaviours are considerably more complex than those studied by Nitsche & Batchelor (Reference Nitsche and Batchelor1997), their work evidencing collective effects remains a great source of inspiration.
Declaration of interests
The author reports no conflict of interest.