Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T10:40:59.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Extreme-scale motions in turbulent plane Couette flows

Published online by Cambridge University Press:  06 March 2018

Myoungkyu Lee Open the ORCID record for Myoungkyu Lee [Opens in a new window]  and
Robert D. Moser Open the ORCID record for Robert D. Moser [Opens in a new window]
Myoungkyu Lee
Affiliation:
Center for Predictive Engineering and Computational Sciences, Insititute for Computational Engineering and Sciences, The University of Texas at Austin, TX 78712, USA
Robert D. Moser*
Affiliation:
Center for Predictive Engineering and Computational Sciences, Insititute for Computational Engineering and Sciences, The University of Texas at Austin, TX 78712, USA Department of Mechanical Engineering, The University of Texas at Austin, TX 78712, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

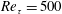We study the large-scale motions in turbulent plane Couette flows at moderate friction Reynolds number up to $Re_{\unicode[STIX]{x1D70F}}=500$. Direct numerical simulation (DNS) domains were as large as 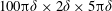$100\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}\times 2\unicode[STIX]{x1D6FF}\times 5\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}$, where 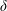$\unicode[STIX]{x1D6FF}$ is half the distance between the walls. The results indicate that there are streamwise vortices filling the space between the walls that remain correlated over distances in the streamwise direction and that increase strongly with the Reynolds number, so that for the largest Reynolds number studied here, they are correlated across the entire 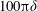$100\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}$ length of the domain. The presence of these very long structures is apparent in the spectra of all three velocity components and the Reynolds stress. In DNS using a smaller domain, the large structures are constrained, eliminating the streamwise variations present in the larger domain. Near the centre of the domain, these large-scale structures contribute as much as half of the Reynolds shear stress.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 128 - 145
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Avsarkisov, V., Hoyas, S., Oberlack, M. & García-Galache, J. P. 2014 Turbulent plane Couette flow at moderately high Reynolds number. J. Fluid Mech. 751, R1.Google Scholar
Barkley, D. & Tuckerman, L. S. 2005 Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 94, 014502.Google Scholar
Barkley, D. & Tuckerman, L. S. 2007 Mean flow of turbulent-laminar patterns in plane Couette flow. J. Fluid Mech. 576, 109–137.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.Google Scholar
Busse, F. H. 1970 Bounds for turbulent shear flow. J. Fluid Mech. 41 (1), 219–240.Google Scholar
Chantry, M., Tuckerman, L. S. & Barkley, D. 2016 Turbulent–laminar patterns in shear flows without walls. J. Fluid Mech. 791, R8.CrossRefGoogle Scholar
Couliou, M. & Monchaux, R. 2015 Large-scale flows in transitional plane Couette flow: a key ingredient of the spot growth mechanism. Phys. Fluids 27, 034101.CrossRefGoogle Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18, 011702.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Johnson, R. W. 2005 Higher order B-spline collocation at the Greville abscissae. Appl. Numer. Maths 52, 63–75.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kitoh, O., Nakabyashi, K. & Nishimura, F. 2005 Experimental study on mean velocity and turbulence characteristics of plane Couette flow: low-Reynolds-number effects and large longitudinal vortical structure. J. Fluid Mech. 539, 199–227.Google Scholar
Kitoh, O. & Umeki, M. 2008 Experimental study on large-scale streak structure in the core region of turbulent plane Couette flow. Phys. Fluids 20 (2), 025107.Google Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.Google Scholar
Lee, M., Malaya, N. & Moser, R. D. 2013 Petascale direct numerical simulation of turbulent channel flow on up to 786K cores. In The International Conference for High Performance Computing, Networking, Storage and Analysis, pp. 1–11. ACM Press.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Lee, M., Ulerich, R., Malaya, N. & Moser, R. D. 2014 Experiences from leadership computing in simulations of turbulent fluid flows. Comput. Sci. Eng. 16 (5), 24–31.Google Scholar
Lee, M. J. & Kim, J. 1991 The structure of turbulence in a simulated plane Couette flow. In Eighth Symposium on Turbulent Shear Flows, Technical University of Munich, pp. 5.3.1–5.3.6.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26, 011702.Google Scholar
Lund, K. O. & Bush, W. B. 1980 Asymptotic analysis of plane turbulent Couette-Poiseuille flows. J. Fluid Mech. 96 (1), 81–104.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Oliver, T. A., Malaya, N., Ulerich, R. & Moser, R. D. 2014 Estimating uncertainties in statistics computed from direct numerical simulation. Phys. Fluids 26, 035101.Google Scholar
Orlandi, P., Bernardini, M. & Pirozzoli, S. 2015 Poiseuille and Couette flows in the transitional and fully turbulent regime. J. Fluid Mech. 770, 424–441.Google Scholar
Papavassiliou, D. V. & Hanratty, T. J. 1997 Interpretation of large-scale structures observed in a turbulent plane Couette flow. Intl J. Heat Fluid Flow 18 (1), 55–69.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2014 Turbulence statistics in Couette flow at high Reynolds number. J. Fluid Mech. 758, 327–343.Google Scholar
Prigent, A., Grégoire, G., Chaté, H. & Dauchot, O. 2003 Long-wavelength modulation of turbulent shear flows. Physica D 174, 100–113.CrossRefGoogle Scholar
Tillmark, N. & Alfredsson, P. H. 1992 Experiments on transition in plane Couette flow. J. Fluid Mech. 235, 89–102.Google Scholar
Tsukahara, T., Kawamura, H. & Shingai, K. 2006 DNS of turbulent Couette flow with emphasis on the large-scale structure in the core region. J. Turbul. 7, N19.Google Scholar
Tuckerman, L. S. & Barkley, D. 2011 Patterns and dynamics in transitional plane Couette flow. Phys. Fluids 23 (4), 041301.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar