1 Introduction
Kelvin’s theorems occupy a central role in understanding the motion of ideal fluids as they help to establish basic connections between purely irrotational velocity potentials and rotational fields. Being relevant to both classical and quantum fluids, they continue to receive attention in various fundamental studies such as those pertaining to turbulence (Chen et al.
Reference Chen, Eyink, Wan and Xiao2006; Gregory Reference Gregory2006) and aerodynamic lift (Wu, Ma & Zhou Reference Wu, Ma and Zhou2006). Other interesting applications include a generalization of the minimum energy theorem to equivorticity flows (Arnold Reference Arnold1965) and the use of variational theory to specify the conditions for minimizing the kinetic energy of vortex motions (Chefranov & Chefranov Reference Chefranov and Chefranov2003). Of the many rich contributions attributed to Kelvin, the present work focuses on the minimum energy theorem. Devised in 1849, this theorem states that the irrotational motion
![]() $\bar{\boldsymbol{u}}$
of an incompressible fluid in a simply connected region contains less kinetic energy than any other motion
$\bar{\boldsymbol{u}}$
of an incompressible fluid in a simply connected region contains less kinetic energy than any other motion
![]() $\boldsymbol{u}$
with the same normal velocity at its boundary,
$\boldsymbol{u}$
with the same normal velocity at its boundary,
![]() $\bar{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}=\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}$
(Thomson Reference Thomson1849). The additional caveat is that, for a fluid extending to infinity, the theorem requires a vanishing normal velocity at the far-field boundary (Lamb Reference Lamb1895; Batchelor Reference Batchelor1967).
$\bar{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}=\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}$
(Thomson Reference Thomson1849). The additional caveat is that, for a fluid extending to infinity, the theorem requires a vanishing normal velocity at the far-field boundary (Lamb Reference Lamb1895; Batchelor Reference Batchelor1967).
Several direct consequences may be deduced from Kelvin’s theorem. First, it precludes the onset of irrotational motion in a simply connected, non-deformable region with rigid walls, where the potential velocity is nullified at all points on the boundary. Such a scenario is consistent with a system at rest or one with no kinetic energy. Second, for a non-deformable region with fixed rigid walls, no irrotational motion may be sustained when the velocity at infinity vanishes. Third, when the velocity at infinity is either null or uniform, a unique irrotational solution may be associated with a given motion of the internal boundary (Rouse Reference Rouse1959). In this work, we find that Kelvin’s minimum energy theorem continues to hold in regions where
![]() $\bar{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\neq \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}$
, provided that a simple criterion is met.
$\bar{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\neq \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}$
, provided that a simple criterion is met.
2 Basic analysis
In what follows, we assume that the rotational velocity fields are incompressible and regular.
Theorem 1 (For homogeneous and incompressible fluids with open boundaries).
The irrotational motion
![]() $\bar{\boldsymbol{u}}$
of a steady, homogeneous and incompressible fluid in a simply connected fluid region
$\bar{\boldsymbol{u}}$
of a steady, homogeneous and incompressible fluid in a simply connected fluid region
![]() ${\mathcal{V}}$
contains less kinetic energy than any another motion
${\mathcal{V}}$
contains less kinetic energy than any another motion
![]() $\boldsymbol{u}$
, with or without the same normal velocity at its boundary, provided that the following sufficient condition is met
$\boldsymbol{u}$
, with or without the same normal velocity at its boundary, provided that the following sufficient condition is met
where
![]() $\tilde{\boldsymbol{u}}=\boldsymbol{u}-\bar{\boldsymbol{u}}$
defines the net rotational component of the motion and
$\tilde{\boldsymbol{u}}=\boldsymbol{u}-\bar{\boldsymbol{u}}$
defines the net rotational component of the motion and
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $\boldsymbol{n}$
, and
$\boldsymbol{n}$
, and
![]() ${\mathcal{S}}$
denote the velocity potential, normal unit vector and boundary surface, respectively.
${\mathcal{S}}$
denote the velocity potential, normal unit vector and boundary surface, respectively.

Figure 1. Volume of fluid showing surfaces with different net rotational velocities at the boundaries.
Proof. With
![]() $\bar{\boldsymbol{u}}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
being a steady, single-valued velocity component of a homogeneously incompressible fluid occupying a simply connected volume of fluid
$\bar{\boldsymbol{u}}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
being a steady, single-valued velocity component of a homogeneously incompressible fluid occupying a simply connected volume of fluid
![]() ${\mathcal{V}}$
, then
${\mathcal{V}}$
, then
![]() $\tilde{\boldsymbol{u}}=\boldsymbol{u}-\bar{\boldsymbol{u}}$
refers to the (net) rotational contribution and difference between the velocity of another (rotational) motion satisfying continuity and the potential solution
$\tilde{\boldsymbol{u}}=\boldsymbol{u}-\bar{\boldsymbol{u}}$
refers to the (net) rotational contribution and difference between the velocity of another (rotational) motion satisfying continuity and the potential solution
![]() $\bar{\boldsymbol{u}}$
(see figure 1). These fields are incompressible and so, by virtue of mass conservation, one may put
$\bar{\boldsymbol{u}}$
(see figure 1). These fields are incompressible and so, by virtue of mass conservation, one may put
Pursuant to Kelvin’s argument,
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\bar{\boldsymbol{u}}$
must exhibit the same normal velocity along the boundary of
$\bar{\boldsymbol{u}}$
must exhibit the same normal velocity along the boundary of
![]() ${\mathcal{V}}$
or else vanish. For steady, homogeneous, incompressible motion, we choose
${\mathcal{V}}$
or else vanish. For steady, homogeneous, incompressible motion, we choose
![]() $T$
and
$T$
and
![]() $\bar{T}$
to represent the specific kinetic energies associated with
$\bar{T}$
to represent the specific kinetic energies associated with
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\bar{\boldsymbol{u}}$
, respectively. Subsequently, the energy contribution due to rotationality may be calculated from
$\bar{\boldsymbol{u}}$
, respectively. Subsequently, the energy contribution due to rotationality may be calculated from
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T & = & \displaystyle T-\bar{T}=\frac{1}{2}\iiint _{{\mathcal{V}}}(\boldsymbol{u}^{2}-\bar{\boldsymbol{u}}^{2})\,\text{d}{\mathcal{V}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\iiint _{{\mathcal{V}}}[(\boldsymbol{u}-\bar{\boldsymbol{u}})^{2}+2(\boldsymbol{u}-\bar{\boldsymbol{u}})\boldsymbol{\cdot }\bar{\boldsymbol{u}}]\,\text{d}{\mathcal{V}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\iiint _{{\mathcal{V}}}\tilde{\boldsymbol{u}}^{2}\,\text{d}{\mathcal{V}}+\iiint _{{\mathcal{V}}}\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\,\text{d}{\mathcal{V}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}T & = & \displaystyle T-\bar{T}=\frac{1}{2}\iiint _{{\mathcal{V}}}(\boldsymbol{u}^{2}-\bar{\boldsymbol{u}}^{2})\,\text{d}{\mathcal{V}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\iiint _{{\mathcal{V}}}[(\boldsymbol{u}-\bar{\boldsymbol{u}})^{2}+2(\boldsymbol{u}-\bar{\boldsymbol{u}})\boldsymbol{\cdot }\bar{\boldsymbol{u}}]\,\text{d}{\mathcal{V}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\iiint _{{\mathcal{V}}}\tilde{\boldsymbol{u}}^{2}\,\text{d}{\mathcal{V}}+\iiint _{{\mathcal{V}}}\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\,\text{d}{\mathcal{V}}.\end{eqnarray}$$
The last member of (2.3) may be simplified through the use of
![]() $\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D719}\,\tilde{\boldsymbol{u}})-\unicode[STIX]{x1D719}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D719}\tilde{\boldsymbol{u}})$
in conjunction with the divergence theorem. One is left with
$\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D719}\,\tilde{\boldsymbol{u}})-\unicode[STIX]{x1D719}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D719}\tilde{\boldsymbol{u}})$
in conjunction with the divergence theorem. One is left with
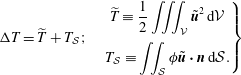 $$\begin{eqnarray}\unicode[STIX]{x0394}T=\widetilde{T}+T_{{\mathcal{S}}};\quad \left.\begin{array}{@{}c@{}}\displaystyle \widetilde{T}\equiv \frac{1}{2}\iiint _{{\mathcal{V}}}\tilde{\boldsymbol{u}}^{2}\,\text{d}{\mathcal{V}}\\ \displaystyle T_{{\mathcal{S}}}\equiv \iint _{{\mathcal{S}}}\unicode[STIX]{x1D719}\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}{\mathcal{S}}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0394}T=\widetilde{T}+T_{{\mathcal{S}}};\quad \left.\begin{array}{@{}c@{}}\displaystyle \widetilde{T}\equiv \frac{1}{2}\iiint _{{\mathcal{V}}}\tilde{\boldsymbol{u}}^{2}\,\text{d}{\mathcal{V}}\\ \displaystyle T_{{\mathcal{S}}}\equiv \iint _{{\mathcal{S}}}\unicode[STIX]{x1D719}\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}{\mathcal{S}}.\end{array}\right\}\end{eqnarray}$$
In constructing Kelvin’s theorem, the net rotational motion vanishes on all boundaries, thus yielding
![]() $\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}=0$
on
$\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}=0$
on
![]() ${\mathcal{S}}$
. This permits setting
${\mathcal{S}}$
. This permits setting
![]() $T_{{\mathcal{S}}}=0$
in (2.4) and deducing that
$T_{{\mathcal{S}}}=0$
in (2.4) and deducing that
![]() $\unicode[STIX]{x0394}T\geqslant 0$
given that
$\unicode[STIX]{x0394}T\geqslant 0$
given that
![]() $\widetilde{T}\geqslant 0$
for any rotational field. It can therefore be seen that
$\widetilde{T}\geqslant 0$
for any rotational field. It can therefore be seen that
![]() $\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}=0$
ensures that the energy associated with the potential motion remains a minimum. However, in the general case of
$\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}=0$
ensures that the energy associated with the potential motion remains a minimum. However, in the general case of
![]() $\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\neq 0$
, it is possible for
$\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\neq 0$
, it is possible for
![]() $T_{{\mathcal{S}}}\neq 0$
. Clearly, in order for
$T_{{\mathcal{S}}}\neq 0$
. Clearly, in order for
![]() $\unicode[STIX]{x0394}T\geqslant 0$
, it is necessary and sufficient to impose
$\unicode[STIX]{x0394}T\geqslant 0$
, it is necessary and sufficient to impose
Recognizing that the first term in (2.5) is always positive, it is sufficient to show that
Kelvin’s theorem may thus be extended to the flow of homogeneously incompressible fluids in regions with open boundaries when either of the two above conditions is fulfilled. ☐
3 Discussion
According to Batchelor (Reference Batchelor1967), Kelvin’s theorem ceases to hold for a multi-valued potential, such as the one corresponding to the flow in multiply connected regions, unless one selects the particular irrotational motion that bears the least kinetic energy among all potential solutions. Alternatively, if one defines a velocity potential as the difference between two possible potential solutions having the same cyclic constant (
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{0}-\unicode[STIX]{x1D719}_{1}$
), then the theorem can be applied because of the uniqueness of the resulting potential.
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{0}-\unicode[STIX]{x1D719}_{1}$
), then the theorem can be applied because of the uniqueness of the resulting potential.
Since velocity potentials may be specified up to an additive constant
![]() $K$
, the effect of
$K$
, the effect of
![]() $K$
on (2.6) must be examined. In this case, we replace
$K$
on (2.6) must be examined. In this case, we replace
![]() $\unicode[STIX]{x1D719}$
by
$\unicode[STIX]{x1D719}$
by
![]() $(\unicode[STIX]{x1D719}+K)$
in (2.6) and recover
$(\unicode[STIX]{x1D719}+K)$
in (2.6) and recover
where the divergence-free property of the net rotational motion is used to reduce the above integral (
![]() $\iint _{{\mathcal{S}}}\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}{\mathcal{S}}=0$
). It can thus be seen that, for single-valued velocity potentials, the extended Kelvin criterion is not affected by the addition of an arbitrary constant to the potential.
$\iint _{{\mathcal{S}}}\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}{\mathcal{S}}=0$
). It can thus be seen that, for single-valued velocity potentials, the extended Kelvin criterion is not affected by the addition of an arbitrary constant to the potential.
From a practical standpoint, it may be useful to check whether the evaluation of the surface integral in (2.6) will be more straightforward than the volume integral
![]() $\iiint _{{\mathcal{V}}}(\boldsymbol{u}^{2}-\bar{\boldsymbol{u}}^{2})\,\text{d}{\mathcal{V}}$
. Such a verification will require an assessment of the algebraic complexity of the integrals in question as well as the cost of computing them individually.
$\iiint _{{\mathcal{V}}}(\boldsymbol{u}^{2}-\bar{\boldsymbol{u}}^{2})\,\text{d}{\mathcal{V}}$
. Such a verification will require an assessment of the algebraic complexity of the integrals in question as well as the cost of computing them individually.
In terms of algebraic complexity, it can be argued that the presence of squares in the volume integral can lead to nonlinear expressions and, hence, more tedious algebraic manipulations. In contrast, it is likely for the surface integral to require less effort to evaluate.
Another benefit of evaluating (2.6) versus (2.3) is associated with the cost of numerical computation. To illustrate this point, we define the speed-up factor as the ratio of the time needed to compute the volume integral to that needed to compute its corresponding surface integral,
![]() $t_{{\mathcal{V}}}/t_{{\mathcal{S}}}$
. We then calculate the speed up for three representative problems that are well known in the community. These are (i) the Poiseuille motion in a duct, (ii) the Taylor motion in a porous channel (Taylor Reference Taylor1956) and (iii) the Taylor–Culick motion in a porous cylinder (Culick Reference Culick1966). The corresponding computations are carried out using quadrature routines provided by the NumPy library in Python within machine precision. For the reader’s convenience, speed-up results are catalogued in table 1, where the speed of computing volume integrals is seen to range from approximately 20 to 30 times the speed of computing the corresponding surface integrals.
$t_{{\mathcal{V}}}/t_{{\mathcal{S}}}$
. We then calculate the speed up for three representative problems that are well known in the community. These are (i) the Poiseuille motion in a duct, (ii) the Taylor motion in a porous channel (Taylor Reference Taylor1956) and (iii) the Taylor–Culick motion in a porous cylinder (Culick Reference Culick1966). The corresponding computations are carried out using quadrature routines provided by the NumPy library in Python within machine precision. For the reader’s convenience, speed-up results are catalogued in table 1, where the speed of computing volume integrals is seen to range from approximately 20 to 30 times the speed of computing the corresponding surface integrals.
Table 1. Speed advantage of numerically computing the surface integral (2.6) relative to the volume integral (2.3) for the cases of: (i) Poiseuille flow in a duct, (ii) Taylor flow in a porous channel and (iii) Taylor–Culick flow in a porous cylinder. The speed-up factor is defined as the ratio of the time needed to compute the volume integral to that needed to compute the surface integral. Depending on the coordinate system used,
![]() $\boldsymbol{e}_{x}$
,
$\boldsymbol{e}_{x}$
,
![]() $\boldsymbol{e}_{y}$
,
$\boldsymbol{e}_{y}$
,
![]() $\boldsymbol{e}_{r}$
and
$\boldsymbol{e}_{r}$
and
![]() $\boldsymbol{e}_{z}$
refer to the unit vectors in the
$\boldsymbol{e}_{z}$
refer to the unit vectors in the
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $r$
and
$r$
and
![]() $z$
directions, respectively.
$z$
directions, respectively.

It should be noted that, when the normal velocities on the boundary for a given potential motion and for other flows are allowed to differ, our simple condition ensures that the given potential motion will still possess the least energy. It is hoped that other researchers will be interested in generating additional verifications and proofs or, perhaps, exceptions and exclusions that we may have overlooked.
4 Conclusion
The present analysis seeks to address the viability of Kelvin’s incompressible theorem in regions where the normal velocity components of the irrotational and rotational motions are allowed to differ. Our work suggests that Kelvin’s minimum energy statement is connected to the sign of an integral that strictly depends on the rotational flux over the boundary as well as the local velocity potential. This no longer requires a vanishing or uniform velocity field at infinity for the theorem to stand. Instead, the ability of the present analysis to account for irregular velocity distributions at fluid boundaries grants Kelvin’s theorem broader applicability to fluid regions with arbitrary velocity distributions in homogeneous and incompressible flow fields.
Acknowledgements
This material is based on work supported partly by the National Science Foundation, and partly by Auburn University, Department of Aerospace Engineering, through the Hugh and Loeda Francis Chair of Excellence. The authors thank Professor J.-Z. Wu of Peking University for his insightful comments regarding the limitations of Lord Kelvin’s classic energy theorem.





