Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T11:43:05.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Experiments on a jet in a crossflow in the low-velocity-ratio regime

Published online by Cambridge University Press:  29 January 2019

L. Klotz Open the ORCID record for L. Klotz [Opens in a new window] ,
K. Gumowski Open the ORCID record for K. Gumowski [Opens in a new window]  and
J. E. Wesfreid Open the ORCID record for J. E. Wesfreid [Opens in a new window]
L. Klotz*
Affiliation:
Institute of Science and Technology, Am Campus 1, 3400 Klosterneuburg, Austria Institute of Aeronautics and Applied Mechanics, Warsaw University of Technology, Nowowiejska 24, 00-665 Warsaw, Poland
K. Gumowski
Affiliation:
Institute of Aeronautics and Applied Mechanics, Warsaw University of Technology, Nowowiejska 24, 00-665 Warsaw, Poland
J. E. Wesfreid
Affiliation:
Physique et Mécanique des Milieux Hétérogènes, ESPCI Paris, PSL University, CNRS, Sorbonne Université, Université Paris Diderot, Sorbonne Paris Cité, 75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

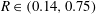The hairpin instability of a jet in a crossflow (JICF) for a low jet-to-crossflow velocity ratio is investigated experimentally for a velocity ratio range of $R\in (0.14,0.75)$ and crossflow Reynolds numbers 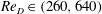$Re_{D}\in (260,640)$. From spectral analysis we characterize the Strouhal number and amplitude of the hairpin instability as a function of 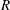$R$ and 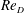$Re_{D}$. We demonstrate that the dynamics of the hairpins is well described by the Landau model, and, hence, that the instability occurs through Hopf bifurcation, similarly to other hydrodynamical oscillators such as wake behind different bluff bodies. Using the Landau model, we determine the precise threshold values of hairpin shedding. We also study the spatial dependence of this hydrodynamical instability, which shows a global behaviour.

JFM classification

Wakes/Jets: Jets Instability: Nonlinear instability Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 386 - 406
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acarlar, M. S. & Smith, C. R. 1987a A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance. J. Fluid Mech. 175, 1–41.10.1017/S0022112087000272Google Scholar
Acarlar, M. S. & Smith, C. R. 1987b A study of hairpin vortices in a laminar boundary layer. Part 2. Hairpin vortices generated by fluid injection. J. Fluid Mech. 175, 43–83.10.1017/S0022112087000284Google Scholar
Bidan, G. & Nikitopoulos, D. E. 2013 On steady and pulsed low-blowing-ratio transverse jets. J. Fluid Mech. 714, 393–433.10.1017/jfm.2012.482Google Scholar
Bobinski, T., Goujon-Durand, S. & Wesfreid, J. E. 2014 Instabilities in the wake of a circular disk. Phys. Rev. E 89 (5), 053021.Google Scholar
Bucci, M. A., Puckert, D. K., Andriano, C., Loiseau, J.-Ch., Cherubini, S., Robinet, J.-Ch. & Rist, U. 2018 Roughness-induced transition by quasi-resonance of a varicose global mode. J. Fluid Mech. 836, 167–191.10.1017/jfm.2017.791Google Scholar
Cambonie, T. & Aider, J.-L. 2014 Transition scenario of the round jet in crossflow topology at low velocity ratios. Phys. Fluids 26 (8), 084101.10.1063/1.4891850Google Scholar
Camussi, R., Guj, G. & Stella, A. 2002 Experimental study of a jet in a crossflow at very low Reynolds number. J. Fluid Mech. 454, 113–144.10.1017/S0022112001007005Google Scholar
Chauvat, G., Peplinski, A., Hanifi, A. & Henningson, D. S. 2017 Global Stability of a Jet in Cross-Flow: Effects of Jet Inflow. Stockholm, Sweden: 16th European Turbulence Conference.Google Scholar
Davitian, J., Getsinger, D., Hendrickson, C. & Karagozian, A. R. 2010 Transition to global instability in transverse-jet shear layers. J. Fluid Mech. 661, 294–315.10.1017/S0022112010003046Google Scholar
Getsinger, D. R., Gevorkyan, L., Smith, O. I. & Karagozian, A. R. 2014 Structural and stability characteristics of jets in crossflow. J. Fluid Mech. 760, 342–367.10.1017/jfm.2014.605Google Scholar
Gevorkyan, L., Shoji, T., Peng, W. Y. & Karagozian, A. R. 2018 Influence of the velocity field on scalar transport in gaseous transverse jets. J. Fluid Mech. 834, 173–219.10.1017/jfm.2017.621Google Scholar
Gopalan, S., Abraham, B. M. & Katz, J. 2004 The structure of a jet in cross flow at low velocity ratios. Phys. Fluids 16 (6), 2067–2087.10.1063/1.1697397Google Scholar
Goujon-Durand, S., Jenffer, P. & Wesfreid, J. E. 1994 Downstream evolution of the Bénard-von Kármán instability. Phys. Rev. E 50 (1), 308–313.Google Scholar
Gumowski, K., Miedzik, J., Goujon-Durand, S., Jenffer, P. & Wesfreid, J. E. 2008 Transition to a time-dependent state of fluid flow in the wake of a sphere. Phys. Rev. E 77 (5), 055308.Google Scholar
Ilak, M., Schlatter, P., Bagheri, S. & Henningson, D. S. 2012 Bifurcation and stability analysis of a jet in cross-flow: onset of global instability at a low velocity ratio. J. Fluid Mech. 696, 94–121.10.1017/jfm.2012.10Google Scholar
Iyer, P. S. & Mahesh, K. 2016 A numerical study of shear layer characteristics of low-speed transverse jets. J. Fluid Mech. 790, 275–307.10.1017/jfm.2016.7Google Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.10.1017/S0022112098003206Google Scholar
Jovanović, M. B., de Lange, H. C. & van Steenhoven, A. A. 2008 Effect of hole imperfection on adiabatic film cooling effectiveness. Intl J. Heat Fluid Flow 29 (2), 377–386.10.1016/j.ijheatfluidflow.2007.11.008Google Scholar
Karagozian, A. R. 2010 Transverse jets and their control. Prog. Energy Combust. Sci. 36 (5), 531–553.10.1016/j.pecs.2010.01.001Google Scholar
Karagozian, A. R. 2014 The jet in crossflow. Phys. Fluids 26 (10), 101303.10.1063/1.4895900Google Scholar
Kelso, R. M. & Smits, A. J. 1995 Horseshoe vortex systems resulting from the interaction between a laminar boundary layer and a transverse jet. Phys. Fluids 7 (1), 153–158.10.1063/1.868736Google Scholar
Klotz, L., Goujon-Durand, S., Rokicki, J. & Wesfreid, J. E. 2014 Experimental investigation of flow behind a cube for moderate Reynolds numbers. J. Fluid Mech. 750, 73–98.10.1017/jfm.2014.236Google Scholar
Klotz, L. & Wesfreid, J. E. 2017 Experiments on transient growth of turbulent spots. J. Fluid Mech. 829, R4.10.1017/jfm.2017.614Google Scholar
Lim, T. T., New, T. H. & Luo, S. C. 2001 On the development of large-scale structures of a jet normal to a cross flow. Phys. Fluids 13 (3), 770–775.10.1063/1.1347960Google Scholar
Mahesh, K. 2013 The interaction of jets with crossflow. Annu. Rev. Fluid Mech. 45 (1), 379–407.10.1146/annurev-fluid-120710-101115Google Scholar
Margason, R. J.1993 Fifty years of jet in cross flow research. AGARD-CP 534, Comp. and Exp. Assess. Jets in Cross Flow.Google Scholar
Mathis, C., Provansal, M. & Boyer, L. 1984 The Benard-Von Karman instability: an experimental study near the threshold. J. Phys. Lett. 45 (10), 483–491.10.1051/jphyslet:019840045010048300Google Scholar
Megerian, S., Davitian, J., Alves, L. S. De B. & Karagozian, A. R. 2007 Transverse-jet shear-layer instabilities. Part 1. Experimental studies. J. Fluid Mech. 593, 93–129.10.1017/S0022112007008385Google Scholar
Ormires, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83 (1), 80–83.10.1103/PhysRevLett.83.80Google Scholar
Peplinski, A., Schlatter, P. & Henningson, D. S. 2015a Global stability and optimal perturbation for a jet in cross-flow. Eur. J. Mech. (B/Fluids) 49 (Part B), 438–447.10.1016/j.euromechflu.2014.06.001Google Scholar
Peplinski, A., Schlatter, P. & Henningson, D. S. 2015b Investigations of stability and transition of a jet in crossflow using DNS. In Instability and Control of Massively Separated Flows, Fluid Mechanics and Its Applications, vol. 107, pp. 7–18. Springer.Google Scholar
Regan, M. A. & Mahesh, K. 2017 Global linear stability analysis of jets in cross-flow. J. Fluid Mech. 828, 812–836.10.1017/jfm.2017.489Google Scholar
Sau, R. & Mahesh, K. 2008 Dynamics and mixing of vortex rings in crossflow. J. Fluid Mech. 604, 389–409.10.1017/S0022112008001328Google Scholar
Schlatter, P., Bagheri, S. & Henningson, D. S. 2011 Self-sustained global oscillations in a jet in crossflow. Theor. Comput. Fluid Dyn. 25 (1–4), 129–146.10.1007/s00162-010-0199-1Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.10.1007/978-1-4613-0185-1Google Scholar
Wesfreid, J. E., Goujon-Durand, S. & Zielinska, B. J. A. 1996 Global mode behavior of the streamwise velocity in wakes. J. Phys. (Paris) II 6 (10), 1343–1357.Google Scholar
Zielinska, B. J. A. & Wesfreid, J. E. 1995 On the spatial structure of global modes in wake flow. Phys. Fluids 7 (6), 1418–1424.10.1063/1.868529Google Scholar