No CrossRef data available.
Published online by Cambridge University Press: 25 November 2024
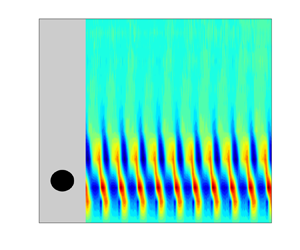
Investigations are conducted on the effect of wall proximity on the flow around a cylinder under an axial magnetic field, using the electrical potential probe technology to measure the velocity of liquid metal flow. The study focused on the impact of the inlet velocity of the fluid, the magnetic field and wall proximity on the characteristics of velocity fields, particularly on the vortex-shedding mode. Based on different magnitudes of the magnetic field and the distance from the cylinder to the duct wall, three types of vortex-shedding modes are identified, (I) shear layer oscillation state, (II) quasi-two-dimensional vortex-shedding states and (III) transition of the magnetohydrodynamic to hydrodynamic Kármán street. The transitions between these modes are analysed in detail. The experimental results show that the weak wall-proximity effect leads to the formation of the Kármán vortex street, while a reverse Kármán vortex street and secondary vortices emerge under a strong wall-proximity effect. It is noticed that the Kelvin–Helmholtz instability drives vortex shedding under regime I, leading to an increase in the Strouhal number (St) with stronger magnetic fields. Additionally, under a strong axial magnetic field, the wall-proximity effect (‘Shercliff layer effect’) promotes the instability of shear layers on both sides of the cylinder. These unique coupling effects are validated by variations in modal coefficients and energy proportions under different vortex-shedding regimes using the proper orthogonal decomposition method.