Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T13:45:16.112Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study on dominant vortex structures in near-wall region of turbulent boundary layer based on tomographic particle image velocimetry

Published online by Cambridge University Press:  09 July 2019

Chengyue Wang ,
Qi Gao Open the ORCID record for Qi Gao [Opens in a new window] ,
Jinjun Wang Open the ORCID record for Jinjun Wang [Opens in a new window] ,
Biao Wang  and
Chong Pan Open the ORCID record for Chong Pan [Opens in a new window]
Chengyue Wang
Affiliation:
Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519000, China
Qi Gao*
Affiliation:
School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China
Jinjun Wang
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beihang University, Beijing 100191, China
Biao Wang
Affiliation:
Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519000, China
Chong Pan
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beihang University, Beijing 100191, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

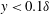Vortex structures are very popular research objects in turbulent boundary layers (TBLs) because of their prime importance in turbulence modelling. This work performs a tomographic particle image velocimetry measurement on the near-wall region ($y<0.1\unicode[STIX]{x1D6FF}$) of TBLs at three Reynolds numbers $Re_{\unicode[STIX]{x1D70F}}=1238$, 2286 and 3081. The main attention is paid to the wall-normal evolution of the vortex geometries and topologies. The vortex is identified with swirl strength (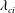$\unicode[STIX]{x1D706}_{ci}$), and its orientation is recognized by using the real eigenvector of the velocity gradient tensor. The vortex inclination angles in the streamwise–wall-normal plane and in the streamwise–spanwise plane as functions of wall-normal positions are investigated, which provide useful information to speculate on the three-dimensional shape of the vortex tubes in a TBL. The difference between the orientations of vorticity and swirl is discussed and their inherent relationship is revealed based on the governing equation of vorticity. Linear stochastic estimation (LSE) is further deployed to directly extract three-dimensional vortex models. The LSE velocity fields for ejection events happening at different wall-normal positions shed light on the evolution of the topologies for the vortices dominating ejection events. LSE based on a centred prograde spanwise vortex provides a typical packet model, which indicates that the population density of the packets in a TBL is large enough to leave footprints in conditionally averaged flow fields. This work should help to settle the severe debate on the existence of packet structures and also lays some foundation for the TBL model theory.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 426 - 454
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1979 Conditional eddies in isotropic turbulence. Phys. Fluids 22 (11), 2065–2070.10.1063/1.862515Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.10.1063/1.2717527Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.10.1017/S0022112000001580Google Scholar
Berlant, L. 2008 Streak interactions and breakdown in boundary layer flows. Phys. Fluids 20 (2), 243–422.Google Scholar
Bernard, P. S., Thomas, J. M. & Handler, R. A. 1993 Vortex dynamics and the production of Reynolds stress. J. Fluid Mech. 253, 385–419.10.1017/S0022112093001843Google Scholar
Borrell, G., Sillero, J. A. & Jiménez, J. 2013 A code for direct numerical simulation of turbulent boundary layers at high Reynolds numbers in BG/P supercomputers. Comput. Fluids 80 (1), 37–43.10.1016/j.compfluid.2012.07.004Google Scholar
Chauhan, K. A., Nagib, H. M. & Monkewitz, P. A. 2007 On the composite logarithmic profile in zero pressure gradient turbulent boundary layers. In 45th AIAA Aerospace Sciences Meeting and Exhibit (AIAA). Reno, NV. AIAA.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.10.1017/S0022112001003512Google Scholar
Das, S. K., Tanahashi, M., Shoji, K. & Miyauchi, T. 2006 Statistical properties of coherent fine eddies in wall-bounded turbulent flows by direct numerical simulation. Theor. Comput. Fluid Dyn. 20 (2), 55–71.10.1007/s00162-006-0008-zGoogle Scholar
Del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.10.1017/S0022112006000814Google Scholar
Deng, S., Pan, C., Wang, J. & He, G. 2018 On the spatial organization of hairpin packets in a turbulent boundary layer at low-to-moderate Reynolds number. J. Fluid Mech. 844, 635–668.10.1017/jfm.2018.160Google Scholar
Elsinga, G. E., Adrian, R. J., Oudheusden, B. W. V. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.10.1017/S0022112009992047Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.10.1017/S0022112002003270Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2006 Experimental investigation of vortex properties in a turbulent boundary layer. Phys. Fluids 18 (5), 1–464.Google Scholar
Gao, Q., Ortiz-Duenas, C. & Longmire, E. K. 2007 Circulation signature of vortical structures in turbulent boundary layers. In 16th Australasian Fluid Mechanics Conference (AFMC), Gold Coast, Queensland, Australia. The University of Queensland.Google Scholar
Gao, Q., Ortizdueñas, C. & Longmire, E. K. 2011 Analysis of vortex populations in turbulent wall-bounded flows. J. Fluid Mech. 678, 87–123.10.1017/jfm.2011.101Google Scholar
Goudar, M. V., Breugem, W. P. & Elsinga, G. E. 2016 Auto-generation in wall turbulence by the interaction of weak eddies. Phys. Fluids 28 (3), 035111.10.1063/1.4944048Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.10.1017/S0022112081001791Google Scholar
Herpin, S., Stanislas, M., Jean, M. F. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.10.1017/jfm.2012.491Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.10.1017/S0022112009007721Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structure near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.10.1017/S0022112096003965Google Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.10.1017/jfm.2018.144Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.10.1017/S0022112099005066Google Scholar
Jodai, Y. & Elsinga, G. E. 2016 Experimental observation of hairpin auto-generation events in a turbulent boundary layer. J. Fluid Mech. 795, 611–633.10.1017/jfm.2016.153Google Scholar
Kang, S., Tanahashi, M. & Miyauchi, T. 2007 Dynamics of fine scale eddy clusters in turbulent channel flows. J. Turbul. 8, 1–19.Google Scholar
Kendall, A. & Koochesfahani, M. 2008 A method for estimating wall friction in turbulent wall-bounded flows. Exp. Fluids 44 (5), 773–780.10.1007/s00348-007-0433-9Google Scholar
Liu, C., Gao, Y., Tian, S. & Dong, X. 2018 Rortex – a new vortex vector definition and vorticity tensor and vector decompositions. Phys. Fluids 30 (3), 035103.10.1063/1.5023001Google Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (13), 735–743.10.1063/1.1343480Google Scholar
Marusic, I. & Monty, J. P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51 (1), 49–74.10.1146/annurev-fluid-010518-040427Google Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.10.1017/S0022112095003363Google Scholar
Moin, P. & Kim, J. 1984 The structure of the vorticity field in turbulent channel flow. Part 1. Analysis of instantaneous fields and statistical correlations. J. Fluid Mech. 155, 441–464.10.1017/S0022112085001896Google Scholar
Ong, L. & Wallace, J. M. 1998 Joint probability density analysis of the structure and dynamics of the vorticity field of a turbulent boundary layer. J. Fluid Mech. 367, 291–328.10.1017/S002211209800158XGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.10.1017/S0022112095003351Google Scholar
Pirozzoli, S., Bernardini, M. & Grasso, F. 2008 Characterization of coherent vortical structures in a supersonic turbulent boundary layer. J. Fluid Mech. 613, 205–231.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.10.1146/annurev.fl.23.010191.003125Google Scholar
Schlatter, P., Orlu, R., Li, Q., Hussain, F. & Henningson, D. 2014 On the near-wall vortical structures at high Reynolds numbers. Eur. J. Mech. (B/Fluids) 48 (6), 75–93.10.1016/j.euromechflu.2014.04.011Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.10.1017/S002211200100667XGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛥+ ≈ 2000. Phys. Fluids 25 (10), 133–166.10.1063/1.4823831Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛥+ ≈ 2000. Phys. Fluids 26 (10), 1–15.10.1063/1.4899259Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2015 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.10.1017/jfm.2015.672Google Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228 (11), 4218–4231.10.1016/j.jcp.2009.02.031Google Scholar
Stanislas, M., Perret, L. & Foucaut, J. M. 2008 Vortical structures in the turbulent boundary layer: a possible route to a universal representation. J. Fluid Mech. 602, 327–382.10.1017/S0022112008000803Google Scholar
Tanahashi, M., Kang, S. J., Miyamoto, T., Shiokawa, S. & Miyauchi, T. 2004 Scaling law of fine scale eddies in turbulent channel flows up to Re 𝜏 = 800. Intl J. Heat Fluid Flow 25 (3), 331–340.10.1016/j.ijheatfluidflow.2004.02.016Google Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In The Midwestern Conference on Fluid Mechanics, Ohio State University, Columbus, OH.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Wallace, J. M., Brodkey, R. S. & Eckelmann, H. 1977 Pattern-recognized structures in bounded turbulent shear flows. J. Fluid Mech. 83 (4), 673–693.10.1017/S0022112077001402Google Scholar
Wang, C., Gao, Q., Wang, H., Wei, R., Li, T. & Wang, J. 2016a Divergence-free smoothing for volumetric PIV data. Exp. Fluids 57 (1), 1–23.Google Scholar
Wang, H. P., Gao, Q., Wei, R. J. & Wang, J. J. 2016b Intensity-enhanced MART for tomographic PIV. Exp. Fluids 57 (5), 87.10.1007/s00348-016-2176-yGoogle Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 97–120.10.1063/1.4905301Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.10.1017/S0022112009006624Google Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.10.1017/S002211200600259XGoogle Scholar
Ye, Z. J., Gao, Q., Wang, H. P., Wei, R. J. & Wang, J. J. 2015 Dual-basis reconstruction techniques for tomographic PIV. Sci. Chin. 58 (11), 1963–1970.10.1007/s11431-015-5909-xGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.10.1017/S002211209900467XGoogle Scholar