Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-09T22:04:45.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of the turbulent boundary layer in acceleration-skewed oscillatory flow

Published online by Cambridge University Press:  06 September 2011

Dominic A. van der A ,
Tom O’Donoghue ,
Alan G. Davies  and
Jan S. Ribberink
Dominic A. van der A*
Affiliation:
School of Engineering, University of Aberdeen, Aberdeen AB24 3UE, UK
Tom O’Donoghue
Affiliation:
School of Engineering, University of Aberdeen, Aberdeen AB24 3UE, UK
Alan G. Davies
Affiliation:
School of Ocean Sciences, Bangor University, Menai Bridge, Anglesey LL59 5AB, UK
Jan S. Ribberink
Affiliation:
Department of Water Engineering and Management, University of Twente, Enschede, PO Box 217, 7500 AE, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Experiments have been conducted in a large oscillatory flow tunnel to investigate the effects of acceleration skewness on oscillatory boundary layer flow over fixed beds. As well as enabling experimental investigation of the effects of acceleration skewness, the new experiments add substantially to the relatively few existing detailed experimental datasets for oscillatory boundary layer flow conditions that correspond to full-scale sea wave conditions. 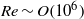Two types of bed roughness and a range of high-Reynolds-number, , oscillatory flow conditions, varying from sinusoidal to highly acceleration-skewed, are considered. Results show the structure of the intra-wave velocity profile, the time-averaged residual flow and boundary layer thickness for varying degrees of acceleration skewness, 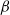. Turbulence intensity measurements from particle image velocimetry (PIV) and laser Doppler anemometry (LDA) show very good agreement. Turbulence intensity and Reynolds stress increase as the flow accelerates after flow reversal, are maximum at around maximum free-stream velocity and decay as the flow decelerates. The intra-wave turbulence depends strongly on 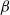but period-averaged turbulent quantities are largely independent of 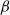. There is generally good agreement between bed shear stress estimates obtained using the log-law and using the momentum integral equation, and flow acceleration skewness leads to high bed shear stress asymmetry between flow half-cycles. Turbulent Reynolds stress is much less than the shear stress obtained from the momentum integral; analysis of the stress contributors shows that significant phase-averaged vertical velocities exist near the bed throughout the flow cycle, which lead to an additional shear stress, 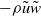; near the bed this stress is at least as large as the turbulent Reynolds stress.

JFM classification

Geophysical and Geological Flows: Coastal engineering Geophysical and Geological Flows: Geophysical and Geological Flows Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 251 - 283
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. van der A, D. A., O’Donoghue, T. & Ribberink, J. S. 2010 Measurements of sheet flow transport in acceleration-skewed oscillatory flow and comparison with practical formulations. Coast. Engng 57, 331–342.Google Scholar
2. Bucchave, P., George, W. K. & Lumley, J. L. 1979 The measurement of turbulence with the laser-doppler anemometer. Annu. Rev. Fluid Mech. 11, 443–503.CrossRefGoogle Scholar
3. Chen, D., Chen, C., Tang, F.-E., Stansby, P. & Li, M. 2007 Boundary layer structure of oscillatory open-channel shallow flows over smooth and rough beds. Exp. Fluids 42, 719–736.CrossRefGoogle Scholar
4. Coleman, S. E., Nikora, V. I. & Schlicke, T. 2008 Spatially-averaged oscillatory flow over a rough bed. Acta Geophys. 56, 698–733.CrossRefGoogle Scholar
5. Conley, D. C. & Inman, D. L. 1994 Ventilated oscillatory boundary layers. J. Fluid Mech. 273, 261–284.CrossRefGoogle Scholar
6. Cox, D. T., Kobayashi, N. & Okayasu, A. 1996 Bottom shear stress in the surf zone. J. Geophys. Res. 101 (C6), 14337–14348.Google Scholar
7. Davies, A. G. & Li, Z. 1997 Modelling sediment transport beneath regular symmetrical and asymmetrical waves above a plane bed. Cont. Shelf Res. 17, 555–582.CrossRefGoogle Scholar
8. Davies, A. G. & Villaret, C. 1997 Oscillatory flow over rippled bed: boundary layer structure and wave-induced Eulerian drift. In Gravity Waves in Water of Finite Depth, Advances in Fluid Mechanics (ed. Hunt, J. ), pp. 215–254. Computational Mechanics Publications.Google Scholar
9. Dixen, M., Hatipoglu, F., Sumer, B. M. & Fredsøe, E. J. 2008 Wave boundary layer over a stone-covered bed. Coast. Engng 55, 1–20.CrossRefGoogle Scholar
10. Dohmen-Janssen, C. M., Kroekenstoel, D. F., Hassan, W. N. & Ribberink, J. S. 2002 Phase lags in oscillatory sheet flow: experiments and bed load modelling. Coast. Engng 46, 61–87.CrossRefGoogle Scholar
11. Elfrink, B., Hanes, D. M. & Ruessink, B. G. 2006 Parameterization and simulation of near bed orbital velocities under irregular waves in shallow water. Coast. Engng 53, 915–927.Google Scholar
12. Elgar, S., Gallagher, E. L. & Guza, R. T. 2001 Nearshore sandbar migration. J. Geophys. Res. 106 (C6), 11623–11627.Google Scholar
13. Foster, D. L., Guenther, R. A. & Holman, R. A. 1999 An analytic solution to the wave bottom boundary layer governing equation under arbitrary wave forcing. Ocean Engng 26, 595–623.CrossRefGoogle Scholar
14. Fredsøe, J. & Deigaard, R. 1992 Mechanics of Coastal Sediment Transport. World Scientific.CrossRefGoogle Scholar
15. Fredsøe, J., Sumer, B. M., Laursen, T. S. & Pedersen, C. 1993 Experimental investigation of wave boundary layers with a sudden change in roughness. J. Fluid Mech. 252, 117–145.CrossRefGoogle Scholar
16. Fredsøe, J., Sumer, B. M., Kozakiewicz, A., Chua, L. H. C. & Deigaard, R. 2003 Effect of externally generated turbulence on wave boundary layer. Coast. Engng 49, 155–183.CrossRefGoogle Scholar
17. Fuhrman, D. R., Fredsøe, J. & Sumer, B. M. 2009 Bed slope effects on turbulent wave boundary layers: 2. Comparison with skewness, asymmetry and other effects. J. Geophys. Res. 114, C03025.CrossRefGoogle Scholar
18. Gonzalez-Rodriguez, D. & Madsen, O. S. 2007 Seabed shear stress and bedload transport due to asymmetric and skewed waves. Coast. Engng 54, 914–929.Google Scholar
19. Grass, A. J. 1971 Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 50, 233–255.CrossRefGoogle Scholar
20. Holmedal, L. E. & Myrhaug, D. 2006 Boundary layer flow and net sediment transport beneath asymmetrical waves. Cont. Shelf Res. 26 (2), 252–268.CrossRefGoogle Scholar
21. Hsu, T.-J. & Hanes, D. M. 2004 Effects of wave shape on sheet flow sediment transport. J. Geophys. Res. 109, C05025.CrossRefGoogle Scholar
22. Jensen, B. L., Sumer, B. M. & Fredsøe, J. 1989 Turbulent oscillatory boundary layers at high reynolds numbers. J. Fluid Mech. 206, 265–297.Google Scholar
23. Jonsson, I. G. 1963 Proc. 10th Congress IAHR, London, vol. 1, pp. 85–92.Google Scholar
24. Jonsson, I. G. 1980 A new approach to oscillatory rough turbulent boundary layers. Ocean Engng 7, 109–152.CrossRefGoogle Scholar
25. Jonsson, I. G. & Carlsen, N. A. 1976 Experimental and theoretical investigations in an oscillatory turbulent boundary layer. J. Hydraul Res. 14, 45–60.Google Scholar
26. Keane, R. D. & Adrian, R. D. 1992 Theory of cross-correlation analysis of PIV images. Appl. Sci. Res. 49, 191–215.CrossRefGoogle Scholar
27. Keiller, D. C. & Sleath, J. F. A. 1976 Velocity measurements close to a rough plate oscillating in its own plane. J. Fluid Mech. 73, 673–691.CrossRefGoogle Scholar
28. Kemp, P. H. & Simons, R. R. 1982 The interaction of waves with a turbulent current: waves propagating with the current. J. Fluid Mech. 116, 227–250.Google Scholar
29. Kemp, P. H. & Simons, R. R. 1983 The interaction of waves with a turbulent current: waves propagating against the current. J. Fluid Mech. 130, 73–89.CrossRefGoogle Scholar
30. Krstic, R. V. & Fernando, H. J. S. 2001 The nature of rough-wall oscillatory boundary layers. J. Hydraul. Res. 39, 655–666.CrossRefGoogle Scholar
31. Mirfenderesk, H. & Young, I. R. 2003 Direct measurements of the bottom friction factor beneath surface gravity waves. Appl. Ocean Res. 25, 269–287.CrossRefGoogle Scholar
32. Nielsen, P. 1992 Coastal Bottom Boundary Layers and Sediment Transport. World Scientific.CrossRefGoogle Scholar
33. O’Donoghue, T. & Wright, S. 2004 Flow tunnel measurements of velocities and sand flux in oscillatory sheet flow for well-sorted and graded sands. Coast. Engng 51, 1163–1184.Google Scholar
34. Ranasoma, K. & Sleath, J. 1992 Velocity measurements close to rippled beds. In Proc. 23rd Intl Conf. on Coastal Engng (ed. Edge, Billy L. ), pp. 2383–2396. ASCE.Google Scholar
35. Ribberink, J. S. & Al-Salem, A. A. 1994 Sediment transport in oscillatory boundary layers in cases of rippled beds and sheet flow. J. Geophys. Res. 99 (C6), 12707–12727.Google Scholar
36. Ribberink, J. S. & Al-Salem, A. A. 1995 Sheet flow and suspension of sand in oscillatory boundary layers. Coast. Engng 25, 205–225.CrossRefGoogle Scholar
37. Silva, P. A., Temperville, A. & Seabra-Santos, F. 2006 Sand transport under combined current and wave conditions: a semi-unsteady, practical model. Coast. Engng 53, 897–913.CrossRefGoogle Scholar
38. Sleath, J. F. A. 1970 Velocity measurements close to the bed in a wave tank. J. Fluid Mech. 42, 111–123.CrossRefGoogle Scholar
39. Sleath, J. F. A. 1987 Turbulent oscillatory flow over rough beds. J. Fluid Mech. 182, 369–409.Google Scholar
40. Soulsby, R. L. 1983 The bottom boundary layer of shelf seas. In Physical Oceanography of Coastal and Shelf Seas (ed. Johns, B. ), pp. 189–266. Elsevier.Google Scholar
41. Sumer, B. M., Laursen, T. S. & Fredsøe, J. 1993 Wave boundary layers in a convergent tunnel. Coast. Engng 20, 317–342.CrossRefGoogle Scholar
42. Swart, D. H. 1974 Offshore sediment transport and equilibrium beach profiles. In Publication No. 131. Delft Hydraulics Laboratory.Google Scholar
43. Trowbridge, J. & Madsen, O. S. 1984 Turbulentwave boundary layers 2. Second-order theory and mass transport. J. Geophys. Res. 89 (C5), 7999–8007.CrossRefGoogle Scholar
44. Watanabe, A. & Sato, S. 2004 A sheet-flow transport rate formula for asymmetric forward-leaning waves and currents. In Proc. 29th Intl Conf. on Coastal Engng (ed. McKee Smith, J. ). World Scientific.Google Scholar
45. Westergaard, C. H., Madsen, B. B., Marassi, M. & Tomasini, E. P. 2003 Accuracy of PIV signals in theory and practice. In 5th Intl Symp. on Particle Image Velocimetry, Busan, Korea, Paper 3301.Google Scholar
46. Westerweel, J. 1994 Efficient detection of spurious vectors in particle image velocimetry data. Exp. Fluids 16, 236–274.Google Scholar
47. Westerweel, J., Dabiri, D. & Gharib, M. 1997 The effect of a discrete window offset on the accuracy of cross-correlation analysis of digital piv recordings. Exp. Fluids 23, 20–28.Google Scholar