Published online by Cambridge University Press: 26 March 2024
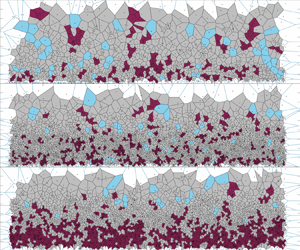
Based on Voronoi analysis, the properties related to the near-wall motion of particles in a turbulent boundary layer were experimentally investigated via different release modes, with a friction Reynolds number  $Re_\tau =3530$. For high-inertia sand particles with Stokes number
$Re_\tau =3530$. For high-inertia sand particles with Stokes number  $St^+ \sim O(10^2\unicode{x2013}10^3)$ and a volume fraction
$St^+ \sim O(10^2\unicode{x2013}10^3)$ and a volume fraction  $\varPhi _v \sim O(10^{-4})$, particle image tracking velocimetry was used to determine the particle position and near-wall distribution properties. We established three particle release modes, including top-released, bottom overall-released and bottom partially released sand particles, under the same flow field conditions and calculated the differences in particle near-wall clustering and void properties. It was confirmed that wall effects (including collision and strike-splash) have a great influence on particle clustering and void behaviour near the wall. In the top-released sand particle and locally laid sand particle cases, particles bounced off the smooth walls and re-entered the carrier flow, causing significant clustering and sparsing of particles near the walls. In contrast, in the overall sand-laying case where the bottom wall was completely covered with sand particles, there is no apparent cluster or void phenomenon near the wall
$\varPhi _v \sim O(10^{-4})$, particle image tracking velocimetry was used to determine the particle position and near-wall distribution properties. We established three particle release modes, including top-released, bottom overall-released and bottom partially released sand particles, under the same flow field conditions and calculated the differences in particle near-wall clustering and void properties. It was confirmed that wall effects (including collision and strike-splash) have a great influence on particle clustering and void behaviour near the wall. In the top-released sand particle and locally laid sand particle cases, particles bounced off the smooth walls and re-entered the carrier flow, causing significant clustering and sparsing of particles near the walls. In contrast, in the overall sand-laying case where the bottom wall was completely covered with sand particles, there is no apparent cluster or void phenomenon near the wall  $(z/\delta <0.12)$ and the particles are randomly distributed, due to the combined effect of particle impact and splashing. In addition, the clustering and voids of particles become more pronounced with increasing wall-normal distance in the three release modes, and the particle distribution shows some self-similarity at each flow layer. The probability density function of the concentration of cluster particles decreases following a ‘
$(z/\delta <0.12)$ and the particles are randomly distributed, due to the combined effect of particle impact and splashing. In addition, the clustering and voids of particles become more pronounced with increasing wall-normal distance in the three release modes, and the particle distribution shows some self-similarity at each flow layer. The probability density function of the concentration of cluster particles decreases following a ‘ $-5/3$’ power law. However, due to the particle–wall interaction, the probability density function gradually deviates from the ‘
$-5/3$’ power law. However, due to the particle–wall interaction, the probability density function gradually deviates from the ‘ $-5/3$’ power law.
$-5/3$’ power law.