Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T07:25:02.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of particle-driven secondary flow in turbulent pipe flows

Published online by Cambridge University Press:  24 August 2012

R. J. Belt ,
A. C. L. M. Daalmans  and
L. M. Portela
R. J. Belt
Affiliation:
Multi-Scale Physics Department, J. M. Burgerscentrum for Fluid Mechanics, Delft University of Technology, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands
A. C. L. M. Daalmans
Affiliation:
Multi-Scale Physics Department, J. M. Burgerscentrum for Fluid Mechanics, Delft University of Technology, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands
L. M. Portela*
Affiliation:
Multi-Scale Physics Department, J. M. Burgerscentrum for Fluid Mechanics, Delft University of Technology, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In fully developed single-phase turbulent flow in straight pipes, it is known that mean motions can occur in the plane of the pipe cross-section, when the cross-section is non-circular, or when the wall roughness is non-uniform around the circumference of a circular pipe. This phenomenon is known as secondary flow of the second kind and is associated with the anisotropy in the Reynolds stress tensor in the pipe cross-section. In this work, we show, using careful laser Doppler anemometry experiments, that secondary flow of the second kind can also be promoted by a non-uniform non-axisymmetric particle-forcing, in a fully developed turbulent flow in a smooth circular pipe. In order to isolate the particle-forcing from other phenomena, and to prevent the occurrence of mean particle-forcing in the pipe cross-section, which could promote a different type of secondary flow (secondary flow of the first kind), we consider a simplified well-defined situation: a non-uniform distribution of particles, kept at fixed positions in the ‘bottom’ part of the pipe, mimicking, in a way, the particle or droplet distribution in horizontal pipe flows. Our results show that the particles modify the turbulence through ‘direct’ effects (associated with the wake of the particles) and ‘indirect’ effects (associated with the global balance of momentum and the turbulence dynamics). The resulting anisotropy in the Reynolds stress tensor is shown to promote four secondary flow cells in the pipe cross-section. We show that the secondary flow is determined by the projection of the Reynolds stress tensor onto the pipe cross-section. In particular, we show that the direction of the secondary flow is dictated by the gradients of the normal Reynolds stresses in the pipe cross-section, 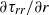and 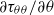. Finally, a scaling law is proposed, showing that the particle-driven secondary flow scales with the root of the mean particle-forcing in the axial direction, allowing us to estimate the magnitude of the secondary flow.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 709 , 25 October 2012 , pp. 1 - 36
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Absil, L. H. J. 1995 Analysis of the laser Doppler measurement technique for application in turbulent flows. PhD thesis, Delft University of Technology.Google Scholar
2. Belt, R. J. 2007 On the liquid film in inclined annular flow. PhD thesis, Delft University of Technology.Google Scholar
3. Benedict, L. H., Nobach, H. & Tropea, C. 2000 Estimation of turbulent velocity spectra from laser Doppler data. Meas. Sci. Technol. 11 (8), 1089–1104.Google Scholar
4. Boivin, M., Simonin, O. & Squires, K. D. 1998 Direct numerical simulation of turbulence modulation by particles in isotropic turbulence. J. Fluid Mech. 375, 235–263.Google Scholar
5. Brundrett, E. & Baines, W. D. 1964 The production and diffusion of vorticity in duct flow. J. Fluid Mech. 19 (3), 375–394.Google Scholar
6. Daalmans, A. C. L. M. 2005 Laser Doppler anemometry measurements of particle-driven secondary flow in turbulent horizontal pipe flow. MSc thesis, Delft University of Technology.Google Scholar
7. Darling, R. S. & McManus, H. N. 1968 Flow patterns in circular ducts with circumferential variation of roughness: a two-phase flow analog. Dev. in Mech.: Proc. 11th Midwestern Mech. Conf. 5, 153–163.Google Scholar
8. Demuren, A. O. & Rodi, W. 1984 Calculation of turbulence-driven secondary motion in non-circular ducts. J. Fluid Mech. 140, 189–222.CrossRefGoogle Scholar
9. Dykhno, L. A., Williams, L. R. & Hanratty, T. J. 1994 Maps of mean gas velocity for stratified flows with and without atomization. Intl J. Multiphase Flow 20 (4), 691–702.Google Scholar
10. Eggels, J. G. M., Unger, F., Weiss, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–209.CrossRefGoogle Scholar
11. Flores, A. G., Crowe, K. E. & Griffith, P. 1995 Gas-phase secondary flow in horizontal, stratified and annular two-phase flow. Intl J. Multiphase Flow 21 (2), 207–221.CrossRefGoogle Scholar
12. Hallez, Y. & Magnaudet, J. 2009 Turbulence-induced secondary motion in a buoyancy-driven flow in a circular pipe. Phys. Fluids 21, 081704.Google Scholar
13. Harteveld, W. K. 2005 Bubble columns: structures or stability? PhD thesis, Delft University of Technology.Google Scholar
14. Hinze, J. O. 1973 Experimental investigation on secondary currents in the turbulent flow through a straight conduit. Appl. Sci. Res. 28, 453–465.Google Scholar
15. Huber, N. & Sommerfeld, M. 1998 Modelling and numerical calculation of dilute-phase pneumatic conveying in pipe systems. Powder Technol. 99, 90–101.Google Scholar
16. Launder, B. E. & Ying, W. M. 1972 Secondary flows in ducts of square cross-section. J. Fluid Mech. 54 (2), 289–295.CrossRefGoogle Scholar
17. Li, Y., McLaughlin, J. B., Kontomaris, K. & Portela, L. 2001 Numerical simulation of particle-laden turbulent channel flow. Phys. Fluids 13 (10), 2957–2967.Google Scholar
18. Liné, A., Masbernat, L. & Soualmia, A. 1994 Interfacial interactions and secondary flows in stratified two-phase flow. Chem. Engng Commun. 141–142, 303–329.Google Scholar
19. Nagata, K., Hunt, J. C. R., Sakai, Y. & Wong, H. 2011 Distorted turbulence and secondary flow near right-angled plates. J. Fluid Mech. 668, 446–479.CrossRefGoogle Scholar
20. Nobach, H. 2002 Local time estimation for the slotted correlation function of randomly sampled LDA data. Exp. Fluids 32 (3), 337–345.Google Scholar
21. Nordsveen, M. 2001 Wave- and turbulence-induced secondary currents in the liquid phase in stratified duct flow. Intl J. Multiphase Flow 27 (9), 1555–1577.CrossRefGoogle Scholar
22. Portela, L. M., Cota, P. & Oliemans, R. V. A. 2002 Numerical study of the near-wall behaviour of particles in turbulent pipe flows. Powder Technol. 125 (2–3), 149–157.CrossRefGoogle Scholar
23. Speziale, C. G. 1982 On turbulent secondary flows in pipes of noncircular cross-section. Intl J. Engng Sci. 20 (7), 863–872.CrossRefGoogle Scholar
24. Squires, K. D. & Eaton, J. K. 1990 Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A 2, 1191–1203.Google Scholar
25. Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
26. Tummers, M. J. 1999 Investigation of a turbulent wake in an adverse pressure-gradient using laser Doppler anemometry. PhD thesis, Delft University of Technology.Google Scholar
27. Van Maanen, H. R. E. 1999 Retrieval of turbulence and turbulence properties from randomly sampled laser-Doppler anemometry data with noise. PhD thesis, Delft University of Technology.Google Scholar
28. Van’t Westende, J. M. C., Belt, R. J., Portela, L. M., Mudde, R. F. & Oliemans, R. V. A. 2007 Effect of secondary flow on droplet distribution and deposition in horizontal annular pipe flow. Intl J. Multiphase Flow 33 (1), 67–85.Google Scholar