Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T20:27:48.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of the wave-induced motion of and force distribution along a flexible stem

Published online by Cambridge University Press:  18 October 2019

Niels G. Jacobsen Open the ORCID record for Niels G. Jacobsen [Opens in a new window] ,
Wout Bakker ,
Wim S. J. Uijttewaal  and
Rob Uittenbogaard
Niels G. Jacobsen*
Affiliation:
Harbour, Coastal and Offshore, Deltares, 2629HV Delft, The Netherlands
Wout Bakker
Affiliation:
Numerical Simulation Software, Deltares, 2629HV Delft, The Netherlands EcoFlows, 1015BL Amsterdam, The Netherlands
Wim S. J. Uijttewaal
Affiliation:
Environmental Fluid Mechanics, Hydraulic Engineering, Delft University of Technology, 2628CN Delft, The Netherlands
Rob Uittenbogaard
Affiliation:
Numerical Simulation Software, Deltares, 2629HV Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The work presents an experimental investigation into the motion of and hydrodynamic forces along a single flexible stem in regular waves. The experiment covers a large range in relevant non-dimensional parameters: the drag-to-stiffness ratio 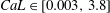$CaL\in [0.003,3.8]$, the inertia-to-stiffness ratio 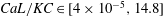$CaL/KC\in [4\times 10^{-5},14.8]$, the Keulegan–Carpenter number 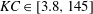$KC\in [3.8,145]$ and the Reynolds number 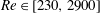$Re\in [230,2900]$. The two first parameters relate to the response of the stem in waves and thus account for material properties, while the two last parameters are relevant for hydrodynamic forces on the stem. The displacement of the stem was captured with a digital video camera and the displacement along the stem was captured for every 2.5 mm at 25 Hz. This unique laboratory data set allowed for the following analyses: (i) Determination of the relevant non-dimensional parameter to predict the stem motion and shape. (ii) A direct comparison between the measured force for mimics of two lengths (0.15 m and 0.30 m) illustrating the force reduction potential for flexible mimics. (iii) Direct evaluation of the average force coefficients 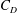$C_{D}$ (drag) and 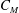$C_{M}$ (inertia) for the flexible stems. (iv) The distributed external hydrodynamic loading and the internal shear forces were estimated from the laboratory experiments. The distribution of the shear force helped to understand the breakage mechanisms of flexible stems. (v) A linkage between phase lags and internal shear forces was suggested. The data set is considered valuable as validation material for numerical models of stem motion in waves.

JFM classification

Geophysical and Geological Flows: Coastal engineering
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 1036 - 1069
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdolahpour, M., Hambleton, M. & Ghisalberti, M. 2017 The wave-driven current in coastal canopies. J. Geophys. Res.: Oceans 122, 1–15.Google Scholar
Anderson, M. E. & Smith, J. M. 2014 Wave attenuation by flexible, idealized salt marsh vegetation. Coast. Engng 83, 82–92.Google Scholar
Birkemeier, W. A. 1984 Time scales of nearshore profile changes. Proc. Coast. Engng Conf. II, 1507–1521.Google Scholar
Bradley, K. & Houser, C. 2009 Relative velocity of seagrass blades: implications for wave attenuation in low-eenrgy environments. J. Geophys. Res. 114, 1–13.Google Scholar
Chen, H. & Zou, Q.-P. 2019 Eulerian-Lagrangian flow-vegetation interaction model using immersed boundary method and OpenFOAM. Adv. Water Resour. 126, 176–192.Google Scholar
Conzalez-Cruz, C. A., Jauregui-Correa, J. C. & Herrera-Ruiz, G. 2016 Nonlinear response of cantilever beams due to large geometric deformations: experimental validation. J. Mech. Engng 62 (3), 187–196.Google Scholar
Dean, R. G. & Bender, C. J. 2006 Static wave setup with emphasis on damping effects by vegetation and bottom friction. Coast. Engng 53, 149–156.Google Scholar
Deigaard, R. & Fredsøe, J. 1989 Shear-stress distribution in dissipative water-waves. Coast. Engng 13 (4), 357–378.Google Scholar
Deigaard, R., Justesen, P. & Fredsøe, J. 1991 Modeling of undertow by a one-equation turbulence model. Coast. Engng 15 (5–6), 431–458.Google Scholar
Dijkstra, J. T. & Uittenbogaard, R. E. 2010 Modeling the interaction between flow and highly flexible aquatic vegetation. Water Resour. Res. 46, W12547, 14 pages.Google Scholar
Dubi, A. & Tørum, A. 1994 Wave damping by kelp vegetation. Proc. Coast. Engng Conf. I, 142–156.Google Scholar
EurOtop 2018 Manual on wave overtopping of sea defences and related structures. An overtopping manual largely based on European research, but for worldwide application. Van der Meer, J. W., Allsop, N. W. H., Bruce, T., De Rouck, J., Kortenhaus, A., Pullen, T., Schüttrumpf, H., Troch, P. and Zanuttigh, B. Available at: www.overtopping-manual.com.Google Scholar
Foster-Martinez, M. R., Lacy, J. R., Ferner, M. C. & Variano, E. A. 2018 Wave attenuation across a tidal march in San Francisco Bay. Coast. Engng 138, 26–40.Google Scholar
Gijón Mancheño, A.2016 Interaction between wave hydrodynamics and flexible vegetation. Master’s thesis, Delft University of Technology.Google Scholar
Guannel, G. & Özkan-Haller, H. T. 2014 Formulation of the undertow using linear wave theory. Phys. Fluids 26, 1–18.Google Scholar
Heideman, J. C. & Sarpkaya, T. 1985 Hydrodynamic forces on dense arrays of cylinders. In Offshore Technology Conference, pp. 421–428. Offshore Technology Conference.Google Scholar
Jacobsen, N. G., McFall, B. C. & van der A, D. A. 2019 A frequency distributed dissipation model for canopies. Coast. Engng 150, 135–146.Google Scholar
Jacobsen, N. G., van Velzen, G. & Fredsøe, J. 2014 Analysis of pile scour and associated hydrodynamic forces using proper orthogonal decomposition. In Scour and Erosion: Proceedings of the 7th International Conference on Scour and Erosion, Perth, Australia, 2–4 December 2014, p. 361. CRC Press.Google Scholar
Jadhav, R. S., Chen, Q. & Smith, J. M. 2013 Spectral distribution of wave energy dissipation by salt marsh vegetation. Coast. Engng 77, 99–107.Google Scholar
Leclercq, T. & De Langre, E. 2018 Reconfiguration of elastic blades in oscillatory flow. J. Fluid Mech. 838, 606–630.Google Scholar
Lei, J. & Nepf, H. 2019 Wave damping by flexible vegetation: connecting individual blade dynamics to the meadow scale. Coast. Engng 147, 138–148.Google Scholar
Losada, I. J., Maza, M. & Lara, J. L. 2016 A new formulation for vegetation-induced damping under combined waves and currents. Coast. Engng 107, 1–13.Google Scholar
Luhar, M., Coutu, S., Infantes, E., Fox, S. & Nepf, H. 2010 Wave-induced velocities inside a model seagrass bed. J. Geophys. Res. 115 (C12005), 1–15.Google Scholar
Luhar, M. & Nepf, H. 2011 Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 56 (6), 2003–2017.Google Scholar
Luhar, M. & Nepf, H. M. 2016 Wave-induced dynamics of flexible blades. J. Fluids Struct. 61, 20–41.Google Scholar
Maza, M., Lara, J. L. & Losada, I. J. 2013 A coupled model of submerged vegetation under oscillatory flow using Navier–Stokes equations. Coast. Engng 80, 16–34.Google Scholar
Maza, M., Lara, J. L., Losada, I. J., Ondiviela, B., Trinogga, J. & Bouma, T. J. 2015 Large-scale 3-D experiments of wave and current interaction with real vegetation. Part 2: experimental analysis. Coast. Engng 106, 73–86.Google Scholar
Möller, I, Kudella, M., Rupprecht, F., Spencer, T., Paul, M., Van Wesenbeeck, B. K., Wolters, G., Jensen, K., Bouma, T. J., Miranda-Lange, M. & Schimmels, S. 2014 Wave attenuation over coastal salt marches under storm surge conditions. Nature Geosci. 7, 727–731.Google Scholar
Mullarney, J. C. & Henderson, S. M. 2010 Wave-forced motion of submerged single-stem vegetation. J. Geophys. Res. 115, C12061.Google Scholar
Mullarney, J. C. & Pilditch, C. A. 2017 The differential response of kelp to swell and infragravity wave motion. Limnol. Oceanogr. 62 (6), 2524–2537.Google Scholar
Pujol, D., Serra, T., Colomer, J. & Casamitjana, X. 2013 Flow structure in canopy models dominated by progressive waves. J. Hydrol. 486, 281–292.Google Scholar
Ros, A., Colomer, J., Serra, T., Pujol, D., Soler, M. & Casamitjana, X. 2014 Experimental observations on sediment resuspension within submerged model canopies under oscillatory flow. Cont. Shelf Res. 91, 220–231.Google Scholar
Ruessink, B. G., Ramaekers, G. & Van Rijn, L. C. 2012 On the parameterization of the free-stream non-linear wave orbital motion in nearshore morphodynamic models. Coast. Engng 65, 56–63.Google Scholar
Sarpkaya, T. 1979 Hydrodynamic forces on various multiple-tube riser configurations. Offshore Technol. Conf. 1603–1606.Google Scholar
Sumer, B. M. & Fredsøe, J. 1999 Hydrodynamics around Cylindrical Structures, 1st edn. Advanced Series on Coastal Engineering, vol. 12. World Scientific.Google Scholar
Suzuki, T., Zijlema, M., Burger, B., Meijer, M. C. & Narayan, S. 2012 Wave dissipation by vegetation with layer schematization in SWAN. Coast. Engng 59, 64–71.Google Scholar
Tinoco, R. O. & Coco, G. 2018 Turbulence as the main driver of resuspension in oscillatory flow through vegetation. J. Geophys. Res. Earth Surf. 123, 1–14.Google Scholar
Van Rooijen, A. A., McCall, R. T., Van Thiel de Vries, J. S. M., Van Dongeren, A. R., Reniers, A. J. H. M. & Roelvink, J. A. 2016 Modeling the effect of wave-vegetation interaction on wave setup. J. Geophys. Res. Oceans 121, 1–19.Google Scholar
Vo-Luong, P. & Massel, S. 2008 Energy dissipation in non-uniform mangrove forests of arbitrary depth. J. Mar. Syst. 74 (1), 603–622.Google Scholar
Vuik, V., Van Vuren, S., Borsje, B. W., Van Wesenbeeck, B. K. & Jonkmann, S. N. 2018 Assessing satefy of nature-based flood defenses: Dealing with extremes and uncertainties. Coast. Engng 139, 47–64.Google Scholar
Wu, W., Ozeren, Y., Chen, Q., Holland, M., Ding, Y., Kuiry, S. N., Zhang, M., Jadhav, R., Chatagnier, J., Chen, Y. & Gordji, L.2011 Phase I report for SERRI project no. 80037: investigation of surge and wave reduction by vegetation. Tech. Rep. 80037-01. National Center for Computational Hydroscience and Engineering; The University of Mississippi.Google Scholar
Zeller, R. B., Weitzman, J. S., Abbett, M. E., Zarama, F. J., Fringer, O. B. & Koseff, J. R. 2014 Improved parameterization of seagrass blade dynamics and wave attenuation based on numerical and laboratory experiments. Limnol. Oceanogr. 59 (1), 251–266.Google Scholar
Zhang, Y. & Nepf, H. 2019 Wave-driven sediment resuspension within a model eelgrass meadow. J. Geophys. Res. Earth Surf. 124, 1–19.Google Scholar
Zhu, L., Chen, Q., Ding, Y., Jafari, N. & Rosati, J. D. 2019 Semianalytical model of depth-integrated vegetal drag force based on Stokes second-order wave theory. ASCE J. Waterway Port Coastal Ocean Engng 145 (2), 1–13.Google Scholar

Jacobsen et al. supplementary movie 1

Movie of the stem motion for mimic 2 with $H = 0.04$ m, $T = 2.0$ s and $l = 0.30$ m. The waves propagate from left to right. Top-left panel: Stem and relative velocities; 1.0 m corresponds to 1.0 m/s. Top-right panel: The distributed hydrodynamic force. Bottom-left panel: Stem and relative accelerations; 0.2 m corresponds to 1.0 m/s${}^2$. Bottom-right panel: The internal shear force.

Download Jacobsen et al. supplementary movie 1(Video)
Video 16.6 MB

Jacobsen et al. supplementary movie 2

Movie of the stem motion for mimic 2 with $H = 0.11$ m, $T = 3.0$ s and $l = 0.30$ m. The waves propagate from left to right. Top-left panel: Stem and relative velocities; 0.4 m corresponds to 1.0 m/s. Top-right panel: The distributed hydrodynamic force. Bottom-left panel: Stem and relative accelerations; 0.1 m corresponds to 1.0 m/s${}^2$. Bottom-right panel: The internal shear force.

Download Jacobsen et al. supplementary movie 2(Video)
Video 24.4 MB

Jacobsen et al. supplementary movie 3

Movie of the stem motion for mimic 3 with $H = 0.04$ m, $T = 2.0$ s and $l = 0.30$ m. The waves propagate from left to right. Top-left panel: Stem and relative velocities; 1.0 m corresponds to 1.0 m/s. Top-right panel: The distributed hydrodynamic force. Bottom-left panel: Stem and relative accelerations; 0.2 m corresponds to 1.0 m/s${}^2$. Bottom-right panel: The internal shear force.

Download Jacobsen et al. supplementary movie 3(Video)
Video 15.8 MB

Jacobsen et al. supplementary movie 4

Movie of the stem motion for mimic 3 with $H = 0.11$ m, $T = 3.0$ s and $l = 0.30$ m. The waves propagate from left to right. Top-left panel: Stem and relative velocities; 0.5 m corresponds to 1.0 m/s. Top-right panel: The distributed hydrodynamic force. Bottom-left panel: Stem and relative accelerations; 0.1 m corresponds to 1.0 m/s${}^2$. Bottom-right panel: The internal shear force.

Download Jacobsen et al. supplementary movie 4(Video)
Video 25.9 MB