Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-04T21:59:41.752Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of freely falling thin disks. Part 2. Transition of three-dimensional motion from zigzag to spiral

Published online by Cambridge University Press:  30 August 2013

Cunbiao Lee ,
Zhuang Su ,
Hongjie Zhong ,
Shiyi Chen ,
Mingde Zhou  and
Jiezhi Wu
Cunbiao Lee*
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Zhuang Su
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Hongjie Zhong
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Shiyi Chen
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Mingde Zhou
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Jiezhi Wu
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

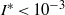The free-fall motion of a thin disk with small dimensionless moments of inertia (${I}^{\ast } \lt 1{0}^{- 3} $) was investigated experimentally. The transition from two-dimensional zigzag motion to three-dimensional spiral motion occurs due to the growth of three-dimensional disturbances. Oscillations in the direction normal to the zigzag plane increase with the development of this instability. At the same time, the oscillation of the nutation angle decreases to zero and the angle remains constant. The effects of initial conditions (release angle) were investigated. Two kinds of transition modes, zigzag–spiral transition and zigzag–spiral–zigzag intermittence transition, were observed to be separated by a critical Reynolds number. In addition, the solution of the generalized Kirchhoff equations shows that the small 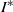${I}^{\ast } $ is responsible for the growth of disturbances in the third dimension (perpendicular to the planar motion).

JFM classification

Aerodynamics: Aerodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , pp. 77 - 104
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, A., Pesavento, U. & Wang, Z. J. 2005 Unsteady dynamics of fluttering and tumbling plates. J. Fluid Mech. 541, 65–90.CrossRefGoogle Scholar
Belmonte, A., Eisenberg, H. & Moses, E. 1998 From flutter to tumble: inertial drag and Froude similarity in falling paper. Phys. Rev. Lett. 81, 345–348.Google Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2013 Numerical simulation of the dynamics of freely falling discs. Phys. Fluids 25, 044102.CrossRefGoogle Scholar
Ern, P., Fernandes, P. C., Risso, F. & Magnaudet, J. 2007 Evolution of the wake structure and wake induced-loads along the path of free rising axisymetric bodies. Phys. Fluids 17, 113302.CrossRefGoogle Scholar
Ern, P., Risso, F., Fernandes, P. C. & Magnaudet, J. 2009 Dynamical model for the bouyancy-driven zigzag motion of oblate bodies. Phys. Rev. Lett. 102, 134505.Google Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2005 On the zigzag dynamics of freely moving axisymetric bodies. Phys. Fluids 17, 098107.CrossRefGoogle Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2008 Dynamics of axisymetric bodies rising along a zigzag path. J. Fluid Mech. 606, 209–223.CrossRefGoogle Scholar
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetry bodis. J. Fluid Mech. 573, 479–502.Google Scholar
Fields, S., Klaus, M., Moore, M. & Nori, F. 1997 Chaotic dynamics of falling disks. Nature 388, 252–254.CrossRefGoogle Scholar
Franck, A., Jacques, M. & David, F. 2013 Falling styles of disks. J. Fluid Mech. 719, 388–405.Google Scholar
Horowitz, M. & Williamson, C. H. K. 2008 Critical mass and a new periodic four-ring vortex wake mode for freely rising and falling sphere. Phys. Fluids 20, 101701.CrossRefGoogle Scholar
Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.Google Scholar
Howe, M. 1995 On the force and moment on a body in an imcompressible fluid, with application to rigid bodies and bubbles at high and low Reynolds numbers. Q. J. Mech. Appl. Maths 48, 401–426.CrossRefGoogle Scholar
Lee, C. B., Peng, H. W., Yuan, H. J., Wu, J. Z., Zhou, M. D. & Hussain, F. 2011 Experimental studies of surface waves inside a cylindrical container. J. Fluid Mech. 677, 39–62.Google Scholar
Lee, C. B. & Wu, J. Z. 2008 Transition in wall bounded flow. Appl. Mech. Rev. 61, 030802.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomegeneous flow. Annu. Rev. Fluid Mech. 32, 659–708.CrossRefGoogle Scholar
Mahadevan, L., Ryu, W. S. & Samuel, A. D. T. 1999 Tumbling cards. Phys. Fluids 11, 1–3.Google Scholar
Mougin, G. & Magnaudet, J. 2002a The generalized Kirchhoff equations and their application to the interaction between a rigid body and an arbitrary time-dependent viscous flow. Intl J. Multiphase Flow 28, 1837–1851.CrossRefGoogle Scholar
Mougin, G. & Magnaudet, J. 2002b Path instability of a rising bubble. Phys. Rev. Lett. 88, 014502.Google Scholar
Mougin, G. & Magnaudet, J. 2006 Wake-induced forces and torques on a zigzag/spiralling bubble. J. Fluid Mech. 567, 185–194.Google Scholar
Pesavento, U. & Wang, Z. J. 2004 Falling paper: Navier–Stokes solutions, model of fluid forces, and centre of mass elevation. Phys. Rev. Lett. 93, 144501.Google Scholar
Saffman, P. G. 1956 On the rise of small air bubbles in water. J. Fluid Mech. 1, 249–275.Google Scholar
Shew, W. L. & Pinton, J. F. 2006 Dynamical model of bubble path instability. Phys. Rev. Lett. 97, 144508.Google Scholar
Smith, E. H. 1971 Autorotating wings: an experimental investigation. J. Fluid Mech. 50, 513–534.Google Scholar
Stewart, R. E. & List, R. 1983 Gyrational motion of disks during free-fall. Phys. Fluids 26, 920–927.Google Scholar
Stringham, G. E., Simons, D. B. & Guy, H. P. 1969 The behaviour of large particles falling in quiescent liquids. US Geological Survey.Google Scholar
Vandenberghe, N., Zhang, J. & Childress, S. 2004 Symmetry breaking leads to forward flapping flight. J. Fluid Mech. 506, 147–155.Google Scholar
Willmarth, W. W., Hawk, N. E. & Harvey, R. L. 1964 Steady and unsteady motions and wakes of freely-falling disks. Phys. Fluids 7, 197–208.CrossRefGoogle Scholar
Zhong, H. J., Chen, S. Y. & Lee, C. B. 2011 Experimental investigation of freely falling thin disks: transition from zigzag to spiral. Phys. Fluids 23, 9–12.Google Scholar
Zhong, H. J., Lee, C. B., Su, Z., Chen, S. Y., Zhou, M. D. & Wu, J. Z. 2012 Experimental investigation of freely falling thin disks. Part 1. The flow structures and Reynolds number effects on the zigzag motion. J. Fluid Mech. 716, 228–250.Google Scholar