Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T20:50:55.355Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of freely falling thin disks. Part 1. The flow structures and Reynolds number effects on the zigzag motion

Published online by Cambridge University Press:  25 January 2013

Hongjie Zhong ,
Cunbiao Lee ,
Zhuang Su ,
Shiyi Chen ,
Mingde Zhou  and
Jiezhi Wu
Hongjie Zhong*
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China Aero Science Key Lab of High Reynolds Aerodynamics Force at High Speed, AVIC Aerodynamics Research Institute, Shenyang, 110034, China
Cunbiao Lee
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Zhuang Su
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Shiyi Chen
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Mingde Zhou
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
Jiezhi Wu
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing, 100871, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper describes an experimental investigation of the dynamics of a freely falling thin circular disk in still water. The flow patterns of the disk zigzag motion are studied using dye visualization and particle image velocimetry. Time-resolved disk motions with six degrees of freedom are obtained with a stereoscopic vision method. 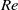The flow separation and vortex shedding are found to change with the Reynolds number, $\mathit{Re}$. At high Reynolds numbers a new dipole vortex is shed that is significantly different from Kármán-type vortices. The vortical structures are mainly composed of leading-edge vortices, a counter-rotating vortex pair and secondary trailing-edge vortices. The amplitude of the horizontal oscillation is also dependent on the Reynolds number with a critical Reynolds number ${\mathit{Re}}_{cr} \approx 2000$, where the oscillatory amplitude is proportional to 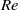$\mathit{Re}$ for 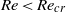$\mathit{Re}\lt {\mathit{Re}}_{cr} $, but becomes invariant for 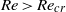$\mathit{Re}\gt {\mathit{Re}}_{cr} $. Three-dimensional dipolar vortices were also observed experimentally.

JFM classification

Aerodynamics: Aerodynamics Aerodynamics: Flow-structure interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 228 - 250
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, J. R. L. 1984 Experiments on the settling, overturning and entrainment of bivalve shells and related models. Sedimentology 31, 227–250.Google Scholar
Andersen, A., Pesavento, U. & Wang, Z. J. 2005a Analysis of transitions between fluttering, tumbling and steady descent of falling cards. J. Fluid Mech. 541, 91–104.CrossRefGoogle Scholar
Andersen, A., Pesavento, U. & Wang, Z. J. 2005b Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 541, 65–90.Google Scholar
Aref, H. & Jones, S. W. 1993 Chaotic motion of solid through ideal fluid. Phys. Fluids A 5, 3026–3028.CrossRefGoogle Scholar
Belmonte, A., Eisenberg, H. & Moses, E. 1998 From flutter to tumble: inertial drag and froude similarity in falling paper. Phys. Rev. Lett. 81, 345–348.Google Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2005 On the zigzag dynamics of freely moving axisymmetric bodies. Phys. Fluids 17, 098107.CrossRefGoogle Scholar
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetry bodies. J. Fluid Mech. 573, 479–502.Google Scholar
Fields, S., Klaus, M., Moore, M. & Nori, F. 1997 Chaotic dynamics of falling disks. Nature 388, 252–254.Google Scholar
Horowitz, M. & Williamson, C. H. K. 2008 Critical mass and a new periodic four-ring vortex wake mode for freely rising and falling spheres. Phys. Fluids 20, 101701.CrossRefGoogle Scholar
Isaacs, J. L. & Thodos, G. 1967 The free-settling of solid cylindrical particles in the turbulent regime. Can. J. Chem. Engng 45, 150–155.Google Scholar
Jones, M. A. & Shelley, M. J. 2005 Falling cards. J. Fluid Mech. 540, 393–425.CrossRefGoogle Scholar
Kry, P. R. & List, R. 1974 Angular motions of freely falling spheroidal hailstone models. Phys. Fluids 17, 1094–1102.Google Scholar
Lee, C. B., Peng, H. W., Yuan, H. J., Wu, J. Z., Zhou, M. D. & Hussain, F. 2011 Experimental studies of surface waves inside a cylindrical container. J. Fluid Mech. 677, 39–62.Google Scholar
List, R. & Schemenauer, R. S. 1971 Free-fall behaviour of planar snow crystals, conical graupel and small hail. J. Atmos. Sci 28, 110–115.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomegeneous flow. Annu. Rev. Fluid Mech. 32, 659–708.Google Scholar
Mahadevan, L., Ryu, W. S. & Samuel, A. D. T. 1999 Tumbling cards. Phys. Fluids 11, 1–3.Google Scholar
Maxwell, J. C. 1853 On a particular case of the descent of a heavy body in a resisting medium. Camb. Dublin Math. J. 9, 115–118.Google Scholar
McCutchen, C. W. 1977 The spinning rotation of ash and tulip tree samaras. Science 197, 691–692.Google Scholar
Newton, I. 1999 Philosophiae Naturalis Principia Mathematica, 3rd edn. University of California, translated by I. B. Cohen and A. Whitman.Google Scholar
Nobach, H. & Honkanen, M. 2005 Two-dimensional Gaussian regression for sub-pixel displacement estimation in particle image velocimetry or particle position estimation in particle tracking velocimetry. Exp. Fluids 38, 511–515.CrossRefGoogle Scholar
Pesavento, U. & Wang, Z. J. 2004 Falling paper: Navier–Stokes solutions, model of fluid forces, and centre of mass elevation. Phys. Rev. Lett. 93, 144501.Google Scholar
Saffman, P. G. 1956 On the rise of small air bubbles in water. J. Fluid Mech. 1, 249–275.Google Scholar
Scarano, F. & Riethmuller, M. 2000 Advances in iterative multigrid PIV image processing. Exp. Fluids Suppl. 29, S51–S60.Google Scholar
Shew, W. L., Poncet, S. & Pinto, J. F. 2006 Force measurement on rising bubbles. J. Fluid Mech. 569, 51–60.Google Scholar
Smith, E. H. 1971 Autorotating wings: an experimental investigation. J. Fluid Mech. 50, 513–534.CrossRefGoogle Scholar
Stewart, R. E. & List, R. 1983 Gyrational motion of disks during free-fall. Phys. Fluids 26, 920–927.Google Scholar
Stringham, G. E., Simons, D. B. & Guy, H. P. 1969 The behaviour of large particles falling in quiescent liquids. US Geol. Surv. Prof. Paper 562-c, 1.Google Scholar
Tanabe, Y. & Kaneko, K. 1994 Behavior of a falling paper. Phys. Rev. Lett. 73, 1372–1375.CrossRefGoogle ScholarPubMed
Tsai, R. Y. 1987 A versatile camera calibration technique for high accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 3, 323–344.CrossRefGoogle Scholar
Veldhuis, C. H. J. & Biesheuvel, A. 2007 An experimental study of the regimes of motion of spheres falling or ascending freely in a Newtonian fluid. Intl J Multiphase Flow 33, 1074–1087.Google Scholar
Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37, 183–210.CrossRefGoogle Scholar
Willmarth, W. W., Hawk, N. E. & Harvey, R. L. 1964 Steady and unsteady motions and wakes of freely falling disks. Phys. Fluids 7, 197–208.Google Scholar
Yaginuma, T. & Itō, H. 2008 Drag and wakes of freely falling $6{0}^{\circ } $ cones at intermediate Reynolds numbers. Phys. Fluids 20, 117102.Google Scholar
Zhang, Z. Y. 2000 A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 22, 1330–1334.Google Scholar
Zhong, H. J., Chen, S. Y. & Lee, C. B. 2011 Experimental investigation of freely falling thin disks: transition from zigzag to spiral. Phys. Fluids 23, 9–12.Google Scholar
Zhong, H. J. & Lee, C. B. 2009 Paths of freely falling disks. Mod. Phys. Lett. B 23, 373–376.Google Scholar
Zhong, H. J. & Lee, C. B. 2012 The wake of falling disks at low Reynolds numbers. Acta Mechanica Sin. 28 (2), 367–371.Google Scholar