Published online by Cambridge University Press: 29 April 2013
We present a detailed experimental investigation of conditional statistics obtained from dissipation elements based on the passive scalar field 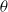 $\theta $ and its instantaneous scalar dissipation rate
$\theta $ and its instantaneous scalar dissipation rate 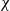 $\chi $. Using high-frequency planar Rayleigh scattering measurements of propane discharging as a round turbulent jet into coflowing carbon dioxide, we acquire with Taylor’s hypothesis a highly resolved three-dimensional field of the propane mass fraction
$\chi $. Using high-frequency planar Rayleigh scattering measurements of propane discharging as a round turbulent jet into coflowing carbon dioxide, we acquire with Taylor’s hypothesis a highly resolved three-dimensional field of the propane mass fraction 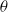 $\theta $. The Reynolds number (based on nozzle diameter and jet exit velocity) varies between 3000 and 8600. The experimental results for the joint probability density of the scalar difference
$\theta $. The Reynolds number (based on nozzle diameter and jet exit velocity) varies between 3000 and 8600. The experimental results for the joint probability density of the scalar difference 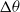 $ \mathrm{\Delta} \theta $ and the length
$ \mathrm{\Delta} \theta $ and the length 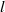 $l$ of dissipation elements resembles those previously obtained from direct numerical simulations of Wang & Peters (J. Fluid Mech., vol. 554, 2006, pp. 457–475). In addition, the normalized marginal probability density function
$l$ of dissipation elements resembles those previously obtained from direct numerical simulations of Wang & Peters (J. Fluid Mech., vol. 554, 2006, pp. 457–475). In addition, the normalized marginal probability density function 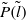 $\tilde {P} (\tilde {l} )$ of the length of dissipation elements follows closely the theoretical model derived by Wang & Peters (J. Fluid Mech., vol. 608, 2008, pp. 113–138). We also find that the mean linear distance
$\tilde {P} (\tilde {l} )$ of the length of dissipation elements follows closely the theoretical model derived by Wang & Peters (J. Fluid Mech., vol. 608, 2008, pp. 113–138). We also find that the mean linear distance 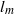 ${l}_{m} $ between two extreme points of an element is of the order of the scalar Taylor microscale
${l}_{m} $ between two extreme points of an element is of the order of the scalar Taylor microscale 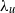 ${\lambda }_{u} $. Furthermore, the conditional mean
${\lambda }_{u} $. Furthermore, the conditional mean 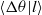 $\langle \mathrm{\Delta} \theta \vert l\rangle $ scales with Kolmogorov’s
$\langle \mathrm{\Delta} \theta \vert l\rangle $ scales with Kolmogorov’s 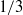 $1/ 3$ power law. The investigation of the orientation of long dissipation elements in the jet flow reveals a preferential alignment, perpendicular to the streamwise direction for long elements, while the orientation of short elements is close to isotropic. Following an approach proposed by Kholmyansky & Tsinober (Phys. Lett. A, vol. 373, 2009, pp. 2364–2367), we finally investigate the probability density function of the scalar increment
$1/ 3$ power law. The investigation of the orientation of long dissipation elements in the jet flow reveals a preferential alignment, perpendicular to the streamwise direction for long elements, while the orientation of short elements is close to isotropic. Following an approach proposed by Kholmyansky & Tsinober (Phys. Lett. A, vol. 373, 2009, pp. 2364–2367), we finally investigate the probability density function of the scalar increment 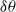 $\delta \theta $ in the streamwise direction, when strong dissipative events are either retained in or excluded from the measurement volume. In the present study, however, these events are related to maximum points of the scalar dissipation rate
$\delta \theta $ in the streamwise direction, when strong dissipative events are either retained in or excluded from the measurement volume. In the present study, however, these events are related to maximum points of the scalar dissipation rate 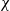 $\chi $ together with their local extent. When these regions are excluded from the scalar field, we observe a tendency of the probability density function
$\chi $ together with their local extent. When these regions are excluded from the scalar field, we observe a tendency of the probability density function 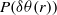 $P(\delta \theta (r))$ towards a Gaussian bell-shaped curve.
$P(\delta \theta (r))$ towards a Gaussian bell-shaped curve.