Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T12:31:11.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental and theoretical study of dewetting corner flow

Published online by Cambridge University Press:  03 December 2014

Hyoungsoo Kim ,
Christian Poelma ,
Gijs Ooms  and
Jerry Westerweel
Hyoungsoo Kim*
Affiliation:
Laboratory for Aero and Hydrodynamics, Delft University of Technology, Leeghwaterstraat 21, 2628 CA Delft, The Netherlands
Christian Poelma
Affiliation:
Laboratory for Aero and Hydrodynamics, Delft University of Technology, Leeghwaterstraat 21, 2628 CA Delft, The Netherlands
Gijs Ooms
Affiliation:
Laboratory for Aero and Hydrodynamics, Delft University of Technology, Leeghwaterstraat 21, 2628 CA Delft, The Netherlands
Jerry Westerweel
Affiliation:
Laboratory for Aero and Hydrodynamics, Delft University of Technology, Leeghwaterstraat 21, 2628 CA Delft, The Netherlands
*
†Present address: Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a partial dewetting corner flow with a moving contact line at a finite Reynolds number, 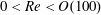$0<\mathit{Re}<O(100)$. When the speed of the moving contact line increases, the receding contact line appears with a corner shape that is also observed in a gravity-driven liquid droplet on an incline and on a plate withdrawn from a bath. In the current problem, 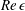$\mathit{Re}\,{\it\epsilon}$ is larger than unity, where ${\it\epsilon}$ is the aspect ratio of the flow structure. Therefore, classical lubrication theory is no longer appropriate. We develop a modified three-dimensional lubrication model for the dewetting corner structure at 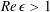$\mathit{Re}\,{\it\epsilon}>1$ by taking into account the internal flow pattern and by scaling arguments. The key requirement is that the streamlines in the corner are straight and (nearly) parallel. In this case, we can obtain a modified pressure consisting of the capillary pressure and the dynamic pressure. This model describes the three-dimensional dewetting corner structure at the rear of the moving droplets at 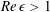$\mathit{Re}\,{\it\epsilon}>1$ and furthermore shows that the dynamic pressure effects become dominant at a small half-opening angle. Additionally, this model provides analytical results for the internal flow, which is a self-similar flow pattern. To validate the analytical results, we perform high-speed shadowgraphy and tomographic particle image velocimetry (PIV). We find a good agreement between the theoretical and the experimental results.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines Low-Reynolds-number flows: Lubrication theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 393 - 416
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2010 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Biance, A. L., Chevy, F., Clanet, C., Lagubeau, G. & Quéré, D. 2006 On the elasticity of an inertial liquid shock. J. Fluid Mech. 554, 47–66.CrossRefGoogle Scholar
Blake, T. D. 2006 The physics of moving wetting lines. J. Colloid Interface Sci. 299 (1), 1–13.CrossRefGoogle ScholarPubMed
Blake, T. D., De Coninck, J. & d’Ortona, U. 1995 Models of wetting: immiscible lattice Boltzmann automata versus molecular kinetic theory. Langmuir 11 (11), 4588–4592.CrossRefGoogle Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81 (2), 739–805.CrossRefGoogle Scholar
Brochard-Wyart, F. & De Gennes, P. G. 1992 Dynamics of partial wetting. Adv. Colloid Interface Sci. 39, 1–11.CrossRefGoogle Scholar
De Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863.CrossRefGoogle Scholar
De Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.CrossRefGoogle Scholar
Elsinga, G. E.2008 Tomographic particle image velocimetry and its application to turbulent boundary layers. PhD dissertation, Delft University of Technology, Delft (http://repository.tudelft.nl/file/1003861/379883).Google Scholar
Faber, T. E. 1995 Fluid Dynamics for Physicists. Cambridge University Press.CrossRefGoogle Scholar
Gentner, F., Ogonowski, G. & De Coninck, J. 2003 Forced wetting dynamics: a molecular dynamics study. Langmuir 19 (9), 3996–4003.CrossRefGoogle Scholar
Hancock, C., Lewis, E. & Moffatt, H. K. 1981 Effects of inertia in forced corner flows. J. Fluid Mech. 112, 315–327.CrossRefGoogle Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35 (1), 85–101.CrossRefGoogle Scholar
Kim, H., Große, S., Elsinga, G. E. & Westerweel, J. 2011 Full 3D-3C velocity measurement inside a liquid immersion droplet. Exp. Fluids 51 (2), 395–405.CrossRefGoogle Scholar
Kim, H., Westerweel, J. & Elsinga, G. E. 2013 Comparison of Tomo-PIV and 3D-PTV for microfluidic flows. Meas. Sci. Technol. 24 (2), 024007.CrossRefGoogle Scholar
Limat, L. & Stone, H. A. 2004 Three-dimensional lubrication model of a contact line corner singularity. Europhys. Lett. 65, 365–371.CrossRefGoogle Scholar
Mo, G. C. H., Liu, W. & Kwok, D. Y. 2005 Surface-ascension of discrete liquid drops via experimental reactive wetting and lattice Boltzmann simulation. Langmuir 21 (13), 5777–5782.CrossRefGoogle ScholarPubMed
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18 (1), 1–18.CrossRefGoogle Scholar
Mulkens, J., Flagello, D., Streefkerk, B. & Graeupner, P. 2004 Benefits and limitations of immersion lithography. J. Microlith., Microfab., Microsyst. 3, 104–114.Google Scholar
Owa, S. & Nagasaka, H. 2008 Immersion lithography: its history, current status and future prospects. Proc. SPIE 7140, 714015.CrossRefGoogle Scholar
Podgorski, T., Flesselles, J. M. & Limat, L. 2001 Corners, cusps, and pearls in running drops. Phys. Rev. Lett. 87, 36102.CrossRefGoogle ScholarPubMed
Reynolds, O. 1886 On the theory of lubrication and its application to Mr Beauchamp Tower’s experiments, including an experimental determination of the viscosity of olive oil. Proc. R. Soc. Lond. 40 (242–245), 191–203.Google Scholar
Reyssat, M., Pardo, F. & Quéré, D. 2009 Drops onto gradients of texture. Europhys. Lett. 87, 36003.CrossRefGoogle Scholar
Riepen, M., Evangelista, F. & Donders, S.2008 Contact line dynamics in immersion lithography-dynamic contact angle analysis. In Proceedings of 1st Euro. Conf. Microfluidics, Bologna, Italy, Societe Hydrotechnique de France (SHF).Google Scholar
Snoeijer, J. H., Rio, E., Le Grand, N. & Limat, L. 2005 Self-similar flow and contact line geometry at the rear of cornered drops. Phys. Fluids 17, 072101.CrossRefGoogle Scholar
Stone, H. A., Limat, L., Wilson, S. K., Flesselles, J. M. & Podgorski, T. 2002 Singularité anguleuse d’une ligne de contact en mouvement sur un substrat solide. C. R. Phys. 3 (1), 103–110.CrossRefGoogle Scholar
White, F. M. 2005 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Wieneke, B. 2008 Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45 (4), 549–556.CrossRefGoogle Scholar